掛け算の順序を違えてみたら、Rubyで驚くような違いが出た、という話をします。

交換法則と結合法則

実数や複素数の掛け算について、以下の2つの法則が成立します（わかりやすさのため、乗算記号も明示しています）。

交換法則：$a \times b = b \times a$
結合法則：$a \times (b \times c) = (a \times b) \times c$

算数教育の順序問題で話題になるのは交換法則の方ですが、今回は「結合法則」の方について考えてみます。

ということで、以下のようなものは今回考えません。

行列や四元数、キャラクターのカップリングなど、そもそも可換でない掛け算
文字列 * 整数や配列 * 整数（繰り返し）、配列 * 文字列（連結）など、数学的な乗算と別物になっているRubyの演算子

階乗の計算

いろいろあって、Rubyで階乗を計算することになりました。標準ライブラリにはないのですが、強力なEnumerableのおかげで、何も考えずに書いても1行で書けます。

def factorial(n)
  (1..n).reduce(&:*)
end

ただ、これは素朴なアルゴリズムなので、ある程度以上に個数が増えてくると、次第に遅くなってきます。Rubyの枠内でどうやって速くできるかなと考えてみたのですが、意外にシンプルな方法で想像以上に速くなりました。

分割統治

まずはコードを示します。

def factorial2(n)
  arr = [*1..n]
  loop do
    return arr[0] if arr.length == 1
    arr = arr.each_slice(2).map { |a, b| b ? a * b : a }
  end
end

each_sliceは見慣れないかもしれませんが、「指定された個数ごとにEnumerableから取り出す」というメソッドです（るりま）。あとは見ての通り、「隣同士の2個を取り出してかける」を1つになるまで、ひたすら繰り返すだけです（端数が出たときのために、ブロック内の? :があります）。

見た感じ、「かける順序を変えただけ」で、やることはほとんど変わっていないような気もするのですが、驚くほど違う結果が出ました（Windows10 x64、Core i7-6700という環境です）。

$ ruby -v
ruby 2.2.4p230 (2015-12-16 revision 53155) [x64-mingw32]

$ ruby factorial_speed.rb
                 user     system      total        real
Time for 100! (1000 times)
simple       0.031000   0.000000   0.031000 (  0.025863)
divided      0.016000   0.000000   0.016000 (  0.025553)

Time for 1000! (1000 times)
simple       0.531000   0.000000   0.531000 (  0.526687)
divided      0.235000   0.000000   0.235000 (  0.242633)

Time for 10000! (1000 times)
simple      30.500000   0.281000  30.781000 ( 30.778579)
divided      4.531000   0.031000   4.562000 (  4.556227)

Time for 20000! (1000 times)
simple     133.406000  11.985000 145.391000 (145.468692)
divided     12.110000   0.015000  12.125000 ( 12.138068)

20000の階乗を計算したときに至っては、10倍以上という信じがたいほどの速度差となっています。

乗算速度の検証

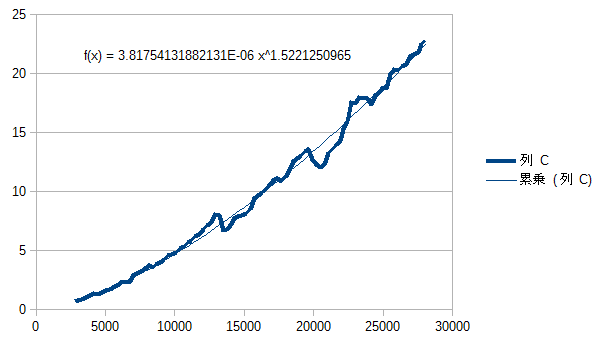
どうにも納得がいかなかったので、桁数を変えた場合のRubyの乗算速度について検証してみました。まずは、1違うだけでビット数は同じという数同士をかけて、速度を見てみました（横軸はビット数、縦軸は10万回あたりの秒数です）。

累乗で近似曲線を引いてみると、おおむね$O(n^{1.5})$となっていることがわかりました。そして、Rubyのソースを見てみると、計算法はKaratsuba法（$O(n^{1.585})$）とToom-3法（$O(n^{1.465})$）の組み合わせということで、その通りの結果だなという印象でした。

違う長さの数の場合

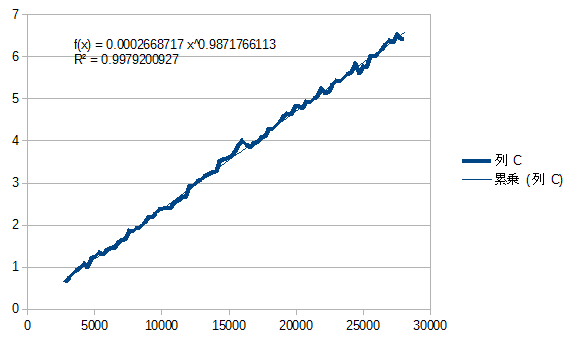
では、同じビット数ではなく、両者が違う場合はどのような挙動になるのでしょうか。まずは約2800ビット¹の数に、それより大きな数をかけてみます。この場合、おおむね大きい方の桁数に比例して時間が増加しています。

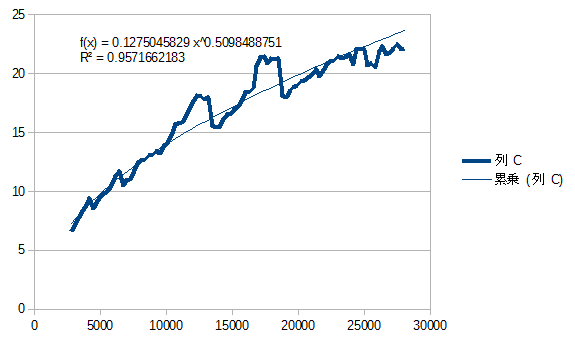
次に、約28000ビットの数に、それより小さな値をかけてみました。

少しガタついていますが、この場合はざっと小さい方の桁数の平方根に比例、という動きです。

コスト分析

*演算子にフックをしかけて、回数を記録させてみました。

hook.rb

$counts = Hash.new { |h, k| h[k] = 0 }
$enabled = false

module MultiplyHook
  def *(other)
    $counts[[size, other.size].sort] += 1 if $enabled
    super
  end
end

class Fixnum
  # hook multiply
  prepend MultiplyHook
end

class Bignum
  # hook multiply
  prepend MultiplyHook
end

このフックを仕掛けて階乗を計算させてみたところ、大きな数×Fixnumとなり続けるふつうの階乗に対して、小さな数同士で掛け算を行っている分割統治法、という違いがはっきりしました。そして、「大きい方の桁数×小さい方の桁数の平方根」として乗算にかかるコストを見積もってみたところ、1000!で、なんと50倍以上という差になりました。それだけ違いがあれば、配列の管理などを差し引いても分割統治法のほうが速くなってしまうわけです。

ソースコード

使用したコードについては、jkr2255/multiply_speedにアップしてあります。

2の累乗にすると最適化がかかりかねないので、7の累乗を使っていました。$7^{1000}$が約2800ビットです。 ↩

掛け算の順序問題 in Ruby