エクセル連番式いろいろ

エクセルで行連番を自動で振る式の書き方いろいろ
※以下、数式がセル番地に依存するものがあるため、基本的にセルA3から項番開始する前提で数式を記述します

1. ROW関数による行番号利用（マイナス値固定版）

数式

セルA3に

=ROW()-2

を書いて下にコピー。
※マイナスする値（-2部分）は、連番を開始する行-1の値を指定する

説明

ROW()関数で自身の行番号を取って、さらに連番開始行までの行数を引く。

問題点

• 項番開始前の行数が増減すると数式（-2部分）の書き換えが必要
• 縦に並んだ複数の表でそれぞれ連番を振る場合、表1と表2で異なる数式（-2部分）を記述する必要がある（表1で記述した数式のセルをそのままコピペで利用できない）

所感

連番の数式でよく見かける形。
式を書くのは簡単だけど、ヘッダ部分に行追加されたりして項番が2とかから始まっちゃっているのに誰も修正しないでそのままになっているのを寂しい目で眺めることが多いので、ほぼ自分では使わない。

2. ROW関数による行番号利用（マイナス値セル参照版）

数式

セルA3に

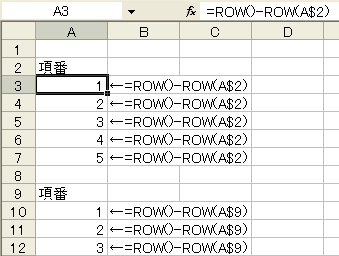
=ROW()-ROW(A$2)

を書いて下にコピー
※A$2部分は項番1となる行の前行セル番地を絶対行参照で指定する

説明

ROW()関数で自身の行番号を取って、さらに連番開始行の前行の行番号をROW()関数で取って引く。
マイナス値固定版と違い引く値を固定値でなくセル参照にしているため、連番開始前の行数増減時に連番がくずれる可能性を大幅に減らすことができる。

連番開始前の行数増減でくずれるパターン

上記画像イメージでいうところの

• 3行目に行追加
• 2行目を行削除

問題点

• 連番開始前の行数が増減すると、場合によって数式（A$2部分）の書き換えが必要
• 縦に並んだ複数の表でそれぞれ連番を振る場合、表1と表2で異なる式（A$2部分）を記述する必要がある（表1で記述した数式のセルをそのままコピペできない）

所感

上記行数増減でくずれるパターンについて、絶対参照するセルは表のヘッダ部分になると思うので、「2行目を行削除」という操作はほぼありえないんじゃないかと思う。
だが、「3行目に行追加」というのは表のヘッダを1行から2行に増やしたい等の意図でやる可能性が高い。
数式自体は簡単でそらで記述できるため、あまり頑張る必要も無くさらっと連番自動化を行いたいときは利用してもいいかもしれない。

3. 前行プラス1（前行セル参照版）

数式

セルA4に

=A3+1

を書いて下にコピー
※A3部分は自セル前行のセル番地を指定する

説明

前行のセル値にプラス1する。
項番1となる行は、前行が数値で無い場合は値のエラーになる。
しょうがないので項番1となるセルは数式で無く大胆に「1」と入力する。
※IF文等使って数式にできなくもないが、その他の問題（下記問題点参照）が多すぎて頑張る意味が無い

問題点

• 行削除で参照がくずれるので数式の再貼り付けが必要
• 行コピー＋行挿入で参照がくずれるので数式の再貼り付けが必要
• 行切り取り＋行挿入も言わずもがな

所感

こちらも連番の数式でよく見かける形。
だが、もう行削除や移動に耐えられない時点でいらっとくるので個人的には絶対使わない。例え障害表のように途中行の増減や行の入れ替えが無いような表であっても。
連番にこの数式を使うくらいなら数式を使わない（オートフィルで連番振って後は手作業でメンテする）ほうが皆に優しい。

4. 前行プラス1（OFFSET関数（自セル基準）版）

数式

セルA3に

=IF(TYPE(OFFSET(A3, -1, 0))=1, OFFSET(A3, -1, 0)+1, 1)

または

=N(OFFSET(A3, -1, 0))+1

を書いて下にコピー。
※A3部分は自セルのセル番地を指定する

説明

OFFSET()関数で自身の一つ上のセル値を取ってプラス1する。
かつ項番1となる行の前行が文字列等の場合エラーになるので、TYPE関数で数値かどうか判定するかN関数で数値変換する。
数式に含まれるセル参照は自身を指すため、行削除や挿入にいくらでも耐えることができる。
一度書いてしまえば、同一シートの別表や別シート、別ブックに至るまでセルコピー＋貼り付けでそのまま利用できる。

問題点

• 【IF+TYPE版】項番1となる行の前行が数値や日付形式の場合（TYPE関数で数値と判定されるものは全て不可）使い物にならない
• 【N関数版】項番1となる行の前行が数値や日付形式、TRUE（論理値）、エラー値の場合（N関数で0にならない値は全て不可）使い物にならない

備考：IF+TYPE版とN関数版について

IF+TYPE版とN関数版の違いは、N関数の方が判定がゆるいため、項番1となる行の前行の書式によって数式が機能しなくなる可能性が高くなる。
ただ、項番1となる行の前行は大抵文字列（"No."とか"項番"とか）になるはずなので、どちらを使ってもさして問題にならないと思う。
問題にならないのであればN関数の方が数式が短くなるのでお勧め。
※以降の前行プラス1版は全てN関数で記述します

所感

個人的によく使っていた。
ただ、連番式が必要になったときに以前書いた数式をセルコピーするべく「どのブックに書いたっけなぁ」と探すのが手間だったりする。
このページに書いた数式をコピペするにしても、セル番地により2箇所（A3部分）も編集しなければならない。

5. 前行プラス1（OFFSET関数（数式固定）版）

数式

項番開始するセル（項番1となるセル）に

=N(OFFSET(INDIRECT("A1"), ROW()-2, COLUMN()-1))+1

を書いて下にコピー。

説明

自セル基準版をベースに、どのセル番地でも数式が同一になる（＝上記数式をコピペでそのまま利用できる）ように改造した版。
OFFSET引数の「基準」はINDIRECTを利用して固定でA1を参照する。
INDIRECTにする理由は1行目やA列の行列追加削除で参照がずれないようにするため。
セルA1を基準に後は行数、列数にそれぞれROWとCOLUMNを駆使してA1から自セル前行のセルまでずらしている。
数式編集不要のため何も考えずに上記数式をコピペしてそのまま使える。

問題点

• 項番1となる行の前行が数値や日付形式、TRUE（論理値）、エラー値の場合（N関数で0にならない値は全て不可）使い物にならない

所感

数式を暗記したい場合は、後述のR1C1参照形式版の方が多少覚えやすいかも。

6. 前行プラス1（R1C1参照形式）

数式

項番開始するセル（項番1となるセル）に

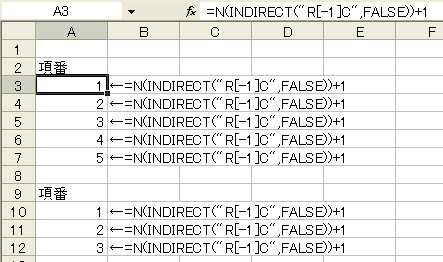
=N(INDIRECT("R[-1]C",FALSE))+1

を書いて下にコピー。

説明

前行をR1C1参照形式で参照してプラス1する。
通常はR1C1参照形式による参照は設定で無効になっているはずなので、INDIRECT関数で参照する。
数式編集不要のため何も考えずに上記数式をコピペしてそのまま使える。

問題点

• 項番1となる行の前行が数値や日付形式、TRUE（論理値）、エラー値の場合（N関数で0にならない値は全て不可）使い物にならない

所感

特になし。

まとめ

それぞれの数式のメリットデメリットわかりやすく表に、してみたら説明不足で逆によくわからない表になってしまったので以下参考程度に。

凡例：◎=良い　○=普通　×=悪い
※列ヘッダの番号は各見出し番号。

	1	2	3	4	5	6
表内行操作（削除・移動等）	◎	◎	×	◎	◎	◎
項番開始前の行数増減	×	○	◎	◎	◎	◎
数式編集不要	×	×	×	×	◎	◎
1シート内複数表	○	○	○	◎	◎	◎
列ヘッダ書式非依存	◎	◎	◎	○	○	○