この記事は
C++ Advent Calendar 2014 18日目の記事です。色々とネタに迷った結果、まだ日本語の解説記事が全然ないodeintを紹介することにします。(なぜこれほど日本語での解説が少ないのか。。)
Boost.Odeintとは
皆さんご存知Boostライブラリの1つで、常微分方程式を解くために使います。簡単にいうと
\frac{dx}{dt} = f(x,t)
という形をした方程式に対して使います。$x$は$t$に依存する変数、つまり$x=x(t)$ですね。これを解くアルゴリズムにはRunge-Kutta法(RK)やその改良版などがあります。Boost.OdeintはこのRK法を実装しています。GPGPUやMPI, OpenMPを利用した並列計算にも対応していますが、今回はそこまで説明しません。
いちばん簡単な方法
数値計算法に馴染みがない人も読むかもしれないので、上記の方程式を解くいちばん簡単な考え方を紹介します。そもそも「微分方程式を解く」というのはどういうことか?それは「任意の$t$を与えると、対応する$x$がわかる」ということです。ただし、上記の式中の関数$f$はわかっているものとします。また$t=0$での$x$も与えられているとします(多くの場合、$t$は時間を表すので初期条件といいます)。
まずは高校生で習った微分の定義に立ち戻ります。微分はこうでした。
\frac{dx}{dt} \equiv \lim_{\Delta t\to 0} \frac{x(t+\Delta t)-x(t)}{\Delta t}
数値計算上、$\Delta t$を無限小にすることはできませんが、十分小さな値にすることはできます。そうすると冒頭の式は近似的に、
\frac{x(t+\Delta t)-x(t)}{\Delta t} = f(x,t)
と書けます。これをちょっと変形してやると、
x(t+\Delta t) = x(t) + f(x,t) \Delta t
となりますね。この式に$t=0$を代入してやると、
x(\Delta t) = x(0) + f(x(0), 0) \Delta t
ここで初期条件、つまり$x(0)$は既知であること思い出してください。関数$f$はわかっていますので、この式の右辺はすべて求められ、左辺である$x(\Delta t)$がわかります。さらに、2つ上の式で$t=\Delta t$としてやると、
x(2\Delta t) = x(\Delta t) + f(x(\Delta t),\Delta t) \Delta t
が得られます。$x(\Delta t)$はすでに求められているので、$x(2\Delta t)$も求められます。以後同じように$x(3\Delta t), x(4\Delta t), ...$が求められますので任意の$t=n\Delta t$, ($n=0,1,..)$に対する$x$が得られます。つまり微分方程式が解けたということです。
この解き方は陽的オイラー法といいます。ここでいう陽的というのは、右辺に$x(t+\Delta t)$が現れていないという意味です。陽的というくらいですから、もちろん陰的解法もあります。陰的の場合には、近似式を
\frac{x(t+\Delta t)-x(t)}{\Delta t} = f(x(t+\Delta t),t)
とします。$x(t+\Delta t)$が両辺に現れてしまうので少し厄介になります。この記事では陰的解法については触れません。オイラー法は簡単ですが、あまり精度はよくありません。小さな$\Delta t$をとっても、$t$が大きくなるにつれ少しずつ誤差が増えていきます。そのため通常はより誤差が少ないRunge-Kutta法などを使います。
Odeintで使えるアルゴリズム
利用できるアルゴリズムの一覧はBoostドキュメントのOverviewにあります。OdeintではStepperと呼んでいるようです。どのStepperを使うべきかはケース・バイ・ケースと言う他ないのですが、まずはRunge-Kutta4から始めるといいかもしれません。Boost.OdeintのデフォルトはRunge-Kutta-Dopriのようです。
Runge-Kutta法(RK法)はとても有名なアルゴリズムで、大学で数値計算法の講義を受けるとほぼ必ず出てきます。このアルゴリズム、色々と改良版が開発されていましてRunge-Kutta-GillとかRunge-Kutta-Fehlberg(RKF)とかよく見ます。GillはBoost.Odeintにはないみたいですが、メモリ使用量が少なくて済むという記述をどこかの論文で見た気がします(要出典)。RKF法は刻み幅が誤差に応じて変化します。基本的なRK法は刻み幅が一定、つまり[0,1]の区間を100ステップで計算しようとすると0.01ずつ進んで行くのですが、RKF法だと無駄に小さすぎる刻み幅をとる必要がなくなるので優れものといえます。Boost.OdeintがデフォルトにしているRunge-Kutta-Dopriも刻み幅が変化します。しかも密出力(Dense Output)です。密出力というのは、刻み幅が大きくなった場合にその途中の値も補間して出してくれるということみたいです。精度がそこそこあり、刻み幅を変えることができて、密出力な点がデフォルトとされている理由のようです。他にも様々なRK法がOdeintには実装されているようです。
また、RK法以外にもいくつかアルゴリズムがあります。この記事で紹介した陽的オイラー法(Explicit Euler)や、Adams Bashforthが有名でしょうか。おそらく少し詳しい数値計算法の教科書では解説されていると思います。Boost.Odeintに用意されていないアルゴリズムでも、自分で実装することもできます。様々なアルゴリズムが共通のインターフェイスで扱えるようになるのはこのライブラリの強い利点ですね。
Odeintで解いてみる
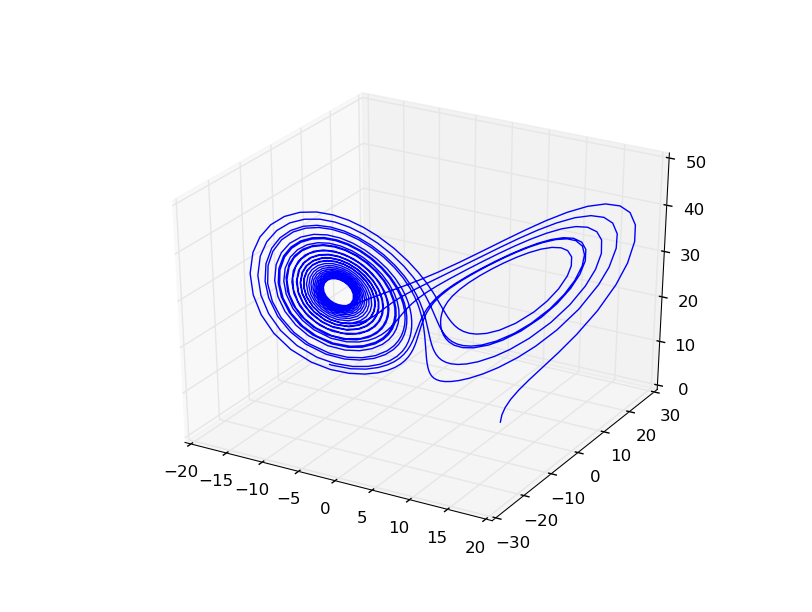
ローレンツ・アトラクタを例にOdeintを使って実際に解いてみます。ローレンツ・アトラクタについてはWikipediaなどに若干説明があります。「カオス的振る舞いをする」と書いてありますが、つまりは初期条件がわずかに変わると振る舞いが大きく変わる特徴を持ちます。私はこっち系の専門じゃないのでこの方程式について深い知識はありませんが、RK法のデモとしてはよく使います。Boost.OdeintのExampleにもありますが、ほぼ同じものを紹介します。
方程式
Wikipediaにもありますが、これです。$x,y,z$が位置座標、$t$が時刻と考えます。
\begin{align}
\frac{dx}{dt} &= -px+py \\
\frac{dy}{dt} &= -xz + rx - y \\
\frac{dz}{dt} &= xy-bz
\end{align}
式が3本あると思うかもしれませんが、ベクトル$\boldsymbol x = (x,y,z)$で書けばこうなります。
\frac{d\boldsymbol{x}}{dt} = f(\boldsymbol x)
$p$, $r$, $b$は定数なので右辺は関数$f$としてまとめてしまいました。今回は$f$は$t$に依存しません。
System
上記の方程式をC++で書きます。
# include<array>
using state_type = std::array<double,3>;
const double p = 10;
const double r = 28;
const double b = 8./3;
void lorenz_system(const state_type& x, state_type& dxdt, const double t)
{
// x=x[0], y=x[1], z=x[2]
dxdt[0] = -p*x[0] + p*x[1]; // dx/dt
dxdt[1] = -x[0]*x[2] + r*x[0] - x[1] ; // dy/dt
dxdt[2] = x[0]*x[1] - b*x[2]; // dz/dt
}
配列(ベクトル)を使ってるので$x$がx[0], $y$がx[1], $z$がx[2]という表記になりますが、方程式をそのまま書き表せています。Odeintではこのような方程式を表す関数をSystemと呼んでいます。ここまでできれば8割くらい完成したようなものです
Integrate
Boost.Odeintを使って方程式を解く部分を書き足します。Integrateは積分するという意味ですが、微分方程式を解く($x$を求める)というのは結局$x=\int \frac{dx}{dt} dt$を計算することなので、積分することと同じです。OdeintはデフォルトのStepperを使う便利な関数integrateを用意しています。
# include<array>
# include<boost/numeric/odeint.hpp> // 追加
using namespace boost::numeric::odeint; // 追加
using state_type = std::array<double,3>;
const double p = 10;
const double r = 28;
const double b = 8./3;
void lorenz_system(const state_type& x, state_type& dxdt, const double t)
{
// x=x[0], y=x[1], z=x[2]
dxdt[0] = -p*x[0] + p*x[1]; // dx/dt
dxdt[1] = -x[0]*x[2] + r*x[0] - x[1] ; // dy/dt
dxdt[2] = x[0]*x[1] - b*x[2]; // dz/dt
}
// main関数を追加
int main() {
state_type state0= { 10, 1, 1 };
integrate(lorenz_system, state0, 0., 25., 0.01);
return 0;
}
この通り簡単に書けます。integrate関数の引数の1番目にローレンツ・アトラクタのSystemを指定します。次の変数state0は初期条件
x(0)=10,\ y(0)=1,\ z(0)=1
です。3番目は初期時刻$t=0$、4番目は終了時刻$t=25$、5番目は刻み幅$dt=0.01$を指定します。単純に考えれば合計(25-0)/0.01=2500ステップ数ですが、integrate関数は刻み幅が一定ではないRunge-Kutta-Dopri法を使うので2500ステップにはなりません。実際には1000程度のステップ数になります。
以上で計算そのものはできたことになります。
計算結果を見る
計算しても結果が見えてなくては意味がありません。まずは上記のソースコードを、計算結果を出力できるように修正します。
# include<iostream> // ☆
# include<fstream> // ☆
# include<array>
# include<boost/numeric/odeint.hpp>
using namespace boost::numeric::odeint;
using state_type = std::array<double,3>;
const double p = 10;
const double r = 28;
const double b = 8./3;
void lorenz_system(const state_type& x, state_type& dxdt, const double t)
{
// x=x[0], y=x[1], z=x[2]
dxdt[0] = -p*x[0] + p*x[1]; // dx/dt
dxdt[1] = -x[0]*x[2] + r*x[0] - x[1] ; // dy/dt
dxdt[2] = x[0]*x[1] - b*x[2]; // dz/dt
}
int main() {
std::vector<double> timelog; // ☆
std::vector<state_type> statelog; // ☆
state_type state0= { 10, 1, 1 };
integrate(lorenz_system, state0, 0., 25., 0.01,
[&](const state_type& state, const double t) // ☆
{
timelog.push_back(t);
statelog.push_back(state);
}
);
// ☆ バイナリで出力
std::ofstream ofs("lorenz.dat",std::ios::binary);
const size_t N = timelog.size();
ofs.write(reinterpret_cast<const char*>(&N), sizeof(N));
ofs.write(reinterpret_cast<char*>(&timelog[0]), sizeof(double)*N);
ofs.write(reinterpret_cast<char*>(&statelog[0]),sizeof(state_type)*N);
return 0;
}
変更した箇所に☆をつけてみました。
integrateにラムダ式を追加しています。いわゆるObserverというやつです。これで時刻$t$とそのときのベクトル$\boldsymbol x$を記録できます。もちろんstd::coutを使うこともできますが、私は計算結果を標準出力に出すのは好きじゃないので。。微分方程式を解いた後、テキストデータではなくバイナリデータで直接出しています。図を出すときに結局Pythonを使うのでテキストでもバイナリでも手間に大した違いはないです。
データをファイルに出せたので、後は図にするだけです。C++でグラフを描くいいライブラリはないのでPythonでやります。後処理までC++を使っていては時間の無駄です。みんなPython使いましょう。グラフ出すスクリプトはこれです!
# !/usr/bin/env python3
import pylab as pl
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
with open("lorenz.dat") as fd:
N, = np.fromfile(fd, np.dtype("i8"), 1)
dtype = np.dtype("{N}f8,({N},3)f8".format(N=N))
(time,state), = np.fromfile(fd, dtype, 1)
x,y,z = [ state[:,i] for i in range(3) ]
fig = pl.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x,y,z)
pl.show()
Python...なんて簡単なんでしょう...
凝った例も出すつもりでしたが、なんか忙しいのでこの辺でやめます。よいお年を。
次は、@mrk_21さんです。