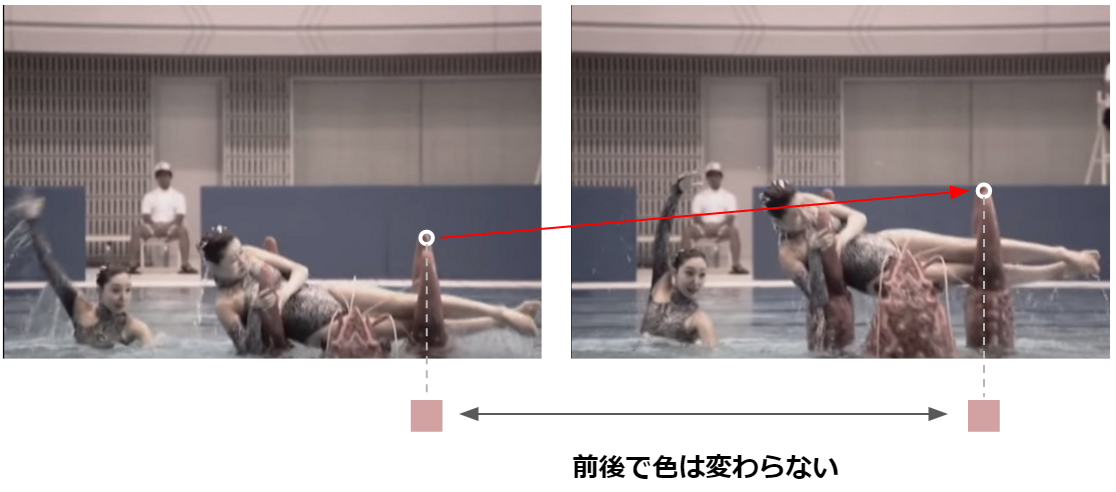
ザリガニに挟まれて持ち上げられるなんてことがたまにあると思いますが、そんな時どれだけ激しい動きだったのか解析したい!なんてこともあるんじゃないでしょうか。

出典: ASIAN KUNG-FU GENERATION 『君の街まで』 (ソルファ リメイク記念)
そうした(?)、画像間の動きを表現したものがOptical Flowです。Optical Flowは、2つの画像間で各点がどう動いたのかを表現します。これを計算することで、↑の図のように画像上の特徴点の動きを解析したりすることが可能になります。
本稿では、そのOptical Flowを計算するための理論的な背景と、Python/OpenCVを使った実装までを紹介していきたいと思います。
Optical Flowの位置づけ
画像間の動きの解析については、様々な目的とそれを実現する手法があります。ここでは、まずOptical Flowがその中でどのような位置づけになるのか説明しておきます。
- トラッキング
- 目的: 画像の中の特定の物体(人やオブジェクト)を追跡したい
- 手法: リアルタイムに行うものとそうでないものの、大別して2種類
- ->リアルタイム型: テンプレートマッチングやMean Shiftなど、ターゲットオブジェクトを様々な手法で表現し画像フレーム間での追跡を行う。
- ->バッチ型: すべての画像が出そろった後で、動的計画法などで動きを逆算する
- フロー推定
- 目的: 画像の中で何がどう動いたのかを検知したい(観測対象が決まっているトラッキングとは異なる)
- 手法: 画像の中の特徴的な点に絞って解析するsparse型と、画素全体の動きを解析するdense型に大別できる
- -> sparse型: Lucas–Kanade法など
- -> dense型: Horn–Schunck法、Gunnar Farneback法など
実際にはフロー推定の手法がトラッキングで使われたりなど分類の垣根はあいまいですし、使っている手法で分けることもあるので若干混沌としてる感はありますが、だいたいこんな形で分けられます。
そして、今回ご紹介するOptical Flowはその名前の通りフロー推定になります。
理論編
では、どうやってOptical Flowを計算していくのかについて、その理論的な内容を解説していきます。
パラパラ漫画を想像するとわかりやすいですが、動画とはつまるところ連続した画像になります。
そのため、2つの画像間の動きを解析することができれば、それをつなげていき動画全体の動きを明らかにすることができそうです。
では、2つの画像があったとき、その間の動きはどうすれば推定できるでしょうか。
動きがあるということは、画像上のある点が別の点に移動しているということです。逆に言うと位置以外(色など)が変わってしまうともう追跡のしようがないので、2つの画像間で色(処理時はグレースケールに変換することが多いので、「明度」)は同じはず、という前提を置きます。
ここから数式が出てきますが、一つずつ進んでいくので安心してください。
ある時刻$t$における、画像$I$上の点$x, y$の明度を$I(x, y, t)$とします。時刻が$\Delta t$だけ進み、その間に座標が$\Delta x, \Delta y$動いたとすると、移動先の明度は$I(x + \Delta x, y + \Delta y, t + \Delta t)$となります。
これらは変わってないはず、という仮定を先ほど置いたので以下の等式が成り立ちます。
$$I(x, y, t) = I(x + \Delta x, y + \Delta y, t + \Delta t)$$
この方程式から、最終的には単位時間当たりの座標の変化量である$\frac{\Delta x}{\Delta t}, \frac{\Delta y}{\Delta t}$を導くのが今から行う計算のゴールになります。
まずは、テイラー展開を使い右辺を近似します。テイラー展開というと何かものすごく難しい技を使っている気がしますが、単に本当の値に近い値になるよう変形しているだけです。簡単な解説はこちらをご参照ください。
$$
I(x + \Delta x, y + \Delta y, t + \Delta t) = I(x, y, t) + \frac{\partial I}{\partial x} \Delta x + \frac{\partial I}{\partial y} \Delta y + \frac{\partial I}{\partial t} \Delta t + ...
$$
このあとずっと続いていくのですが、続いていくにつれてどんどん微小な値になっていくので、思い切ってバッサリ切り捨てて最初の展開だけにしてしまいます。
$$
I(x + \Delta x, y + \Delta y, t + \Delta t) = I(x, y, t) + \frac{\partial I}{\partial x} \Delta x + \frac{\partial I}{\partial y} \Delta y + \frac{\partial I}{\partial t} \Delta t
$$
そうするとどうなるかというと、以下のようになります。
$$
I(x, y, t) = I(x + \Delta x, y + \Delta y, t + \Delta t) = I(x, y, t) + \frac{\partial I}{\partial x} \Delta x + \frac{\partial I}{\partial y} \Delta y + \frac{\partial I}{\partial t} \Delta t
$$
こうすると$\frac{\partial I}{\partial x} \Delta x + \frac{\partial I}{\partial y} \Delta y + \frac{\partial I}{\partial t} \Delta t = 0$でないと等式が成り立たなくなってしまうので、これらは0ということにします。
この式を$\Delta t$、つまり時間の変化量で割ると、以下のようになります。
$$
\frac{\partial I}{\partial x} \frac{\Delta x}{\Delta t} + \frac{\partial I}{\partial y} \frac{\Delta y}{{\Delta t}} + \frac{\partial I}{\partial t} = 0
$$
簡素化のため、$\frac{\partial I}{\partial x} = I_x$という風に表記すると、以下のようになります。
$$I_x \frac{\Delta x}{\Delta t} + I_y \frac{\Delta y}{{\Delta t}} + I_t = 0 $$
ようやく$\frac{\Delta x}{\Delta t}, \frac{\Delta y}{{\Delta t}}$が出てきました。この$x, y$それぞれの単位時間当たりの移動量をベクトル$\bf{v}$という形でまとめると、最終的に以下の式を解けばよいことになります。
$$
I_x {\bf v_x} + I_y {\bf v_y} + I_t = 0 \\
\nabla I^T {\bf v} = - I_t
$$
ただ、結論から言うとこのままではこの式は解けません。ここまで数式を頑張って追ってきたのになんやねん!となってしまいますが、${\bf v_x}$、${\bf v_y}$と2つの未知数がある(2次元)のに対して方程式は一つしかないのでこれは仕方ないのです。Optical Flowを求める際に直面するこの問題をAperture Problem(窓問題)と言います(なぜそう言うのか、というのは説明が長くなるわりに結局ほかの制約が必要だよね、という以上のことは何も言っていないので、ここでは割愛します)。
さて、この状況を解決するには、少なくとも一つ以上制約となる方程式を増やす必要があります。これが本題で、動きを検出する様々な手法はこの「制約」をどうかけるのかが主要なテーマとなっており、様々なアイデアが提案されています。
ここでは、sparse型の代表格であるLucas–Kanade法と、dense型の手法としてHorn–Schunck法の2つを紹介しようと思います。
Lucas–Kanade法
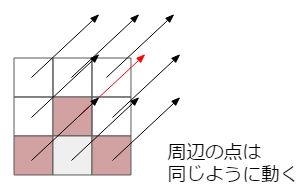
Lucas–Kanade法では、空間的整合性を仮定し制約をかけます。要は、周辺の点は同じ動きをするはずだ、と仮定するということです。
周辺の点を$q_1 ... q_n$とし、これらがすべて同様の動きをする、と仮定すると以下のように制約式を水増しできます。
$$
I_x(q_1) {\bf v_x} + I_y(q_1) {\bf v_y} = - I_t(q_1) \\
I_x(q_2) {\bf v_x} + I_y(q_2) {\bf v_y} = - I_t(q_2) \\
... \\
I_x(q_n) {\bf v_x} + I_y(q_n) {\bf v_y} = - I_t(q_n) \\
$$
ここで各項を以下のように行列でまとめます。
$$
A = \left[
\begin{array}{cc}
I_x(q_1) & I_y(q_1) \\
I_x(q_2) & I_y(q_2) \\
\vdots & \vdots \\
I_x(q_n) & I_y(q_n)
\end{array}
\right]
\
b = \left[
\begin{array}{c}
- I_t(q_1) \\
- I_t(q_2) \\
\vdots \\ - I_t(q_1)
\end{array}
\right]
$$
そうすると、以下のようにシンプルに書けます。
$$
A{\bf v} = b
$$
あとはこの連立方程式を解くだけです。これは最小二乗法を使って解くことができ(端的には$||b - A{\bf v}||^2$で表現できる二乗誤差が最小となるポイントを、微分を利用し見つける)、最終的には以下のように表せます。
$$
{\bf v} = (A^TA)^{-1} A^Tb
$$
この式が解けるには式が示す通り$A^TA$に逆行列が存在すること(可逆であること)が前提になりますが、特徴点検出の代表的な手法であるHarrisコーナー検知やShi-Tomasi検知で検出できる点では成立します。
Horn–Schunck法
Horn–Schunck法では、移動の「滑らかさ」について制約をかけます。要は、最短距離で移動しているものほどよい${\bf v}$とするということです。
移動にかかるコスト(エネルギー)を$E({\bf v})$とし、それを以下のように定義します。これはコストなので、小さいほど良いということになります。
$$
E({\bf v}) = E_{data}({\bf v}) + \alpha E_{smooth}({\bf v})
$$
ここで、$E_{data}({\bf v})$は今手元にある一つ目の方程式を表現します。前述のとおり$I_x {\bf v_x} + I_y {\bf v_y} + I_t$は0になるはずなので、これが0に近いほど良い${\bf v}$となります。以下では画像全体について足し合わせるために積分をとっています。
$$
E_{data}({\bf v}) = \int\int (I_x {\bf v_x} + I_y {\bf v_y} + I_t) ^2 dxdy
$$
そして、$E_{smooth}({\bf v})$が「滑らかさ」に関する制約になります。
$$
E_{smooth}({\bf v}) = \int\int || \nabla {\bf v_x} || ^2 + || \nabla {\bf v_y} || ^2 dxdy
$$
これは${\bf v}$の変化量が小さいほど良い、つまり「明度が変わらない点へ、小さな変化量でたどり着けている」ものほど良いということになります。$\alpha$は、この滑らかさの制約にどれくらい重きを置くかという係数になります。
この式を最小化問題として解くことで、目的の${\bf v}$が得られることになります。以後の解くための展開は割愛しますが、これがHorn–Schunck法の考え方になります。
実践編
では、実際にOpenCVを使ってOptical Flowの検出を実装してみたいと思います。ここでは、実装が提供されているLucas–Kanade法とGunnar Farneback法を使います。Gunnar Farneback法はdense型のよく利用される手法です(制約はLucas–Kanade法と同様近隣の点を利用している・・・はず)。
実際に実装したサンプルは以下に置いてありますが、ここからは著作権的な問題から素材としてNHKのCREATIVE LIBRARYにあるどーもくんを使用しています。
icoxfog417/cv_tutorial/opticalflow
Python3.5、numpy1.10.4、OpenCV3.1.0を使っています(Anaconda/Minicondaを使うと楽です)。ただ、Matplotlibだけひとつ前の1.4.3を使っています。これは2016/4現在、最新版の1.5.1でアニメーション再生のために使っているnbaggの実行にバグがあるためです(notebook backend figures close spontaneously #6075)。
実装については、基本はOpenCVのチュートリアルの通りです。まずはLucas–Kanade法から。
走ってますね。。。その軌跡が追跡できていることがわかるかと思います。
Lucas–Kanade法では特徴点の検出を行い、その周辺の点からOptical flowを推定します。よって、肝となる処理は以下の二点です。
- 特徴点検出: goodFeaturesToTrack
- Optical Flowの算出: calcOpticalFlowPyrLK
特徴点は、当然検出されない可能性もあるので注意してください(検出できなかった場合、Noneが返されます)。それと、途中から動画にカットインしてくるようなものは検出が行われませんでした。追跡するものは最初から映っている必要があるので、その点ご注意ください(色々試してみましたが、なぜかは不明)。
Gunnar Farneback法により密なOptical Flowを求めると、以下のような感じでより動き全体をとらえることができます。
余談ですが、動画の読み込みに使用しているVideoCaptureは、画像ファイルも渡すことができます。例えば、img_%02d.jpgと指定すると自動的にimg_01.jpg、img_02.jpg・・・と連番のファイルを読み込んでくれます。これで簡単にパラパラ漫画が作れるので、試してみるのも一興です。
解説は以上となります。皆さんも思い出に残る躍動をとらえてみてください!
参考文献
- 定量生物学の会チュートリアル 画像情報学研究者は何をやっているのか?
- 超大作の資料。Optical Flow以外についても丁寧に書かれていてわかりやすい
- 画像メディア工学特論(5)
- [Computer Vision Advent Calendar 2012] LucasKanade法の導出及び特徴について
- Introduction to OpenCV
- Optical Flow I/ Guido Gerig CS 6320, Spring 2012
- Wikipedia(実はかなりわかりやすい)
- Optical_flow
- Lucas–Kanade method
- Horn–Schunck method
- OpenCV-Python Tutorials/Optical Flow
- 電子情報通信学会『知識の森』 4 章 動画解析
- 初心者用 テイラー展開解説 - 東北工業大学
- OPTFLOW_USE_INITIAL_FLOW option for cvCalculateOpticalFlowFarneback
- Dense Optical Flow Expansion Based On Polynomial Basis Approximation