@gg_hatano さんの素晴らしいブログ記事がある。
私は野球は全く分からないのですが、結論として気になることが書いてあります。
大島は3位でした。ただ、打席数は多いです。
セカンドゴロ製造機と認定してよさそうです。
この意味をちょっと考えてみようと思います。
3位でもいいんですか?
結局大島は、セカンドゴロの割合は 3 位でした。
しかし、セカンドゴロ製造機と認定していいそうです。
その理由は、大島は他のバッターに比べて打席数が多いからだそうです。
これはどういうことでしょうか?
例えば 3 打席中 1 回ヒットを打った打者 A と、100 打席中 30 回ヒットを打った打者 B とでは、どちらが優秀かを考えてみて下さい。
打率だけで見ると、打者 A は 0.33、打者 B は 0.3 と、打者 A の方が勝っています。
しかし、3 回中 1 回ヒットを打っただけで、3 割バッターと呼んでいいのでしょうか?
1 回のヒットは、単なるまぐれ当たりかもしれません。
つまり、打席数が少ないと、打率を計算したとき、その値は信頼できないということです。
逆に、打席数が多いほど、打率の値は信頼できるようになる、ということです。
今回、大島の打席数は多いので、セカンドゴロの割合の値は他の打者より信頼できるため、セカンドゴロ製造機として認定してよい、ということです。
信頼区間
統計学では、このように計算した値がどのくらい信頼できるのかを「信頼区間」によって表します。
実際に上記ブログのデータを使って信頼区間を計算してみましょう。
まずは上記ブログからデータを取ってきます。
library(XML)
data <- readHTMLTable("http://gg-hogehoge.hatenablog.com/entry/2015/10/31/210811", header = TRUE, which = 2, encoding="utf-8")
data <- setNames(data, iconv(colnames(data), "utf-8", "sjis"))
knitr::kable(data)
| チーム | 選手 | 結果 | 回数 | 打数 | 割合 | |
|---|---|---|---|---|---|---|
| 1 | ロッテ | 岡田 幸文 | 二ゴロ | 30 | 208 | 0.1442 |
| 2 | ソフトバンク | 髙谷 裕亮 | 二ゴロ | 29 | 208 | 0.1394 |
| 3 | 中日 | 大島 洋平 | 二ゴロ | 84 | 608 | 0.1382 |
| 4 | 楽天 | 後藤 光尊 | 二ゴロ | 58 | 440 | 0.1318 |
| 5 | 巨人 | アンダーソン | 二ゴロ | 35 | 269 | 0.1301 |
| 6 | 楽天 | 藤田 一也 | 二ゴロ | 57 | 447 | 0.1275 |
| 7 | 巨人 | 立岡 宗一郎 | 二ゴロ | 50 | 397 | 0.1259 |
| 8 | 中日 | 森野 将彦 | 二ゴロ | 31 | 248 | 0.1250 |
| 9 | 楽天 | 銀次 | 二ゴロ | 41 | 354 | 0.1158 |
| 10 | ヤクルト | 雄平 | 二ゴロ | 71 | 616 | 0.1153 |
ここでは、セカンドゴロの発生モデルとして二項分布を仮定します。
二項分布の比率の信頼区間は binom パッケージによって計算できます。
binom::binom.exact() 関数によって、信頼区間の上限と下限を求めます。
library(dplyr)
library(binom)
result <- data %>%
group_by(`選手`) %>%
do(binom = binom.exact(.$`回数`, .$`打数`)) %>%
summarise(`選手`, `回数`=binom$x, `打数`=binom$"n",
`下限`=binom$lower, `割合`=binom$"mean", `上限`=binom$upper) %>%
arrange(desc(`割合`))
knitr::kable(result, digits = 3)
| 選手 | 回数 | 打数 | 下限 | 割合 | 上限 |
|---|---|---|---|---|---|
| 岡田 幸文 | 30 | 207 | 0.100 | 0.145 | 0.200 |
| 髙谷 裕亮 | 29 | 208 | 0.095 | 0.139 | 0.194 |
| 大島 洋平 | 84 | 608 | 0.112 | 0.138 | 0.168 |
| 後藤 光尊 | 58 | 439 | 0.102 | 0.132 | 0.167 |
| アンダーソン | 35 | 269 | 0.092 | 0.130 | 0.176 |
| 藤田 一也 | 57 | 447 | 0.098 | 0.128 | 0.162 |
| 立岡 宗一郎 | 50 | 395 | 0.095 | 0.127 | 0.163 |
| 森野 将彦 | 31 | 248 | 0.087 | 0.125 | 0.173 |
| 銀次 | 41 | 354 | 0.084 | 0.116 | 0.154 |
| 駿太 | 44 | 381 | 0.085 | 0.115 | 0.152 |
このままではちょっとわかりにくいので、可視化します。
library(ggplot2)
ggplot(result, aes(x=`選手`, y=`割合`)) +
geom_point() +
geom_errorbar(aes(ymin=`下限`, ymax=`上限`)) +
scale_x_discrete(limits=result %>% arrange(`割合`) %>% .$`選手`) +
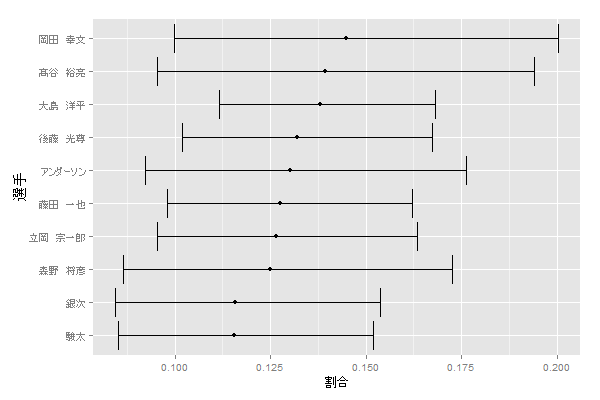
coord_flip()
大島のセカンドゴロ率は、3 位ですが、上位二人に比べて信頼区間が非常に狭く、信頼できる値であることがわかります。
さらに
上図は、セカンドゴロ率の大きい順に並べていますが、今度は信頼区間の下限の大きい順に並べてみましょう。
ggplot(result, aes(x=`選手`, y=`割合`)) +
geom_point() +
geom_errorbar(aes(ymin=`下限`, ymax=`上限`)) +
scale_x_discrete(limits=result %>% arrange(`下限`) %>% .$`選手`) +
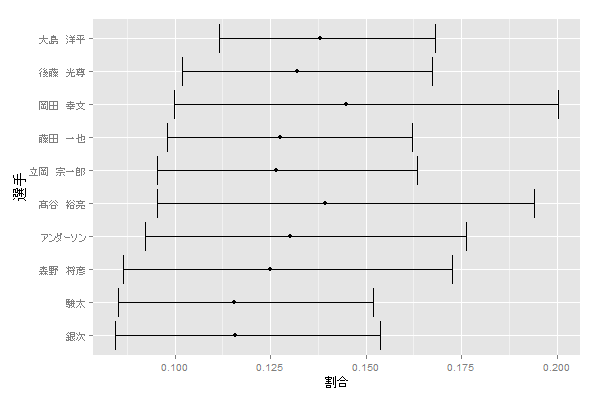
coord_flip()
信頼区間の下限で並べると、大島がトップに来ます。
信頼区間の下限は、セカンドゴロ率は最低でもこのぐらいはあるよ、という目安になるので、大島のセカンドゴロ率の高さは揺るぎないものであることがわかります。
一方、信頼区間の上限で並び替えると、次のようになります。
ggplot(result, aes(x=`選手`, y=`割合`)) +
geom_point() +
geom_errorbar(aes(ymin=`下限`, ymax=`上限`)) +
scale_x_discrete(limits=result %>% arrange(`上限`) %>% .$`選手`) +
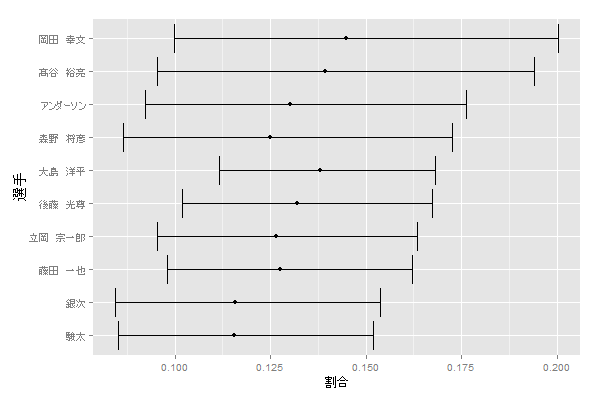
coord_flip()
今度はロッテの岡田がトップになりました。
信頼区間の上限は、セカンドゴロ率は最高でここぐらいまで上がるよ、という目安になります。
つまり、ロッテの岡田はセカンドゴロ製造機となるポテンシャルが最も高い男だということです。
ロッテの監督は彼の打席をもっと増やしてみて、セカンドゴロの量産に挑戦してみてはいかがでしょうか?
Enjoy!