ｔ分布は正規分布とカイ二乗分布で作れる #rstatsj

統計学入門(p.202)より

二つの確率変数 $Y$ と $Z$ が次の条件を満たすものとする。
(a) $Z$ は標準正規分布 $N(0,1)$ に従う。
(b) $Y$ は自由度 $k$ の $\chi^2$ 分布 $\chi^2(k)$ に従う。
(c) $Z$ と $Y$ は独立である。
いま、確率変数 $t$ を
$$t = \frac{Z}{\sqrt{Y/k}}$$
と定義すると、$t$ が従う確率分布を自由度 $k$ の $t$ 分布(あるいは、スチューデントの $t$ 分布)という。

したがって、次のようにすれば $t$ 分布からの乱数を発生させることができる。

R

N <- 10000
k <- 2

random_from_norm <- rnorm(N, mean = 0, sd = 1)
random_from_chisq <- rchisq(N, df = k)
my_random <- random_from_norm / sqrt(random_from_chisq/k)

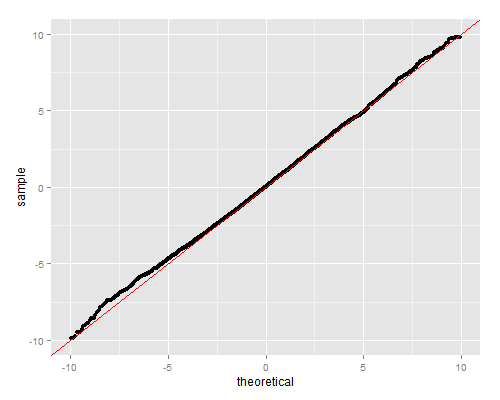
これが $t$ 分布と一致することを、qq プロットで確認してみよう。

R

library(ggplot2)

qplot(sample=my_random, dist=qt, dparams = list(df = k)) +
  geom_abline(intercept=0, slope=1, color="red") +
  xlim(-10, 10) + ylim(-10, 10)

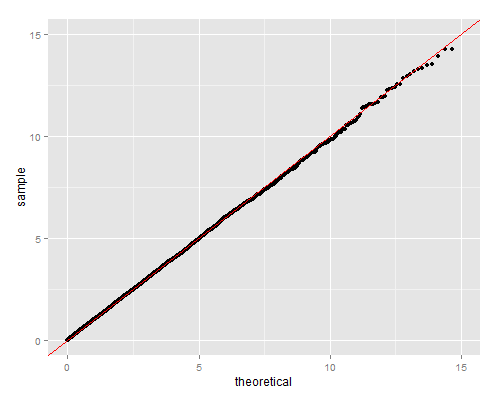
ちなみに

カイ二乗分布は正規分布から作れる。

R

my_chisq <- Reduce("+", replicate(k, list(rnorm(N)^2)))

qplot(sample=my_chisq, dist=qchisq, dparams = list(df = k)) +
  geom_abline(intercept=0, slope=1, color="red") +
  xlim(0, 15) + ylim(0, 15)

あとはわかるな？

Enjoy!