#はじめに
冬休みにThetaの360°画像にぼかしを入れるWebアプリSphereBlur.comを作った際に、どのように360°写真を表示するのか悩んだ。編集ツールなので、引いた画面ではできるだけ広い範囲を表示したいが、単純に球体にテクスチャを貼り付けて、透視投影や平行投影をしても半球までしか表示できない。いろいろ悩んでいたら、どこかで見たこの絵
を思い出して、おおっ！これだっ！って思ったけど、後で調べたらTHETAのAndroid/iOSアプリの表示はミラーボール投影というものらしい・・・VR業界では常識なのかな？
#テクスチャを使ったミラーボール投影
というわけで、three.jsのこのサンプルを参考にしてミラーボールの環境マッピングを試してみた。しかしこの場合、ポリゴンで構成された球、つまり多面体で反射した景色なので、ズームして回転した際にどうしても歪みが気になってしまう。そこで、自前でWebGLのフラグメントシェーダを書いてみることにした。
#デモ
https://horo-t.github.io/tmp/20151225/mirror_ball_view.html
#計算
ミラーボール反射はどうやって計算するのか考えてみる。
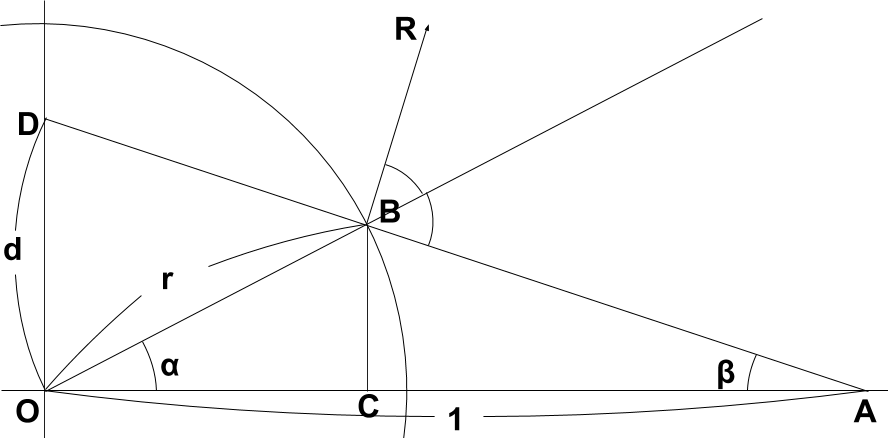
図のように原点Oと視点Aの距離を$OA=1$と固定し、ミラーボールの半径をrとした場合を考え、原点Oからdの距離にある点Dとし、$\overrightarrow{AD}$方向の視線にどの方向からの光が反射するか($\overrightarrow{BR}$)を求めるために、まず$\alpha$を求める。
CB:OD=CA:OA
なので、
\begin{align}
\frac{CB}{OD}&=\frac{CA}{OA}\\
\frac{r \sin{\alpha}}{d}&=\frac{1-r\cos{\alpha}}{1}\\
r\sin{\alpha} + rd\cos{\alpha}&=d\\
\frac{1}{\sqrt{1+d^2}}\sin{\alpha}+\frac{d}{\sqrt{1+d^2}}\cos{\alpha}&=\frac{d}{r\sqrt{1+d^2}}\\
\cos{\beta}\sin{\alpha}+\sin{\beta}\cos{\alpha}&=\frac{d}{r\sqrt{1+d^2}}\\
\sin{(\alpha+\beta)}&=\frac{d}{r\sqrt{1+d^2}}\\
\cos{(\alpha+\beta)}&=\frac{\sqrt{r^2+r^2d^2-d^2}}{r\sqrt{1+d^2}}
\end{align}
ここから$\sin{\alpha}$、$\cos{\alpha}$を求めると、
\begin{align}
\sin{\alpha}&=\sin{(\alpha+\beta-\beta)}\\
&=\sin{(\alpha+\beta)}\cos{\beta}-\cos{(\alpha+\beta)}\sin{\beta}\\
&=\frac{d}{r\sqrt{1+d^2}}\frac{1}{\sqrt{1+d^2}}-\frac{\sqrt{r^2+r^2d^2-d^2}}{r\sqrt{1+d^2}}\frac{d}{\sqrt{1+d^2}}\\
&=\frac{d(1-\sqrt{r^2+r^2d^2-d^2})}{r(1+d^2)}\\
\cos{\alpha}&=\cos{(\alpha+\beta-\beta)}\\
&=\cos{(\alpha+\beta)}\cos{\beta}+\sin{(\alpha+\beta)}\sin{\beta}\\
&=\frac{\sqrt{r^2+r^2d^2-d^2}}{r\sqrt{1+d^2}}\frac{1}{\sqrt{1+d^2}}+\frac{d}{r\sqrt{1+d^2}}\frac{d}{\sqrt{1+d^2}}\\
&=\frac{\sqrt{r^2+r^2d^2-d^2}+d^2}{r(1+d^2)}
\end{align}
$\alpha$の値が求まると、後は簡単で、求めたい方向$\frac{\overrightarrow{BR}}{|BR|}$は、法線ベクトル$\frac{\overrightarrow{OB}}{|OB|}$に対する$\frac{\overrightarrow{AB}}{|AB|}$の反射なので、
\frac{\overrightarrow{BR}}{|BR|}=\frac{\overrightarrow{AB}}{|AB|}-2(\frac{\overrightarrow{AB}}{|AB|}\cdot\frac{\overrightarrow{OB}}{|OB|})\frac{\overrightarrow{OB}}{|OB|}
で求めることができる。