Go to Qiita Advent Calendar 2024 Top
LoginSignup
348
261

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

Machine LearningAdvent Calendar 2016

Day 10
@horiem(horiem)in株式会社RICOS (RICOS Co. Ltd.)

PCAとSVDの関連について

Last updated at Posted at 2016-12-10

この記事は、Machine Learning Advent Calendar 2016 10日目の記事です。

次元削減や統計分析によく使われる PCA （主成分分析：principal component analysis）と SVD （特異値分解：singular value decomposition）の関連について書いていきます。というか、ぶっちゃけ（次元削減をするという目的では）どっちもほぼ同じようなものですよ、というのが主張です。

記事の作成にあたって、 Cross Validated の amoeba 氏の回答を大いに参考にさせていただきました。また、扱っているトピックの性質から、線形代数と統計学の基礎的な知識を前提としています。

まずはなぜ次元削減をしたいのか？ をざっと説明し、そのあと数学的に PCA と SVD の関連性について見ていきます。最後に、Python を用いて数学的な部分を補足します。

なぜ次元削減をしたいのか？

例として、製品の長さ、幅、重さから製造所を学習して、新しい製品を持ってきたときにその製造所を予測する、というような問題が考えられます。

長さ 幅 重さ $\cdots$ 製造所ID
3.0 5.1 100.2 $\cdots$ A
2.9 5.3 100.1 $\cdots$ A
3.4 5.2 98.2 $\cdots$ B
2.9 4.8 101.0 $\cdots$ C
$\vdots$ $\vdots$ $\vdots$ $\vdots$ $\vdots$

この場合、長さ、幅、重さ……などの測定値を 特徴量 、製造所IDを ラベル として何らかの機械学習をすることが考えられます。ただ、多くの場合、この特徴量が多すぎるといった状況が発生します。中には、「製造に要した時間」のようなおおよそ関係なさそうな測定値が入っていたり、重さと体積のような、明らかに相関がありそうなものが入っていたりします。

人間であれば「この特徴量は関係なさそうだな」とあらかじめアタリをつけて表から落としたりもできますが、基本的に機械学習アルゴリズムは与えられた特徴量を公平に評価します。その結果、ラベルと論理的に関係がない特徴量にまで相関を見出してしまう……なんてことも起こってしまいます。

また、特徴量どうしに相関がある場合、それらのモデル内での役割はほぼ同じであり、そこまで多くの情報を持っていることにはなりません。極端な例を挙げると、「長さ」のカラムが表に2つあってまったく同じ値が入っていたら、どちらかはいらないデータですよね。カラムが2つあるように見えても、実質的にはカラム1つ分の情報しかないわけです。

こういった「いらない特徴量」があると学習に時間がかかるだけでなく、ノイズになったり過学習を引き起こしたりとあまりいいことはありません。そこで登場するのが 次元削減 という考え方で、書いて字のごとく、特徴量の次元（=個数）を削減してしまおうというもので、PCA や SVD なども次元削減に活用されています。

PCA の数学的表現

データとして、サイズ $[n \times p]$ の行列 $X$ を考えます（$n > p$）。ここで、 $n$ がデータの点数、 $p$ が特徴量の数であり、各データは標準化（分散を $1$、平均をゼロにする操作）されているとします。すると、 サイズ $[p \times p]$ の（不偏）共分散行列 $\Sigma$ は、

\Sigma = \frac{X^T X}{n - 1}

と書けます（平均を引き忘れているように見えますが、平均をゼロとする操作をすでにしているので、不要です）。

ここで、共分散行列を固有値分解することによって、

\begin{align}
\Sigma &= V_{pca} L V^T_{pca}
\\
V_{pca} &= \left( \begin{array}{cccc}
\boldsymbol{v_1} & \boldsymbol{v_2} & \cdots & \boldsymbol{v_p}
\end{array} \right)
\\
L &= \left( \begin{array}{cccc}
\lambda_1 & 0 & 0 & \cdots & 0
\\
0 & \lambda_2 & 0 & \cdots & 0
\\
\vdots & & \ddots & & \vdots
\\
\\
0 & 0 & & \cdots & \lambda_p
\end{array} \right)
\end{align}

が得られます。

ここで、$\lambda_i$ は $i$ 番目の固有値（固有値は大きい順に並んでいるとします）、 $\boldsymbol{v_i}$ は対応する固有ベクトルで、 $p$ 次元の列ベクトルです。PCA の場合特に $\boldsymbol{v}_i$ のことを 第 $i$ 主成分 と呼びます。

また、$V_{pca}$ 、$L$ の行列のサイズはどちらも $[p \times p]$ で、$V_{pca}$ は直交行列です。

もとのデータを主成分の空間に変換したい場合は、 $X V_{pca}$ とします。また、$V_{pca}$ の最初の $k$ 列（$k \lt p$）だけをとってきた $[p \times k]$ 行列 $V_{pca}^{(k)}$ を使うことによって、 $X V_{pca}^{(k)}$ と、 $p$ 次元から $k$ 次元へ次元削減することができます。

SVD の数学的表現

同じデータ行列 $X$ を考えます。詳細は省略しますが、SVD を行うことによって、

\begin{align}
X &= U S V_{svd}^T
\\
S &= \left( \begin{array}
 \ s_1 & 0 & 0 & \cdots & 0
\\
0 & s_2 & 0 & \cdots & 0
\\
\vdots & & \ddots & & \vdots
\\
\\
0 & 0 & & \cdots & s_p
\\
0 & 0 & & \cdots & 0
\\
0 & 0 & & \cdots & 0
\\
\vdots & \vdots & & & \vdots
\end{array} \right)
\end{align}

というような分解ができます。ここで、 $U$ と $V_{svd}$ はそれぞれサイズ $[n \times n]$ 、 $[p \times p]$ の直行行列で、$S$ のサイズは $[n \times p]$ です。また、この $s_i$ のことを 特異値 と呼びます。

PCA のときと同様に、 $X V_{svd}$ とすることで変換ができ、 $X V_{svd}^{(k)}$ で次元削減ができます。

PCA と SVD のつながり

ここまでで出てきた重要な式をもう一度書いておきます。

\begin{align}
\Sigma &= \frac{X^T X}{n - 1}
\\
\Sigma &= V_{pca} L V_{pca}^T
\\
X &= U S V_{svd}^T
\end{align}

$X$ が SVD によって分解できることがわかっているので、これを 1 番目の式に代入してみましょう。

\begin{align}
\Sigma &= \frac{X^T X}{n - 1} &
\\
&= \left( U S V_{svd}^T \right) ^T U S V_{svd}^T \ / \ (n - 1)&
\\
&= V_{svd} S^T U^T U S V_{svd}^T \ / \ (n - 1) &
\\
&= V_{svd} S^T S V_{svd}^T \ / \ (n - 1) & (\because 直交行列の性質より、 U^T U = 1)
\end{align}

一方、PCA から $\Sigma = V_{pca} L V_{pca}^T$ だったので、見比べると

V_{pca} L V_{pca}^T = \frac{V_{svd} S^T S V_{svd}^T}{n - 1}

となります。PCA と SVD の関連が見えてきそうですね！

固有値の関連

$S^T S$ の部分を計算してみると、

S^T S = \left( \begin{array}{cccc}
s_1^2 & 0 & 0 & \cdots & 0
\\
0 & s_2^2 & 0 & \cdots & 0
\\
\vdots & & \ddots & & \vdots
\\
\\
0 & 0 & & \cdots & s_p^2
\end{array} \right)

と、対角行列になってくれます。ここから、

\lambda_i = \frac{s_i^2}{n - 1}

がわかります1。なんと、主成分に対応する固有値と特異値の間に、こんなシンプルな関係があったんですね。

主成分の関連

では、固有値の関連を考慮に入れて先ほどの関連の式を見てみましょう。

\begin{align}
V_{pca} L V_{pca}^T &= \frac{V_{svd} S^T S V_{svd}^T}{n - 1} &
\\
V_{pca} L V_{pca}^T &= V_{svd} L V_{svd}^T & (\because 固有値の関連)
\end{align}

ここから、 $V_{pca}$ と $V_{svd}$ はかなり近いものだということが予想されます。直感的には $V_{pca} = V_{svd}$ としたくなりますが（そしてそれは正しい場合もありますが）、正しくありません。SVD において $V_{svd}$ は一意に決まらない場合があるためです。

この部分に関しては、実際にコードで確認してみましょう。

Python での検証

サンプルコード

では、 Python3 で検証していきましょう。ポイントとしては、

  • 行列の掛け算に ＠ 演算子（＝ np.dot()）を使用（* だと要素対要素の積になってしまう）
  • sklearn のPCA ライブラリでは母集団分散をベースにしているので不使用
  • 固有ベクトルが固有値の大きさ順に並んでないないのでソート
  • SVD ででてくる $V_{svd}$ が転置されているので、数式との整合性を考えてさらに転置

という感じです。

import numpy as np
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

# Define data
X = np.array([[1, 2],
              [2, 4],
              [3, 6],
              [4, 8]], dtype=float)
n, p = X.shape

# Standardize the data
stdsc = StandardScaler()
X_std = stdsc.fit_transform(X)

# Perform PCA
cov = X_std.T @ X_std / (n - 1)
W, V_pca = np.linalg.eig(cov)
# Sort eigenvectors with eigenvalues
index = W.argsort()[::-1]
W = W[index]
V_pca = V_pca[:, index]

# Perform SVD
U, s, V_svd = np.linalg.svd(X_std, full_matrices=True)
V_svd = V_svd.T
S = np.zeros((n, p))
S[:p, :p] = np.diag(s)

# Print results
print("Engenvalues from PCA")
print(W)
print("Eigenvalues from SVD")
print(s ** 2 / (n - 1))

print("V_pca")
print(V_pca)
print("V_svd")
print(V_svd)

# Plot results
X_pca = X_std @ V_pca[:, :2]
X_svd = X_std @ V_svd[:, :2]

plt.scatter(X_std[:, 0], X_std[:, 1], color='red')
plt.scatter(X_pca[:, 0], X_pca[:, 1], marker='+', color='blue')
plt.scatter(X_svd[:, 0], X_svd[:, 1], marker='o', color='green')
plt.show()

特徴量に完全な相関があるとき

インプットにはとりあえず、1つめの特徴量と2つめの特徴量が完全に相関しているときを置いてみます。

出力はこちら。

Engenvalues from PCA
[ 2.66666667  0.        ]
Eigenvalues from SVD
[  2.66666667e+00   2.15722070e-32]
V_pca
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]
V_svd
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]

まずは固有値の比較から、 $\lambda_i = s_i^2 \ / \ (n - 1)$ の式が正しいことを確認してください。また、この場合は $V_{pca}$ と $V_{svd}$ が等しくなっていそうです。

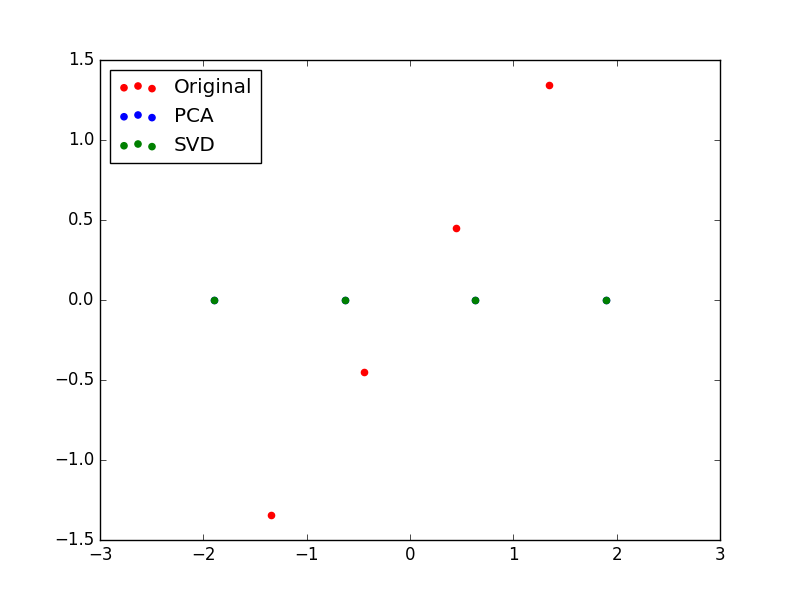
また、元のデータの1列めと2列めのプロット、第一主成分と第二主成分のプロット（サンプル後半部分）はこちら。

figure_1.png

赤が元データで、ひとつめの特徴量とふたつめの特徴量が完全に相関していることが見て取れると思います。これはインプット通りですね。

緑（その下に青もありますが、隠れています）が、$V_{pca}$ や $V_{svd}$ で変換した後のデータです。

見てわかる通り、第1主成分だけが残り、第2主成分はすべてゼロになってしまいました。これは、冒頭の方で書いた、「『長さ』のカラムが表に2つあってまったく同じ値が入っていたら〜」の再現です。完全に相関している2つの特徴量は、実質的に特徴量1つ分の情報しか持っていないということですね。

特徴量に完全な相関がないとき

では、入力データを

X = np.array([[1, 2],
              [2, 5],
              [3, 6],
              [4, 7]], dtype=float)

のように変えてみましょう。特徴量の相関を完全ではなくします。

Engenvalues from PCA
[ 2.60824385  0.05842282]
Eigenvalues from SVD
[ 2.60824385  0.05842282]
V_pca
[[ 0.70710678 -0.70710678]
 [ 0.70710678  0.70710678]]
V_svd
[[ 0.70710678  0.70710678]
 [ 0.70710678 -0.70710678]]

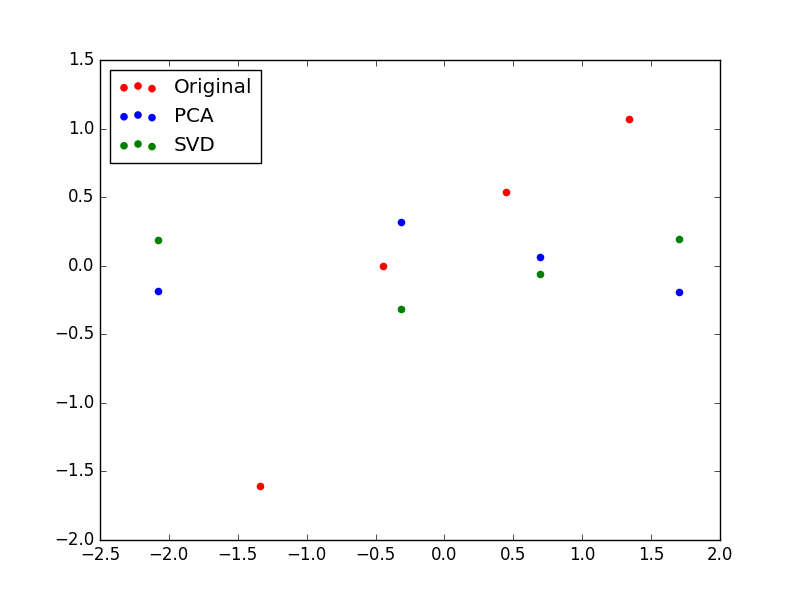
今度は、$V_{pca} と $V_{svd}$ で第2主成分（2 列目）の符号が違っています。これが、先ほど言っていた、ふたつが一致しない状況、ということですね。ただ、符号が違うだけなので、軸としては同じものを表しているようなイメージですね。

figure_2.png

データのプロットを見ると、今度は第2主成分も非ゼロの値を持ちます。今度は特徴量同士の相関が完全ではなかったため、相関でカバーできなかった部分（＝新しい情報）が第2主成分でカバーされているというわけです。

また、第2主成分の方向が PCA と SVD で異なっていたために、データがちょうど $X$ 軸対象になっています。

次元削減をするとき

では、データを3次元に増やして

X = np.array([[1, 5, 4],
              [2, 4, 3],
              [3, 5, 2],
              [4, 0, 0]], dtype=float)

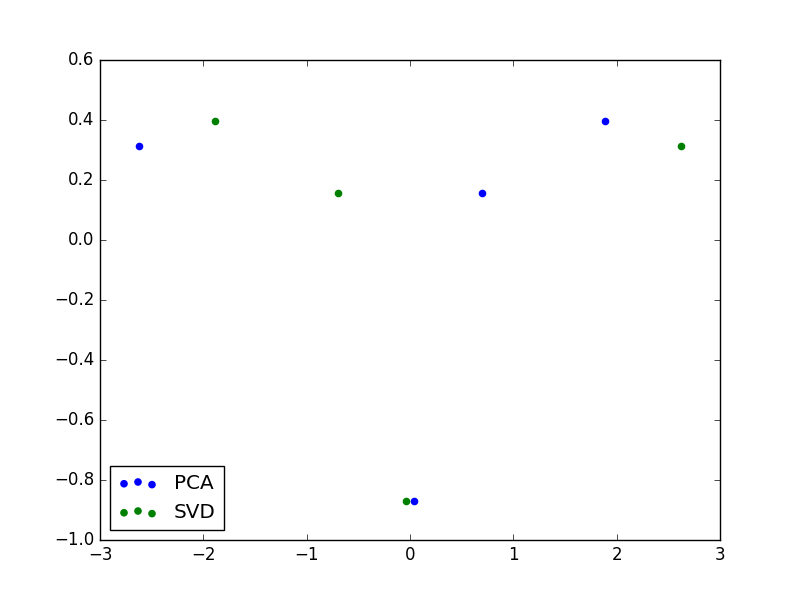
として計算しました。PCA と SVD で得られた第1、第2主成分だけをプロットしています。つまり、3次元から2次元に次元削減をしたようなイメージです。

このときは第1主成分の符号が逆転していたので、 $Y$ 軸対称のデータになっています。しかし、この対称な違いを除いて、このふたつは同じ情報を持っています。

figure_3.png

まとめ

PCA と SVD、ふたつの対応関係を見てきました。

  • 共分散行列の固有値と特異値にはシンプルな対応がある
  • 主成分は、符号を除いて同じ
  • 次元削減の結果で得られるデータも、符号を除いて同じ

では、このふたつのうちどちらを使うのが望ましいでしょうか？

個人的に、イメージがつかみやすいのは PCA です。なので、何か理論的なことを考えるときにはPCA を使うと見通しがいい場合が多いと思います。

ただし、Mathematics Stack Exchange のJ. M.氏の回答によると、SVD のほうが数値的に安定しているようです。実際、そこで挙げられている Läuchli matrix に対しては、 SVD のほうが良い結果を出しているようです。

  1. $V_{svd}$ は規格化された直交ベクトルの並びなので、勝手に係数をかけることができません。なので、$1 / (n - 1)$ の部分は必ず $S^T S$ の部分にかかっているだろうと判断できるわけです。 ↩

348
261
4

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
348
261

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?