はじめに
こんにちは.先日,
という記事を読んで
バッチ正規化使ってないなら人生損してるで
If you aren't using batch normalization you should
とあったので,TheanoによるBatch Normalizationの実装と検証(?)を行ってみました.
- [Survey]Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
を一部参考にしています.
Batch Normalization
アルゴリズム
バッチごとに平均が0,分散が1になるように正規化行います.
$B$をmini-batchのとある入力の集合,$m$をbatch sizeとすると,
B = \{x_{1...m}\}\\
以下で,$\epsilon$は安定化のためのパラメータだそうです.
\epsilon = 10^{-5}\\
\mu_{B} \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_i\\
\sigma^2_{B} \leftarrow \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu_{B})^2\\
\hat{x_i} \leftarrow \frac{x_i - \mu_{B}}{\sqrt{\sigma^2_{B} + \epsilon}}\\
y_i \leftarrow \gamma \hat{x_i} + \beta
上式について,$\gamma$と$\beta$がパラメータでそれぞれ正規化された値をScaling及びShiftするためのものだそうです.それぞれ,誤差逆伝播法で学習する必要があるのですが,ここでは詳しい式の導出を割愛します.
Fully-Connected Layerの場合
通常のFully-Connected Layerでは入力次元分だけ平均,分散を計算する必要があります.
つまり,入力のshapeが(BacthSize, 784)の場合,784個の平均,分散を計算する必要があります.
Convolutional Layerの場合
一方,Convolutional Layerでは,channel数ぶんだけ平均,分散を計算する必要があります.
つまり,入力のshapeが(BatchSize, 64(channel数), 32, 32)の場合,64個の平均,分散を計算する必要があります.
メリット
Batch Normalizationのメリットとしては,大きな学習係数を設定でき,学習を加速させることができるようです.
Theanoによる実装
class BatchNormalizationLayer(object):
def __init__(self, input, shape=None):
self.shape = shape
if len(shape) == 2: # for fully connnected
gamma = theano.shared(value=np.ones(shape[1], dtype=theano.config.floatX), name="gamma", borrow=True)
beta = theano.shared(value=np.zeros(shape[1], dtype=theano.config.floatX), name="beta", borrow=True)
mean = input.mean((0,), keepdims=True)
var = input.var((0,), keepdims=True)
elif len(shape) == 4: # for cnn
gamma = theano.shared(value=np.ones(shape[1:], dtype=theano.config.floatX), name="gamma", borrow=True)
beta = theano.shared(value=np.zeros(shape[1:], dtype=theano.config.floatX), name="beta", borrow=True)
mean = input.mean((0,2,3), keepdims=True)
var = input.var((0,2,3), keepdims=True)
mean = self.change_shape(mean)
var = self.change_shape(var)
self.params = [gamma, beta]
self.output = gamma * (input - mean) / T.sqrt(var + 1e-5) + beta
def change_shape(self, vec):
ret = T.repeat(vec, self.shape[2]*self.shape[3])
ret = ret.reshape(self.shape[1:])
return ret
使い方の例(ほとんど擬似コード)は,
...
input = previous_layer.output #シンボル変数,前の層の出力,shape=(batchsize, 784)
h = BatchNormalizationLayer(input, shape=(batchsize, 784))
# activationする場合
h.output = activation(h.output) # activation=何らかの活性化関数
...
params = ... + h.params + ... # ネットワークのパラメータ,更新の時に使う.
実験
実験設定
データはMNISTを使い,単純な多層ニューラルネットワークで実験しました.
- 中間層の数:10
- 中間層の各ユニット数:全部784
- 最適化手法:シンプルなSGD(学習係数:0.01)
- 活性化関数:tanh
- Dropout Ratio:中間層1層目は0.1,それと入出力層以外は0.5
- Batch Size:100
- 誤差関数:Negative Log Likelihood
まぁ
入力層→(Fully-Connected Layer→Batch Normalization Layer→Activation)*10→出力層
みたいな感じです.
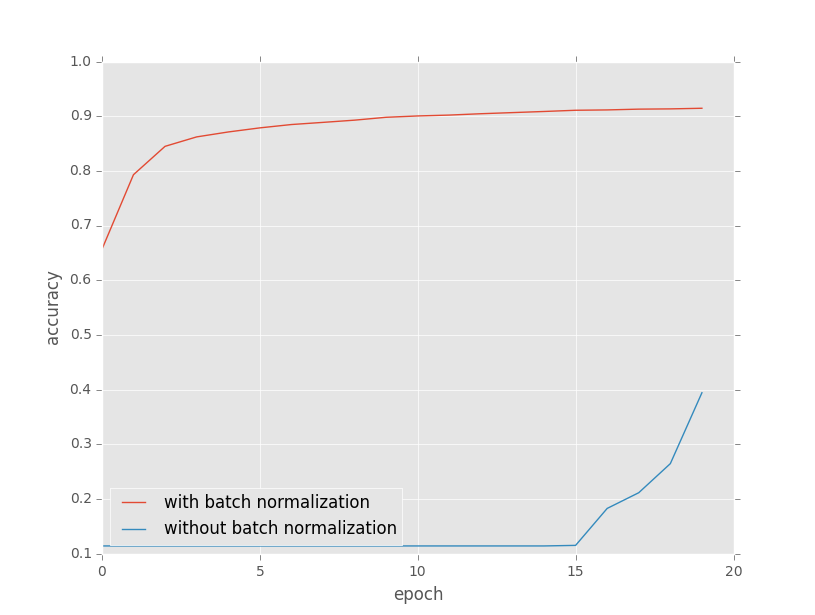
実験結果
最後に
実験設定にちょっと無理があったかもしれないですけど,Batch Normalization使わないと損ってことがわかったかもしれません.