はじめに
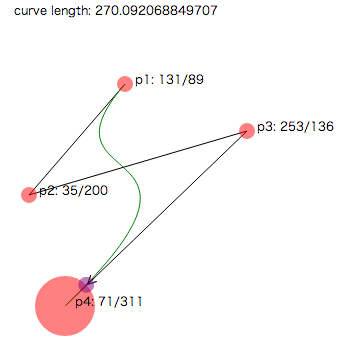
下図のように円に向けてベジェ曲線を引くときに、綺麗に中心に向くようにしたいので、ベジェ曲線の終点を円の中心にした場合にマーカを円の外周上に置きたいという希望があります。
で、2つ案を考えましたが、どちらもイマイチだと判明したという自分用メモです。
図1. まあまあ良い例
デモ
ベジェ曲線のp1, p2, p3, p4はドラッグ可能です。
矢印の配置案
1. refXに円の半径をプラス
refXについては下記をご参照ください。
refXに円の半径をプラスするのはお手軽で良いかと思ったのですが、図2のようなベジェ曲線だとイマイチでした。refXはベジェ曲線の端点での接線方向に進むので、曲線上から外れてしまうんですね。
図2. refXでオフセット指定だと位置がずれる例
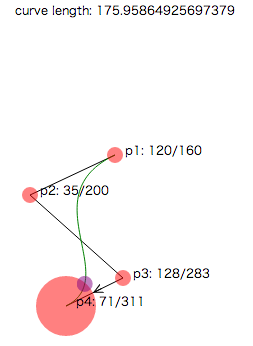
2. ベジェ曲線の線上で端点から円の半径だけ戻った点に置く
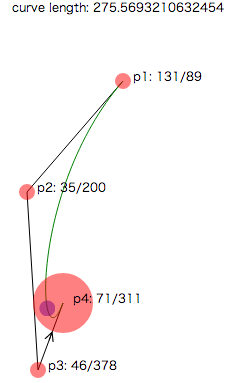
上の図では紫色の円の中心がその点です。図1、図2ではよさそうですが、図3のようなベジェ曲線だと円の中に埋もれてしまいます。
図3. 端点からの一定距離に配置するのでもダメな例
考察
ベジェ曲線と円の外周の交点に矢印を配置するのがよさそうです。
ただ、それにしても実際に図を書くときにわざわざ図3のように曲線を引き回すのはしないほうがよいと思います。交点上で曲線の接線方向に矢印を向けても、見た目はイマイチだと思うので。
デモのコード解説
参考資料
この記事のデモコードは下記のサイトのコードをJavaScriptに移植してリファクタリングしたものです。
-
A Primer on Bézier Curves
- ベジェ曲線について様々な値を計算する方法について実に詳しく解説している神サイトです。
- しかもサンプルコードはPublic Domainだそうです。
-
Moving Along a Curve with Specified Speed
- ベジェ曲線上で指定の距離の点のパラメータを逆算する手法が紹介されています
ベジェ曲線の線の長さの計算
SVGのSVGPathElementにもgetTotalLengthやgetPointAtLengthやgetPathSegAtLengthなどの関数は用意されています。が、指定した距離での曲線パラメータを取得する関数が無いなど、必要な機能に対して不足しています。
また、OSX上のFirefoxだとgetTotalLengthの結果が正しくなかったりFirefoxがハングしたりします。1044355 – SVG path getTotalLength hangs for some path with two cubic bezier segments
ということで、線の長さも結局自前で計算する必要が出てきます。
この記事のデモではA Primer on Bézier CurvesのArc lengthに書かれた手法を使ってベジェ曲線の長さを計算しています。
通常ならベジェ曲線の微分ベクトルの長さを数値積分する必要があるのですが、ここではGauss quadratureという近似法を使うことで数値積分を回避して比較的少ない計算量で済んでいます。
ベジェ曲線の指定した距離に対応する曲線パラメータを計算
A Primer on Bézier CurvesのTracing a curve at fixed distance intervalsでは点線を引く用途ということもあり、曲線パラメータtを一定間隔で線長sを計算し、sからtの逆引きテーブルを作ってルックアップするという手法を採用しています。
ですが、今回は曲線の終端から一定距離の曲線パラメータtが欲しかったので、Tracing a curve at fixed distance intervalsからリンクされているMoving Along a Curve with Specified Speedの手法を使いました。
"3.1 Numerical Solution: Inverting an Integral."と"3.2 Numerical Solution: Solving a Differential Equation"の2つの手法が紹介されていたのですが、後者は分母が0に近い場合は問題があるとの事だったので、前者の手法を採用しました。
今後の方向性
A Primer on Bézier CurvesのIntersectionsに曲線と曲線の交点を求める手法が解説されているので、これを使ってベジェ曲線と円の外周の交点を求めたいところです。
また、d3.jsでUMLのクラス図用の矢印を作ってみた - Qiitaではマーカに曲線が被らないようにstroke-dasharrayで調節していましたが、Splitting curvesに指定の曲線パラメータでベジェ曲線を分割する方法が解説されていたので、これを使ってベジェ曲線を円の外周との交点からマーカの幅分離れたところで分割すれば、stroke-dasharrayを使わなくても良さそうな気がします。