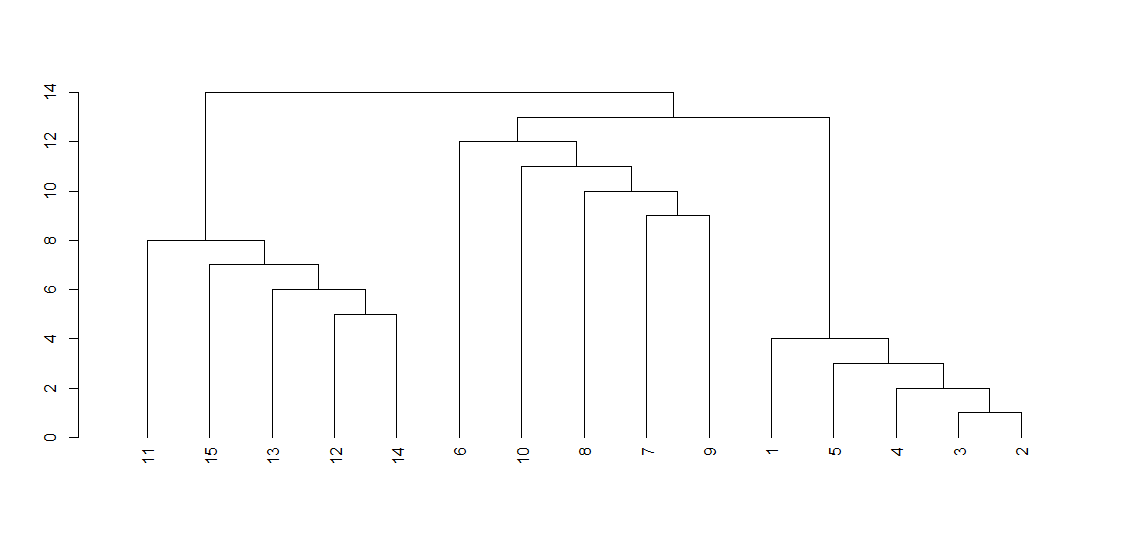Rでネットワーク解析をする(Introduction)
ネットワーク解析のツール
Pythonのライブラリにnetworkxというものがあります。
すごいですよ。
ネットワーク解析用で、ダイクストラアルゴリズムなどが実装されています。
グラフの描画では、きれいに描画できるものにGephiがあります。
今回は、Rのライブラリigraphを使って解析をしたいと思います。
初期設定
クラスタリングなどのネットワーク解析をRでするために、以下のライブラリを使用します。
クラスタリングは、分野によってはコミュニティ検出ともいわれているようです。
> sessionInfo() # Rのバージョン情報です
## R version 3.0.2 (2013-09-25)
## Platform: i386-w64-mingw32/i386 (32-bit)
##
## locale:
## [1] LC_COLLATE=Japanese_Japan.932 LC_CTYPE=Japanese_Japan.932
## [3] LC_MONETARY=Japanese_Japan.932 LC_NUMERIC=C
## [5] LC_TIME=Japanese_Japan.932
##
## attached base packages:
## [1] stats graphics grDevices utils datasets methods base
##
## other attached packages:
## [1] knitr_1.4.1
##
## loaded via a namespace (and not attached):
## [1] digest_0.6.3 evaluate_0.4.7 formatR_0.9 stringr_0.6.2
## [5] tools_3.0.2
> install.packages(”igraph”) # ミラーは適宜選択
> library(igraph) # install.packages(”igraph”) を実行した後に実行する
グラフデータの用意
igraphには、txtファイルやGraphML(ノードやエッジのあるグラフを表現するファイル形式でXMLの文法を用いたものです)でデータを読み込ませることもできます。
今回はRのクラスタリングの例ですので、以下のサンプルデータを使ってやってみます。
このデータはクラスタリングがあからさまなデータとなっています。
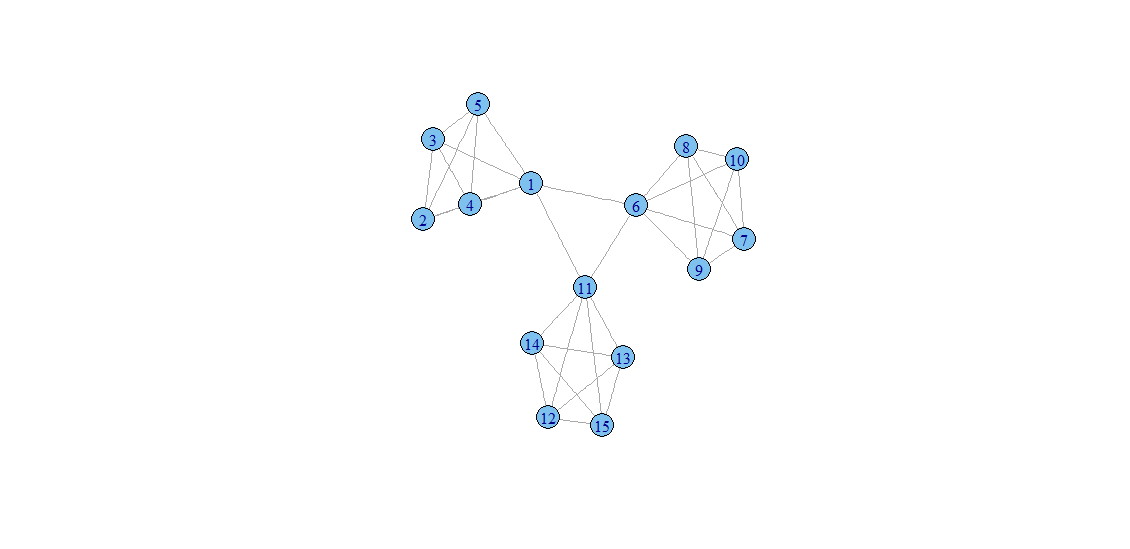
# サンプルデータの用意
> g.sample <- graph.full(5) %du% graph.full(5) %du% graph.full(5) # 完全グラフを3つ作る
> g.sample <- add.edges(g.sample, c(1, 6, 1, 11, 6, 11)) # ノード1,6間、1,11間、6,11間にエッジを追加する
> plot(g.sample, layout = layout.lgl) # プロットする
Modularity が最大になる分割を求める
グラフのクラスタリングの出来具合(精度)を測る指標として Modularity "Q" というものがあります。
他にもありますが、今回はこれを使ったクラスタリングを試したいと思います。
使用するアルゴリズムによって、速度やクラスタリングの結果がかわりますので、適宜合ったものを選択します。
以下、3つのアルゴリズムを試します。
今回試すアルゴリズムは、Non-overlapping (ノードが一つののみのコミュニティに属する場合の抽出)のタイプに属しています。
Greedyアルゴリズムで高速 : fastgreedy.community
http://www.arxiv.org/abs/cond-mat/0408187 のarxivに詳細がかかれています。
Qの増分に着目したアルゴリズムです。
# 分割をもとめる
> fc <- fastgreedy.community(g.sample)
> fc
## Graph community structure calculated with the fast greedy algorithm
## Number of communities (best split): 3
## Modularity (best split): 0.5758
## Membership vector:
## [1] 3 3 3 3 3 1 1 1 1 1 2 2 2 2 2
Number of communities (best split): 3 なので、3つのコミュニティがあることがわかります。
Modularityも0.6付近なので、比較的高い精度でクラスタリングできていることがわかります。
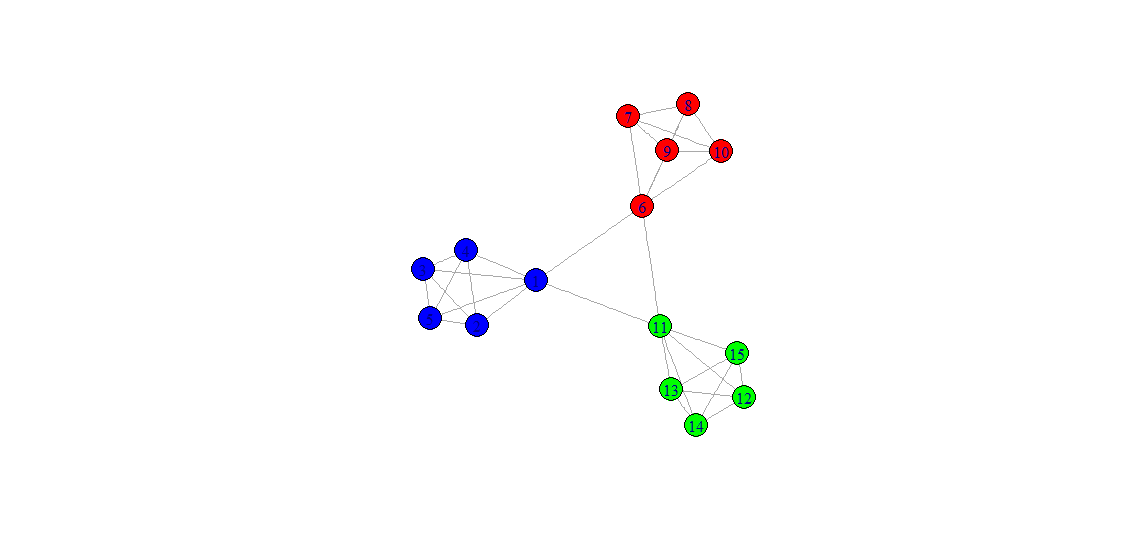
実際に色分けしてプロットしてみましょう。
# コミュニティを求めて、コミュニティ毎に色を設定
> memb <- community.to.membership(g.sample, fc$merges, steps = which.max(fc$modularity) -
1)
> V(g.sample)$color <- rainbow(length(memb$csize))[memb$membership + 1]
> plot(g.sample, layout = layout.fruchterman.reingold, edge.arrow.size = 0.5)
ランダムウォークに基づくアルゴリズム : walktrap.community
# 実行例
> wc <- walktrap.community(g.sample)
> wc
## Graph community structure calculated with the walktrap algorithm
## Number of communities (best split): 3
## Modularity (best split): 0.5758
## Membership vector:
## [1] 2 2 2 2 2 1 1 1 1 1 3 3 3 3 3
スピングラスによるアルゴリズム : spinglass.community
統計物理学のアプローチです。ちなみにスピングラス理論の第一人者は東工大の西森先生です。
# 実行例
> sc <- spinglass.community(g.sample)
> sc
## Graph community structure calculated with the spinglass algorithm
## Number of communities: 3
## Modularity: 0.5758
## Membership vector:
## [1] 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3
デンドログラムと任意ステップによる分割
クラスタリングの様子を図にする方法として、デンドログラムがあります。
# デンドログラム
> dend <- as.dendrogram(fc)
> plot(dend)
この図をみると、高さ12あたりで横に水平線をひくと、ちょうど3つのクラスタに分解されることがわかります。
試しに、Modularityが最大ではない(高さが12よりも低い)場合のクラスタリングを求めてみます。
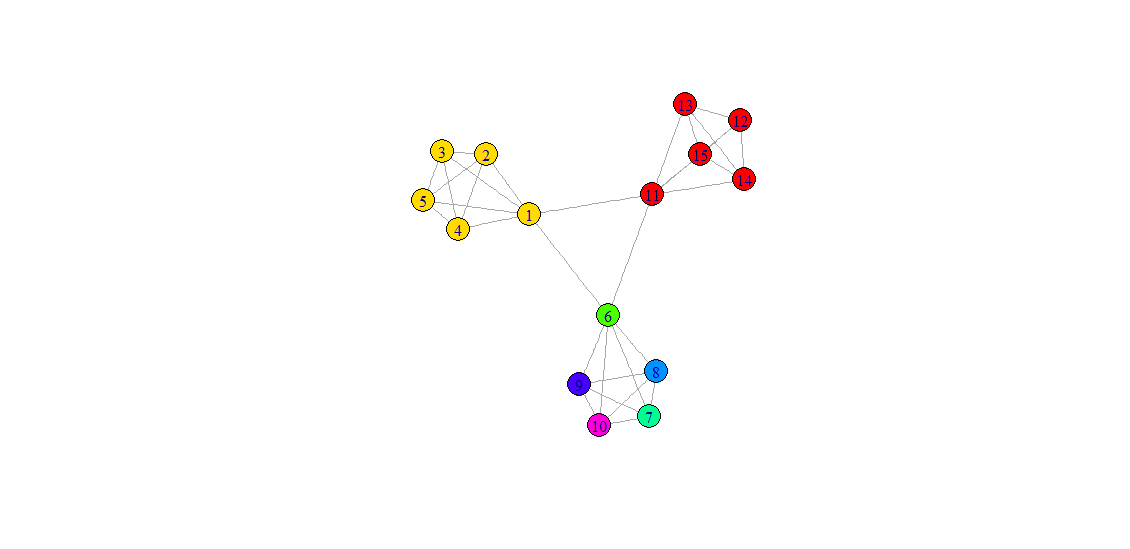
# 8stepで分割の計算を終えた場合
memb2 <- community.to.membership(g.sample, fc$merges, steps = 8) # stepに8を指定する
V(g.sample)$color <- rainbow(length(memb2$csize))[memb2$membership + 1]
plot(g.sample, layout = layout.fruchterman.reingold, edge.arrow.size = 0.5)
デンドログラムから予想されるように、3つめのクラスタが完全には分割できていませんでした。
このグラフの例はあからさまに3つのクラスタがあることが明白ですが、
実データはクラスタ具合が微妙になる(Q~0.1くらい)なので、任意のステップで計算を止めて分割することで有効な結果が得られる場合もあります。
今回は、クラスタリングアルゴリズムをいくつか試してみました。
ネットワーク解析では重要なノードを見つける「中心性解析」や、ノードが複数のコミュニティに属することを許した場合の「コミュニティ抽出」などもあります。
参考となるサイトなど
こちらのスライドがとても勉強になります。
http://www.slideshare.net/kztakemoto/r-seminar-on-igraph
stackoverflow にはRなどのやりとりがありますので、参考になると思います。
igraphのドキュメント を参考にするといいです。
他にもブログなどで実行例があると思いますので、参考になると思います。