POG上達のためのデータ解析２ 〜jupyter notebookで解析編〜

#前回までのおさらい
POG上達のためのデータ解析１　〜Pythonでwebスクレイピング〜　では2010〜2013年の期間に生まれた馬のプロフィール（性別、血統、厩舎など）とPOG期間中の獲得賞金を取得した。
得られたデータは"horse_db/horse_prof_(yyyy).csv"というファイル名で生まれ年ごとに分けて保存している。

#今回の目的
今回はこれらのデータを基に馬のプロフィールとPOG期間中の獲得賞金との間の因果関係を解析し、POG必勝の法則を見出したい。

ただし残念ながら筆者はデータ解析のスペシャリストではない。したがって、試行錯誤を重ねてなんらかの結論を導くことになるだろう。最終的には重回帰分析や機械学習のお世話になることが予想されるが、まずは簡単な解析により各因子の特徴を把握したい。

#データ解析
今回は試行錯誤を含むデータ解析に適していそうなjupyter notebook上で解析を進めることにする。また、因子ごとの統計量（平均、分散など）の算出にあたってはpandasモジュールを活用する。

##下準備
まず解析元となるデータフレームを生成する。

AnalyseUmaData_160105.ipynb

import os
import pandas as pd

year_l = range(2010, 2014)
masta_df = pd.DataFrame()
for year in year_l:
    i_dname = './horse_db/'
    i_fname = 'horse_prof_%d.csv' % year
    i_fpath = os.path.join(i_dname, i_fname)
    tmp_df = pd.read_csv(i_fpath,index_col=0, header=0, encoding='utf-8')
    masta_df = pd.concat([masta_df, tmp_df])
    
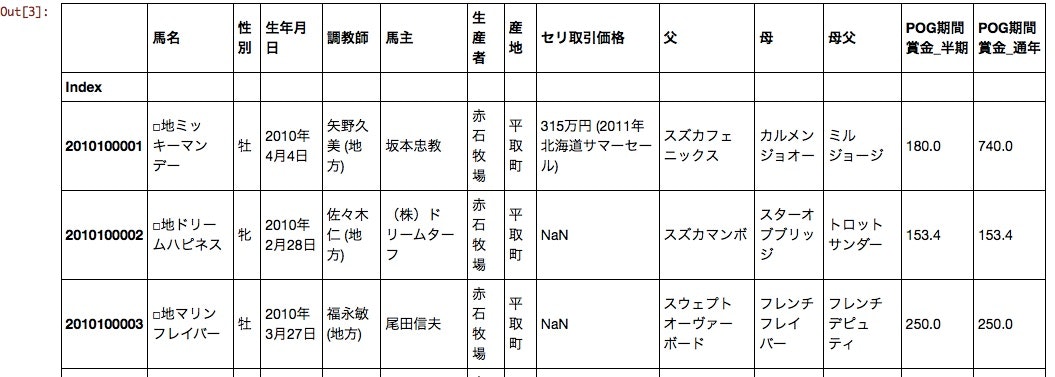
masta_df[:10]

以下に生成されたデータフレームの一部を示す。

性別、生年月日、調教師、馬主、生産者、セリ取引価格、父、母父　あたりがPOG期間賞金に影響を与えそうである。

このままでは生年月日、セリ取引価格が扱いにくいので少し成形する。

AnalyseUmaData_160105.ipynb

import datetime

#　生年月日　=>　生まれ年、生まれ月
birth_y = masta_df[u'生年月日'].dropna().map(lambda x: datetime.datetime.strptime(x.encode('utf-8'), '%Y年%m月%d日').strftime('%Y'))
birth_y.name = u'生まれ年'
birth_m = masta_df[u'生年月日'].dropna().map(lambda x: datetime.datetime.strptime(x.encode('utf-8'), '%Y年%m月%d日').strftime('%m'))
birth_m.name = u'生まれ月'
df = pd.concat([masta_df, birth_y, birth_m], axis=1)

#　セリ取引価格　文字列 => 数値化
df[u'セリ取引価格'] = masta_df[u'セリ取引価格'].fillna('-1')
df[u'セリ取引価格'] = df[u'セリ取引価格'].dropna().map(lambda x: x.replace(',', ''))
df[u'セリ取引価格'] = df[u'セリ取引価格'].dropna().map(lambda x: int(x.split(u'万円')[0]))

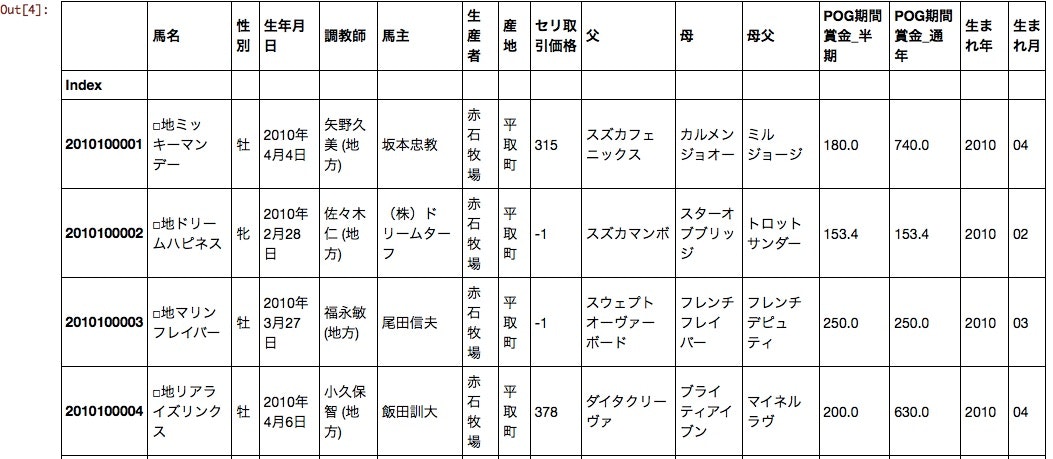
df[:10]

生年月日は生まれ年と生まれ月にわけた。これでセリ取引価格や生まれ年、生まれ月が数値データとして扱えるようになった。

##解析
それでは早速解析を始めてみよう。試行錯誤の結果、データ集計スクリプトは以下の形に落ち着いた。

AnalyseUmaData_160105.ipynb

import numpy as np

#　説明変数
param_l = [u'性別', u'生まれ月', u'調教師', u'馬主', u'生産者', u'父', u'母父']

#　目的変数
prize_l = [u'POG期間賞金_半期',u'POG期間賞金_通年']

#　設定
param = param_l[0]
prize = prize_l[1]
pts_filter = 5
prize_filter = 1000 #賞金フィルタ

#　集計
ser_ave = df.groupby(param).mean()[prize]
ser_ave.name = u'prize>=0_ave'
ser_std = df.groupby(param).std()[prize]
ser_std.name = u'prize>=0_std'
ser_pts = df.groupby(param).size()
ser_pts.name = u'prize>=0_pts'
ser_fave = df[df[prize]>=prize_filter].groupby(param).mean()[prize]
ser_fave.name = u'prize>=%d_ave' % prize_filter
ser_fstd = df[df[prize]>=prize_filter].groupby(param).std()[prize]
ser_fstd.name = u'prize>=%d_std' % prize_filter
ser_fpts = df[df[prize]>=prize_filter].groupby(param).size()
ser_fpts.name = u'prize>=%d_pts' % prize_filter
ser_fper = (df[df[prize]>=prize_filter].groupby(param).size()/df.groupby(param).size()).map(lambda x: float(x)*100)
ser_fper.name = u'prize>=%d_pts / prize>=0_pts [%%]' % prize_filter
result = pd.concat([ser_ave, ser_std, ser_pts, ser_fave, ser_fstd, ser_fpts, ser_fper],axis=1)
result.index.name = '%s_%s' % (param, prize)
result = np.round(result.sort_values(by=ser_fper.name, ascending=0),2)
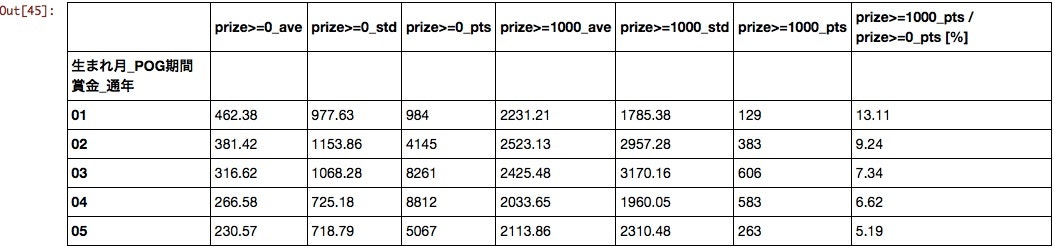
result[result[ser_fpts.name] >= pts_filter][:10]

各列には賞金が0以上、すなわちすべての馬を母集団とした場合の平均値、分散、点数と、
賞金が1000万以上の馬を母集団とした場合の平均値、分散、点数、
そして、賞金が1000万以上となる馬の割合を示している。

性別

　セン馬有利という結果となったが、POG期間中にセン馬だったかどうかは定かではない。少なくとも牝馬が不利であることがわかる。

生まれ月

　早く生まれるほど有利。

調教師

賞金フィルタの設定次第でいくらでも順位が変わる気もするが、1000万以上の割合でソートすると以下の結果となった。
2016年2月に引退が予定されているマツパク厩舎が一位となったのがなんとも残念である。

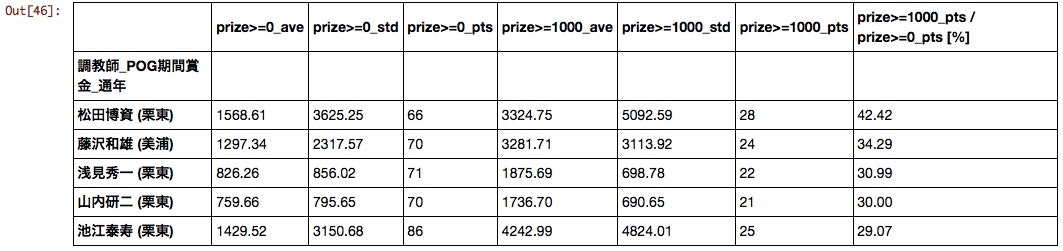
馬主

意外にもG1での活躍馬を輩出するようなクラブが上位に来ていない。クラブ馬は当たり外れの差が大きいのだろうか。

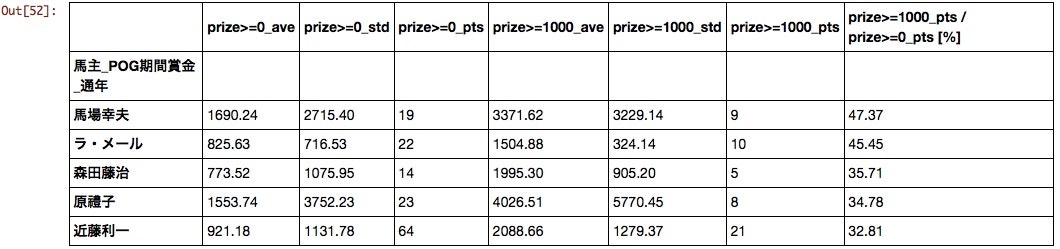
生産者

今まで「迷ったらとりあえずノーザンファーム」という考えで馬を選んでいたが、まあまあ妥当な発想であることを裏付けるデータが得られた。

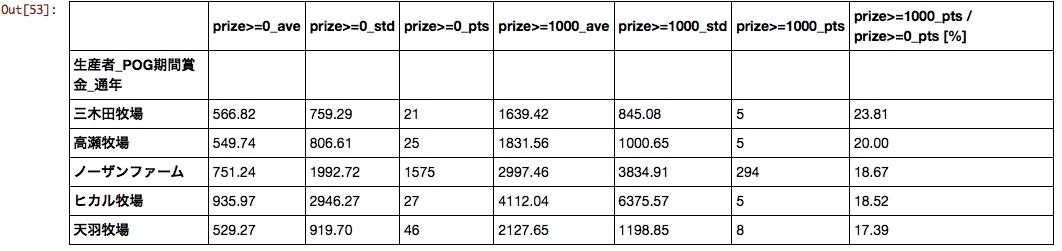
父

あまり馴染みのない海外の馬が上位にきた。母数、平均値も加味するとディープ、ダメジャー、ハーツ、キンカメあたりがPOG向けと言えるだろう。

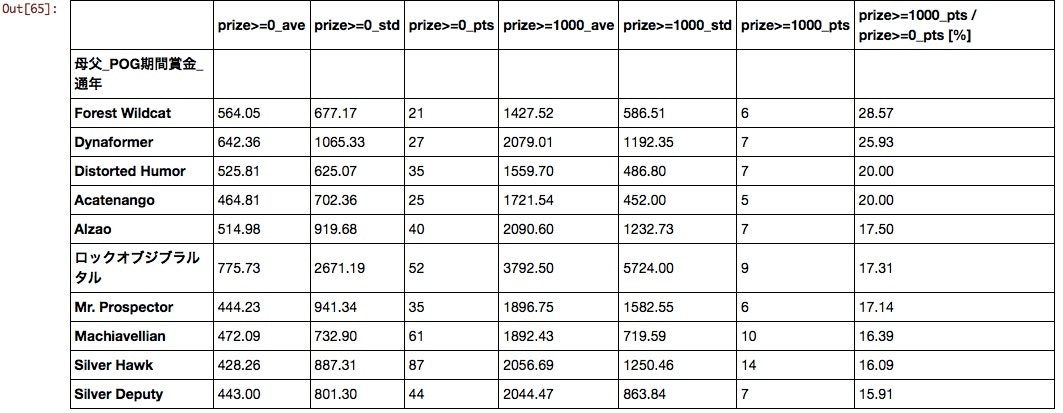
母父

もはや何が何だかわからない。近年「ステイゴールド」×「メジロマックイーン」や「ディープインパクト」×「StormCat」の組み合わせで誕生した馬の好成績が話題になったように父と母父での組み合わせで再評価する必要がありそうだ。

セリ取引価格

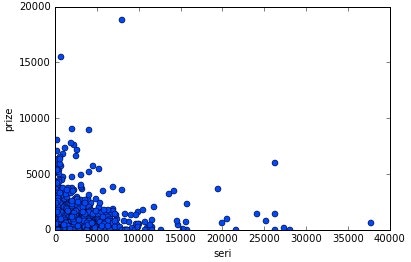
横軸：セリ取引価格、縦軸：POG期間賞金の散布図を作成した。
有意な相関が見いだせないため、POGにおいてセリ取引価格を気にする必要はなさそうである。

AnalyseUmaData_160105.ipynb

%matplotlib inline
import matplotlib.pyplot as plt

#　説明変数
param = u'セリ取引価格'

#　目的変数
prize_l = [u'POG期間賞金_半期',u'POG期間賞金_通年']
prize = prize_l[1]

#　散布図
x = df[df[param]>0][param]
y = df[df[param]>0][prize]
plt.plot(x, y, linestyle='None', marker='o')
plt.xlabel('seri')
plt.ylabel('prize')
plt.show()

今回のまとめ

今回の解析で得られた結果を総括すると、早生まれの牡馬でディープインパクト、ダイワメジャー、ハーツクライ、キングカメハメハいずれかの産駒であり個人馬主の所有馬を選択すればそこそこの確率で勝ち上がる馬を選択できそうである、ということがわかった。

しかしながら、今回の解析では賞金の閾値を1000万としたことや、各因子同士の組み合わせの効果を検証できていないなど、まだまだ改善の余地があるため、簡単に結論を出す訳にはいかない。今回の結果を踏まえ、解析手法そのものを見なおす必要もありそうである。

今後

データの可視化、重回帰分析、機械学習などに取り組む。