PyMC3で簡単なMCMCチュートリアルを試したメモ

概要

Pythonで使えるフリーなMCMCサンプラーの一つにPyMC3というものがあります．先日．「PyMC3になってPyMC2より速くなったかも…」とか「Stanは離散パラメータが…」とかいう話をスタバで隣に座った女子高生がしていた（ような気がした）ので，公式チュートリアル https://pymc-devs.github.io/pymc3/getting_started/ を試しながら，いくつかのエラーや追加実験についてのメモを書いてみました．「Pythonで階層ベイズとかを使ってみたいけどフルスクラッチでMCMC書くのはつらい…」「離散パラメータも…」みたいな人が対象です．MCMCにあまり詳しくない学生が深夜のテンションでやったので，読みにくい部分/細かいミス/理解の足りない点も多々あると思いますがご容赦ください．

※MCMCでは序盤のサンプルを捨てるのが一般的ですが，下の方の実験では，計算時間の都合でサンプルを捨てずにplotしてます．ので性能等はあくまで参考までに．

環境

自分のPC環境はOS X10.9.5, Python2.7+です．必要なものはpipで入ります．
pip install git+https://github.com/pymc-devs/pymc3
なお，PyMC3のインストールにあたっては，少し昔の記事だとURLのリンク先が異なっていることがあるので注意が必要です．PandasとPatsyもあると便利なのでpipで入れておくとよいと思います．
pip install pandas
pip install patsy

基本的な処理

エラーが起きたところを説明するためには，チュートリアルの一部を使うので，チュートリアル前半から最低限必要そうなところをまとめます．なお，今回の記事ではPyMC3依存の部分を明示的にpm.の形で書いています．チュートリアルではpm.は省かれていますが，それ以外は同じコードです．

まずいくつかimport．

import numpy as np
%pylab inline
np.random.seed(27)
import pymc3 as pm

サンプルデータセットは以下のように作っておきます．

alpha, sigma = 1, 1
beta = [1, 2.5]
size = 100
X1 = np.linspace(0, 1, size)
X2 = np.linspace(0,.2, size)
Y = alpha + beta[0]*X1 + beta[1]*X2 + np.random.randn(size)*sigma

モデル定義をします．

#X1とX2でYを線形回帰するモデル
#modelという名前のモデルを定義する，という意味
with pm.Model() as model:

    # Priors for unknown model parameters
    alpha = pm.Normal('alpha', mu=0, sd=10)
    beta = pm.Normal('beta', mu=0, sd=10, shape=2)
    sigma = pm.HalfNormal('sigma', sd=1)

    # Expected value of outcome
    mu = alpha + beta[0]*X1 + beta[1]*X2

    # Likelihood (sampling distribution) of observations
    Y_obs = pm.Normal('Y_obs', mu=mu, sd=sigma, observed=Y)

上のモデルを使ってMCMCを実行します．（手元のCPUで13.6秒かかりました）

from scipy import optimize
with model:
    # obtain starting values via MAP
    start = pm.find_MAP(fmin=optimize.fmin_powell)
    # instantiate sampler
    step = pm.Slice(vars=[sigma])
    # draw 5000 posterior samples
    trace = pm.sample(5000, start=start, step=step)

pm.sample( )の引数ですが，最初の5000は得たいsampleのサイズです．次のstartでは初期値を設定しています．今回はMAP推定量を使っていますが，指定しないことも可能です．最後のstepではスライスサンプリングを指定していますが，指定しない場合は，
・2値変数：BinaryMetropolis
・離散変数：Metropolis
・連続変数：NUTS
がデフォルトで割り当てられます．ここで使用した簡単なモデルでは，サンプリング方法による差はほぼ見られませんでした．なお，Stanで使用できるHamiltonianMCとNUTSはPyMC3でも使用できます．

可視化は非常に簡単で，以下のようにtraceplotで一発です．

pm.traceplot(trace[4000:])

要約情報も以下のように見ることができます．

pm.summary(trace[4000:])

なお，今回は簡単のため正規分布のみを扱いましたが，もちろん他にもガンマ分布，ベータ分布，二項分布，ポアソン分布などなど色々な分布が扱えます．

※PyMC2との関係などについては，http://breakbee.hatenablog.jp/entry/2014/08/04/031342 などが参考になりました．

困った点

そんな便利なPyMC3ですが，いくつか困る点があります．チュートリアルを試しながら見ていきます．

1. theanoのメソッドとかを使うとエラーを吐く

ちょうど先日Twitterでこれ関連の議論を見た気がしますが，おそらくこの場合エラーの元凶は https://github.com/pymc-devs/pymc3/blob/master/pymc3/model.py の最後の行

theano.config.compute_test_value = 'raise'

にあります（参考：https://sites.google.com/site/iwanamidatascience/vol1/support_tokushu ）．自分にはキャッシュがどうといった細かいことはわからないのですが，PyMC3をimportした後で

import theano
theano.config.compute_test_value = 'ignore'

と無心で打ち込めば解消できました．ちなみに，'ignore'ではなくて'off'と書くこともできるそうですが，glmの計算などで
scratchpad instance has no attribute 'test_value'
というエラーが出たりするので，とりあえず'ignore'にするのが無難かなと思います．ちなみに，公式ExamplesのProbabilistic Matrix Factorizationのページでも'ignore'になっています．

2. 自作の関数やクラスの扱いが厄介

2.1 as_op不要説

チュートリアルのArbitrary deterministicsセクションでは，deterministicな変数bを以下のcrazy_modulo3( )関数で求めています．

import theano.tensor as T 
from theano.compile.ops import as_op

@as_op(itypes=[T.lscalar], otypes=[T.lscalar])
def crazy_modulo3(value):
    if value > 0: 
        return value % 3
    else :
        return (-value + 1) % 3

with pm.Model() as model_deterministic:
    a = pm.Poisson('a', 1)
    b = crazy_modulo3(a)

@as_op( )の部分はtheano.tensor型の変数を計算する関数を使うための呪文みたいなもので，関数を定義する直前の行に書き，入出力の型を宣言してあげます．PyMC3のチュートリアルにもこのように書かれています．

Theano needs to know the types of the inputs and outputs of a function, which are specified for as_op by itypes for inputs and otypes for outputs.

しかし，実はここは@as_opを使わなくても以下のように定義できます．

import theano.ifelse
def symbolf(x):
    return theano.ifelse.ifelse(T.gt(x,0), x%3, (-x+1)%3)
def crazy_modulo3(value):
    return symbolf(value)

ここは少しハマったので解説します．

例えば，ifelseを使わずナイーブに

def crazy_modulo3(value):
    if value > 0:
        return value % 3
    else :
        return (-value + 1) % 3

とすると，value > 0という比較が出来ないと怒られます．また，

def crazy_modulo3(value):
    if T.lt(0,value):
        return value % 3
    else :
        return (-value + 1) % 3

とすると，エラーは出ないのですが，値をtraceしてみるとT.lt(0,value)がFalseにならない（Theano has no boolean dtype. Instead, all boolean tensors are represented in 'int8'. -- http://deeplearning.net/software/theano/library/tensor/basic.html ）ことがわかります．
そのため，ifelseを使って無理矢理比較しています．この辺がちょっとtheanoのつらいところですが，これで一応@as_opを使わずに関数を定義できました．

2.2 deterministicな変数をtraceplotする方法

上のコードでdeterministicな変数bを定義したはいいものの，チュートリアルにはその後のサンプリング方法については書いていません．そこで試しに

with model_deterministic:
    trace = pm.sample(500)
pm.traceplot(trace)

としてみると，変数aの値しかplotされません．自分は変数bにも興味があったので，pm.の中身を眺めてみると，pm.Deterministic( )というそれっぽいものを発見しました．あとはモデルの定義で
b = crazy_modulo3(a)
を
b = pm.Deterministic("b",crazy_modulo3(a))
に変えてサンプリングすると，bの値が正しくplotされるはずです．

2.3 as_opをランダム変数の計算に使うのは避けるべき

チュートリアルのArbitrary distributionsセクションでは，自分でサンプリングしたい確率分布を定義する方法を以下のように書いています．

with pm.Model() as model1:
    alpha = pm.Uniform('intercept', -100, 100)
    # Create custom densities
    beta = pm.DensityDist('beta', lambda value: -1.5 * T.log(1 + value**2), testval=0)
    eps = pm.DensityDist('eps', lambda value: -T.log(T.abs_(value)), testval=1)
    # Create likelihood
    like = pm.Normal('y_est', mu=alpha + beta * X, sd=eps, observed=Y)

lambda式とpm.DensityDistによって定義するこの方式は特に問題ありません．続けて以下のようにサンプリングしても正しく動きます．

with model1:
    trace = pm.sample(500)
pm.traceplot(trace)

これと同様の意味を持つコードとして，チュートリアルでは，クラスを定義する以下の方式を採用しています（すぐ後でこのコードに誤りがありそうなことを指摘します）．これだと，lambda式を使わないので，関数が書きやすくなるメリットがあるように思われます．なお，beta以外は上のmodel1と同じ形になるよう私が付け加えたパラメータです．

class Beta(pm.distributions.Continuous):
    def __init__(self, mu, *args, **kwargs):
        super(Beta, self).__init__(*args, **kwargs)
        self.mu = mu
        self.mode = mu

    def logp(self, value):
        mu = self.mu
        return beta_logp(value - mu)

@as_op(itypes=[T.dscalar], otypes=[T.dscalar])
def beta_logp(value):
    return -1.5 * np.log(1 + (value)**2)

with pm.Model() as model2:
    beta = Beta('slope', mu=0, testval=0)

    #I add other parameters to follow model1 above
    alpha = pm.Uniform('intercept', -100, 100)
    eps = pm.DensityDist('eps', lambda value: -T.log(T.abs_(value)), testval=1)
    like = pm.Normal('y_est', mu=alpha + beta * X, sd=eps, observed=Y)

betaの計算に例の@as_opが出てきました．先ほどのdeterministicな変数の計算にこれを使ったときは，サンプリングしても問題なく動きましたが，今回はどうでしょうか？

with model2:
    trace = pm.sample(100)
pm.traceplot(trace)

これを実行すると，おそらく↓のエラーが出たと思います．
AttributeError: 'FromFunctionOp' object has no attribute 'grad'

どうも，@as_opによって持ってきたオブジェクトは，MCMCサンプリングで必要な勾配計算の属性gradを持っていない，というメッセージに思えます．deterministicな変数では勾配計算しないのでオッケーだったんでしょうか．この辺をおもむろにググってみると，偉い人による「対処法はわからない」といった回答が見つかりました．

The only way to get the automatic gradient computation is by expressing your density in terms of theano operators. as_op creates a blackbox function for which autodiff will not work so there is no way I know of (except numerical differentiation) to make this work.
https://github.com/pymc-devs/pymc3/issues/601

しかし，ここで2.1の結果がいきます．つまり，@as_opが悪さをしているならそもそも@as_opなしで定義すればいいのでは？という話です．そこで，

@as_op(itypes=[T.dscalar], otypes=[T.dscalar])
def beta_logp(value):
    return -1.5 * np.log(1 + (value)**2)

を以下のように書き変えます．

def beta_logp(value):
    return -1.5 * T.log(1 + (value)**2)

2.1と同じように，theano.tensor型の変数を扱う際のルールに注意すれば（今回だと，np.logではなくT.logにする）無事計算できます．結果も概ね同じになりました（サンプリングなのでブレはありますが）．

結論としては，自作の関数やクラスを使うときは，lambda式を使おうが使わまいが，theanoの文法に注意してコーディングする必要がある，ということが言えそうです．

3. glmでの速度と性能

最後に，一般化線形モデル(glm)の計算を行うときの速度と性能の話をします． 詳細は https://github.com/pymc-devs/pymc3/issues/544 にありますが，「デフォルトだとしばしばNUTSが遅い」「Metropolisは速い」「データやマシンのタイプによっては，HamiltonianMCが速いときもある」といった話がされています．参考までに，自分の環境でチュートリアルのデータをglm（普通の線形回帰）にかけてみました．

import pandas as pd
df = pd.DataFrame({'x1': X1, 'x2': X2, 'y': Y})
with pm.Model() as model:
    pm.glm.glm('y ~ x1+x2', df)
    start = pm.find_MAP(fmin=optimize.fmin_powell)
    step = pm.HamiltonianMC()
    trace = pm.sample(1000, start=start, step=step)
pm.traceplot(trace)

・HamiltonianMC：1.7秒で終了．収束もまあまあ．（図1）
・Metropolis：0.3秒で終了．収束はダメダメ．
・NUTS：5分経っても8個しかサンプルできてない，遅すぎる
・本記事1.で行った，pm.glmクラスを使わない手書きのサンプリング：3.2秒で終了．HamiltonianMCには収束は劣るが，それほど悪くない．（図2）

真のパラメータ：alpha=1,beta[0]=1,beta[1]=2.5,sigma=1
（図1）

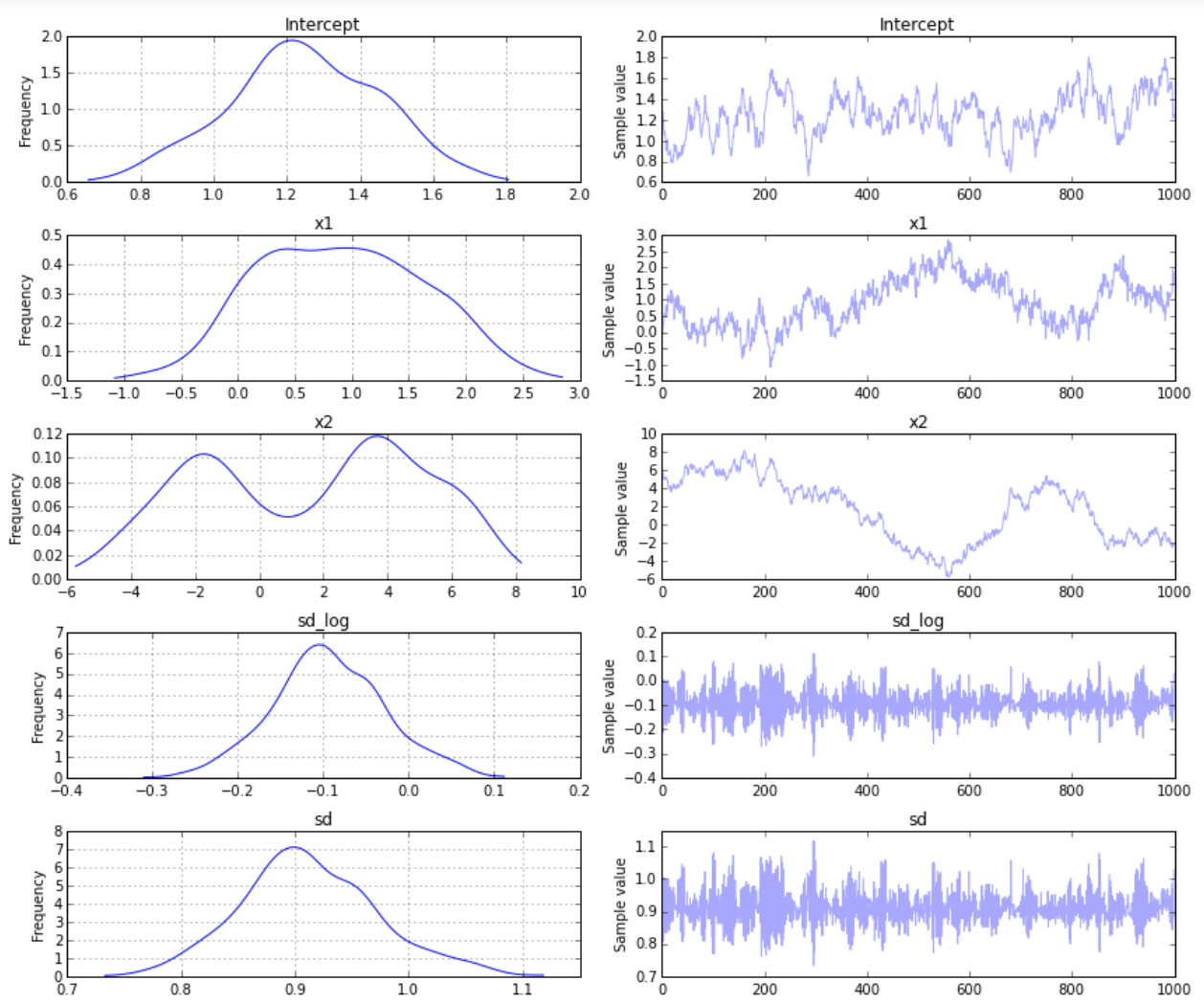
（図2：betaの青線がX1の回帰係数，緑線がX2の回帰係数，sigmaがsdにそれぞれ対応）

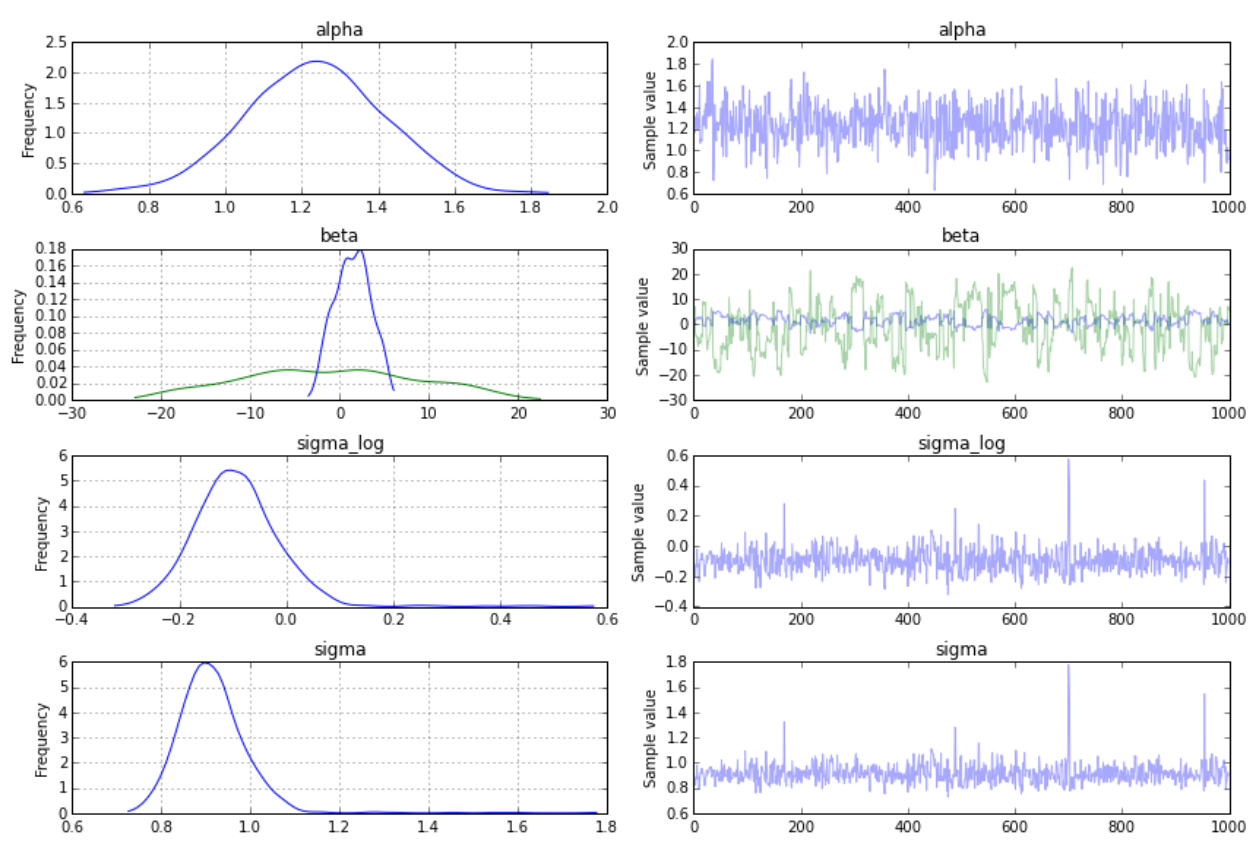
という結果でした．ちなみに，NUTSを途中で打ち切ってplotしてみると，どうもパラメータのscalingがおかしいように見えます．この場合の解決法として，上のissueページには

C = pm.approx_hessian(model.test_point)
step = pm.NUTS(scaling=C)

とすれば速度が出ると書かれています．Sphinxのバージョンをupdateして（入ってない人はpipでinstallして下さい）上の2行を無心で打ち込んだところ，leading minorが正定値じゃないので計算できませんと言われました．
LinAlgError: 2-th leading minor not positive definite

これはちょっと解決できそうにないのでスルーしましたが，関連する議論はこちらにありそうです→ https://github.com/scikit-learn/scikit-learn/issues/2640

個人的な感想としては，単にglmを使いたいなら，approx_hessianをscalingに使ったNUTSによるglmを試してみて，ダメだったらHMCによるglmを試してみるのがよさそうです．

また，1.の例で書いたようなpm.glmクラスを使わない方法も，priorをうまく設定するなど工夫すれば性能が上がる可能性がありそうですし，ハイパーパラメータの挙動を見たい場合やもっと複雑な階層ベイズモデルを使いたいときなどは，pm.glmを使わずにこちらを採用すればよいかなと思いました．

最後に

自分のメモがてらダラダラ長く書きましたが，ハマりそうなところの参考に少しでもなれば幸いです．@as_opのところは，自分でtheano側のgradを定義し直そうとして一晩を無駄にするなどなかなかつらいものがありました．

あと，公式ページはチュートリアルよりExamplesの方が面白そうな（Probabilistic Matrix FactorizationとかSurvival Analysisとか）予感がするので，また深夜の気が向いたときに試してみようと思います．

※ gradの定義はhttp://deeplearning.net/software/theano/extending/op.html を参考にしました．元々定義されているT.gradをtheano.functionで作れる関数とみたときの入力はリストのように思えるのですが，このチュートリアル通りにやると，入力がリストとなる関数が定義できずに断念しました．

適宜追記します．