Remez algorithmについて

最小二乗近似とミニマックス近似

最小二乗近似は二乗誤差の総和が最小になるような係数を求めるのに対してミニマックス近似は絶対値最大の誤差が最小になるように係数を求めます。最小二乗近似より面倒くさいです。某音ゲーで例えるとライブ成功とフルコンボの違いのようなものです。

最小二乗フィルタ

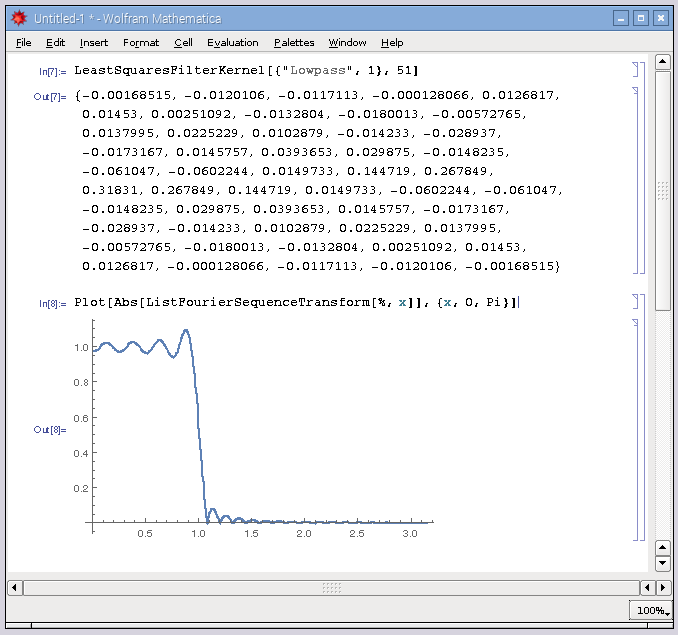
遮断周波数が1.0の51次の最小二乗ローパスフィルタです。Raspberry PiのMathematicaでお手軽に計算することが出来ます。

等リプルフィルタ

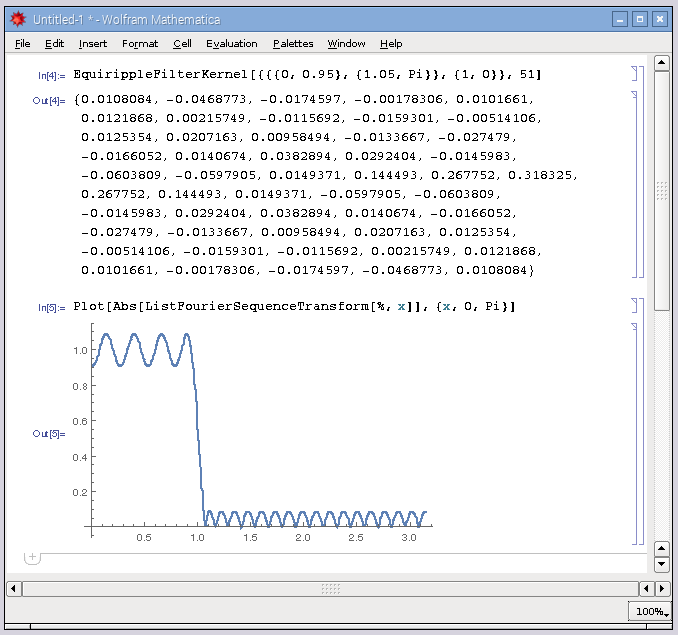
遮断周波数が1.0の51次の等リプルローパスフィルタです。今回はこれを自前で計算するのが目標です。

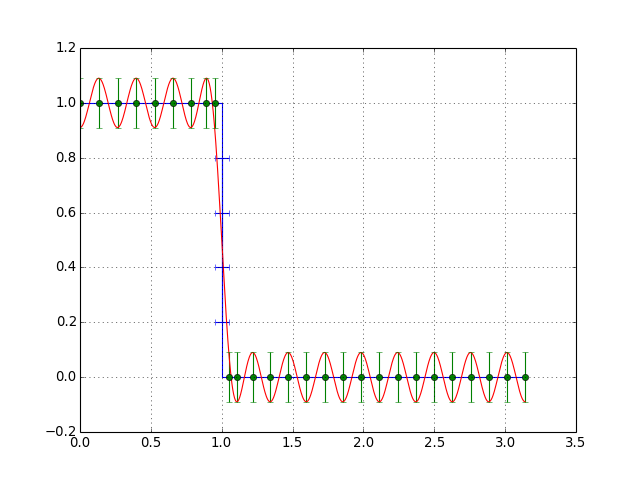
ミニマックス近似

最良近似多項式

$f(x)$は区間$[a,b]$で連続な関数でそれを近似する$n$次多項式を

f_n(x)=\sum_{k=0}^n a_k x^k

とします。$n$を固定したときに

 \max_{a<x<b} |f(x)-f_n(x)|

を最小にするような多項式を最良近似多項式といいます。最良近似多項式は次のような性質を持っています。

$f_n(x)$が最良近似多項式であるための必要十分条件は、誤差関数$\epsilon(x)$を

\epsilon(x) = f(x)-f_n(x)

と置いたとき、$|\epsilon(x)|$が区間$[a,b]$で少なくとも$n+2$点で等しい最大値をとり、最大値における$\epsilon(x)$の符号が交互に並んでいることである。

あと最良近似多項式の一意性についてもいわないとですが割愛します。

最良近似三角多項式

$g(x)$は区間$[0,\pi]$で連続な関数でそれを近似する三角多項式を

g_n(x)= \sum_{k=0}^n a_k \cos(kx)

とします。今回は偶関数を扱うので$\sin$関数は無しとさせてください。実は多項式の場合と同じような性質を持っています。

$g_n$が区間$[0,\pi]$で連続な関数$g$の最良近似とのなる必要十分条件は、誤差関数$\epsilon(x)$を

\epsilon(x) = g(x)-g_n(x)

と置いたとき、$|\epsilon(x)|$が区間$[0,\pi]$で少なくとも$n+2$点で等しい最大値をとり、最大値における$\epsilon(x)$の符号が交互に並んでいることである。

Remez algorithm

今回はRemez algorithmを用いて等リプルフィルタを作成します。アルゴリズムは次のようになっています。

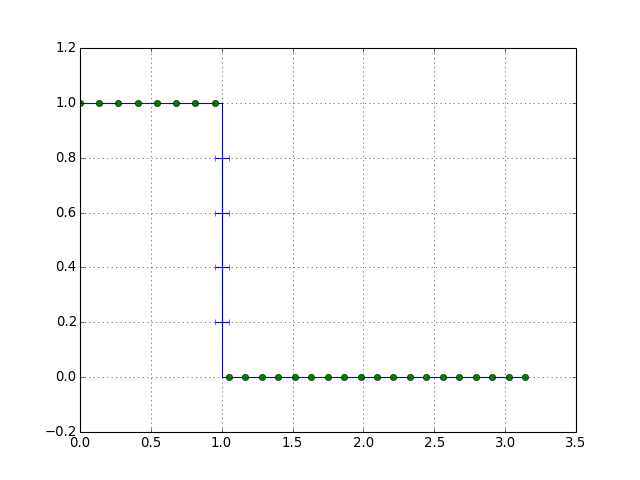
1. 区間$[0, \pi]$上に$n+2$個の検査点$x_0, \cdots x_{n+1}$を適当に用意する
2. 検査点での誤差関数$\epsilon(x)$の絶対値が等しくかつ誤差の符号が交互に並ぶような三角多項式$g(x)$の係数$a_0, \cdots, a_n$と誤差$d$を求め、三角多項式を更新する
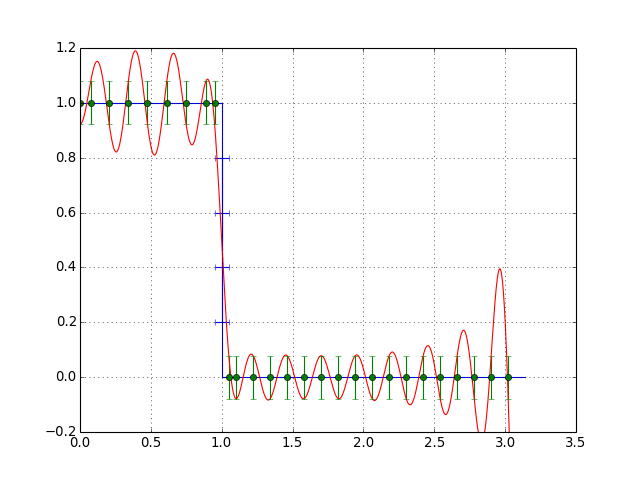
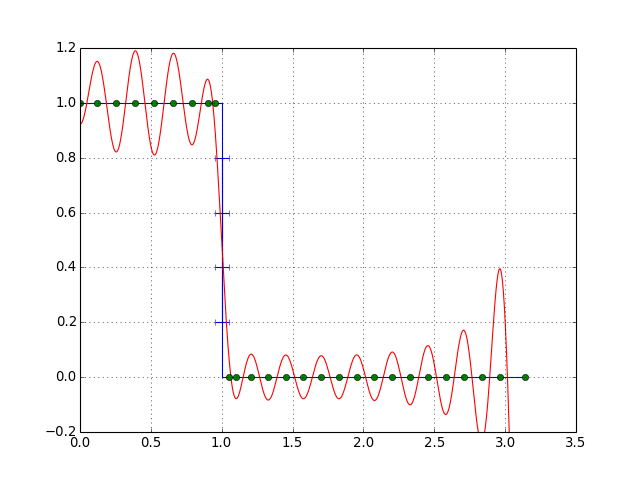
3. 誤差関数$\epsilon(x)$の絶対値が最大となる$n+2$個の点$x_0, \cdots x_{n+1}$を求め、検査点を更新する
4. 検査点での誤差関数$\epsilon(x)$の絶対値が等しくかつ誤差の符号が交互に並んでいれば終了し、そうでなければ2へ戻る

4はそのまんま、2は連立一次方程式を解けば良さそう（解き方はいろいろありますが）、しかし1と3は試行錯誤が必要そうですね。

実装

Pythonで200行程度で実装しました。入力値によってはコケるので万能ではないです。

• https://github.com/fukuroder/Remez_algorithm_test

Remez algorithm（本体）

アルゴリズムそのまんまです。

FIR-LPF-Remez-algorithm.py(抜粋)

######################
# Remez algorithm 本体
######################
def remez(
    order,         # フィルタの次数
    w0,            # 遮断周波数
    h,             # 遷移幅
    max_iter=100): # 最大反復回数

    n = (order-1)//2 # 三角多項式の次数

    # Remez algorithm --step1--
    # 検査点の初期値を生成
    list_x = initialize_extreme_points(n, w0, h)

    for count in range(1, max_iter+1):
        # Remez algorithm --step2--
        # 検査点(x[0],...,x[n+1])での誤差の符号が交互に反転するような
        # 三角多項式係数(a[0],...a[n])と誤差dを求める
        list_a, d = update_tri_polynomial_coefficients(list_x, w0)

        # Remez algorithm --step3--
        # 誤差関数の絶対値が最大となるn+2個の点を求める
        list_x = update_maximum_error_points(list_a, w0, h)

        # Remez algorithm --step4--
        # 収束判定（誤差の絶対値が等しくかつ符号が交互に並んでいれば終了）
        if check_convergence(list_a, list_x, w0):
            # cos関数系からexp関数系の表現に変換
            list_h = [a*0.5 for a in reversed(list_a[1:])] + \
                     [list_a[0]] + \
                     [a*0.5 for a in list_a[1:]]
            return list_h, d, list_x, count
    else:
        raise Exception("[ERROR]Remez algorithm failed")

Remez algorithm step1（初期点の生成）

適当に等間隔でn+2個の点を生成します。その際に遷移域に点が入らないようにしました。

FIR-LPF-Remez-algorithm.py(抜粋)

###########################
# Remez algorithm --step1--
# 検査点の初期値を生成
###########################
def initialize_extreme_points(
    n,  # 三角多項式の次数
    w0, # 遮断周波数
    h): # 遷移幅

    # 通過域点数＋阻止域点数
    num_point = n+2;

    # 通過域点数
    num_passband_point = int(num_point*w0/math.pi)

    # 阻止域点数
    num_stopband_point = num_point-num_passband_point

    # 初期点を生成
    return numpy.append(
        numpy.linspace(     0.0, w0-0.5*h, num_passband_point),
        numpy.linspace(w0+0.5*h,  math.pi, num_stopband_point))

Remez algorithm step2（三角多項式の更新）

連立一次方程式の組み立てと三角多項式の更新を行います。ここで登場する連立一次方程式は小規模な密行列なので素直に直接法を使用しました。

FIR-LPF-Remez-algorithm.py(抜粋)

##########################################################
# Remez algorithm --step2--
# 検査点(x[0],...,x[n+1])での誤差の符号が交互に反転するような
# 三角多項式係数(a[0],...a[n])と誤差dを求める
##########################################################
def update_tri_polynomial_coefficients(
    list_x, # 検査点
    w0):    # 遮断周波数

    # 行列A作成
    matrix_A = numpy.array(
        [[math.cos(x*k) for k in range(len(list_x)-1)] + [(-1)**j] \
                        for j,x in enumerate(list_x)])

    # ベクトルb作成
    vector_b = numpy.array([ideal_lowpass_filter(x, w0) for x in list_x])

    # 連立方程式を解く
    u = numpy.linalg.solve(matrix_A, vector_b)

    # a[0],...,a[n], d
    return u[:-1], u[-1]

Remez algorithm step3（検査点の更新）

誤差関数の絶対値が最大となるn+2個の点を新しい検査点とします。三角多項式の極値は誤差の絶対値が最大になりそうです。しかし三角多項式の極値点のみでは目標のn+2個に到達しません。そのため遷移域の開始終了位置も検査点に追加します。最後に検査点は丁度n+2個でないとstep2でコケますので破綻しないように適当に調整します。それでも入力値によってはコケることがあるのでもう少しがんばらないといけないのですが泥臭くなるので諦めました。

FIR-LPF-Remez-algorithm.py(抜粋)

###########################################
# Remez algorithm --step3--
# 誤差関数の絶対値が最大となるn+2個の点を求める
###########################################
def update_maximum_error_points(
    list_a, # 三角多項式の係数列
    w0,     # 遮断周波数
    h):     # 遷移幅

    # 三角多項式の次数
    n = len(list_a)-1

    # 三角多項式の極値点を求める
    extreme_points = search_extreme_points(list_a, (n+2)*10)

    # 遷移域の開始終了位置も極値点だと思う
    extreme_points.append(w0-h*0.5)
    extreme_points.append(w0+h*0.5)
    extreme_points.sort()

    if len(extreme_points) == n+1:
        # 極値点数がn+1ならば端点(x=pi)も極値点だと思う
        extreme_points.append(math.pi)
        return extreme_points

    elif len(extreme_points) == n+2:
        # そのままでOK
        return extreme_points

    elif len(extreme_points) == n+3:
        # 極値点数がn+3ならば端点(x=0)を極値点から外す
        extreme_points.pop(0)
        return extreme_points

    else:
        raise Exception("[ERROR]number of extreme point " + \
            str(n+2) + "->" + str(len(extreme_points)))

三角多項式の極値点を全て求める方法ですが、適当に点列を発生させて三角多項式の一次導関数の符号が変わる区間を探して極値点のあたりを付けます。そのあとにニュートン法で解を求めます。エレガントな方法ではありませんが・・・。

FIR-LPF-Remez-algorithm.py(抜粋)

# 極値点を全て求める
def search_extreme_points(
    list_a,      # 三角多項式の係数列
    div):        # 分割数

    # f(x)
    def f(x):
        return d_tri_polynomial(x, list_a);

    # f(x)の導関数
    def df(x):
        return dd_tri_polynomial(x, list_a);

    # ニュートン法
    def newton(x0):
        x = x0
        for _ in range(100):
            x_next = x - f(x)/df(x)
            if abs(x_next - x) < 1.0e-8:
                break
            x = x_next
        else:
            print("[WARNING]Newton method iterations reached the limit(x=" + str(x0) + ")")
        return x

    # 点列を生成
    check_points = numpy.linspace(0.0, math.pi, div)

    # f(x)の符号が変わる区間を探す
    sign_reverse_section = \
        [p for p in zip(check_points, check_points[1:]) if f(p[0])*f(p[1]) <= 0.0]

    # f(x)=0になるxを全て求める
    return [newton(x) for x,_ in sign_reverse_section]

Remez algorithm step4（収束判定）

やり方は何でもいいですが、分散がほとんど0だった場合にOKとしました。

FIR-LPF-Remez-algorithm.py(抜粋)

#############################################################
# Remez algorithm --step4--
# 収束判定（誤差の絶対値が等しくかつ符号が交互に並んでいれば終了）
#############################################################
def check_convergence(
    list_a, # 三角多項式の係数列
    list_x, # 検査点列
    w0):    # 遮断周波数

    # 誤差関数
    def ef(x):
        return tri_polynomial(x, list_a)-ideal_lowpass_filter(x, w0)

    return numpy.var([ef(x)*(-1)**k for k,x in enumerate(list_x)]) < 1.0e-12

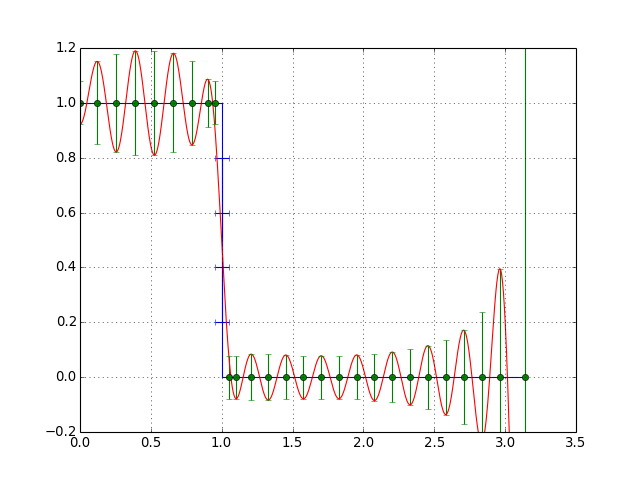
実行結果

フィルタ次数:51、遮断周波数:1.0、遷移幅0.1で実行。

フィルタ係数

0.0107713139262
-0.0468904946135
-0.01738547837
-0.00180941392864
0.0101732465807
0.0121972695875
0.00214384802868
-0.0115676650969
-0.0159117634133
-0.00513805260228
0.0125239879163
0.0207019219532
0.00957031009648
-0.0133710951659
-0.027463740521
-0.0165888267131
0.0140691206175
0.0382895442729
0.0292522135743
-0.0145891015438
-0.0603882456453
-0.0598120634071
0.0149097733243
0.144466447581
0.267735413885
0.318315208685
0.267735413885
0.144466447581
0.0149097733243
-0.0598120634071
-0.0603882456453
-0.0145891015438
0.0292522135743
0.0382895442729
0.0140691206175
-0.0165888267131
-0.027463740521
-0.0133710951659
0.00957031009648
0.0207019219532
0.0125239879163
-0.00513805260228
-0.0159117634133
-0.0115676650969
0.00214384802868
0.0121972695875
0.0101732465807
-0.00180941392864
-0.01738547837
-0.0468904946135
0.0107713139262

Mathematicaの結果と比較するとフィルタの係数が微妙に合ってないような気もしますが。

参考文献

• 加藤敏夫、復刊 位相解析(共立出版)
• 谷萩隆嗣、ディジタルフィルタと信号処理(コロナ社)