ゼロから作るDeep Learning――Pythonで学ぶディープラーニングの理論と実装を読みましたので、機械学習についてざっくりとまとめます。
できるだけ数式とかは使わない感じで説明していきますので、イメージだけつかんでもらえればと思います。
機械学習とは
機械学習は入力データから反復的に学習を行うことによって、パターンを学習し、新しいデータに対しても答えを得ることができるようにするものです。
機械学習の問題はデータから数値を予測する「回帰問題」とデータがどのクラスに属するか分類する「分類問題」の2つに大別できます。
ある問題に対する適切なパラメータを学習していくため、学習するためのデータさえ用意できれば基本的なアルゴリズムを変更することなく様々な問題を解決していくことができます。
機械学習の手順
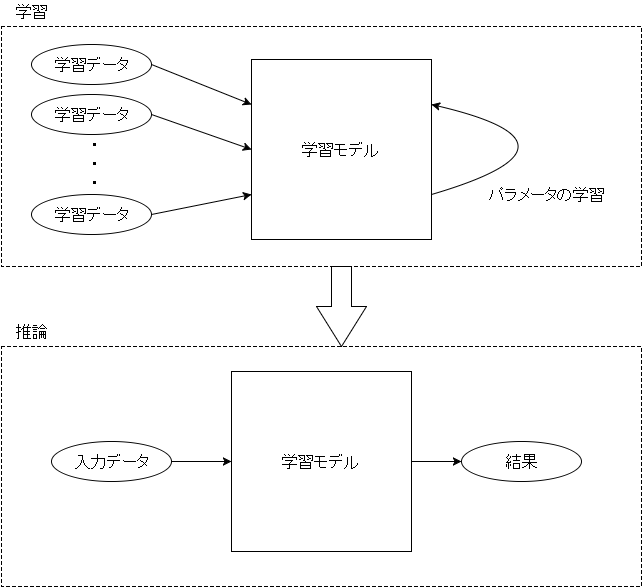
機械学習では、まず学習モデルの構築を行います。
学習モデルは多くの数式を含むモデルです。
数式にはパラメータが含まれており、それらのパラメータを決定する「学習」を行った後、学習後のモデルを使って新しい問題を解く「推論」を行います。
パラメータの学習
機械学習の「学習」とは学習モデル内のパラメータを入力データから決定していくことを指します。
問題に対してすべてのパラメータを適切に設定することは人間にはほぼ不可能であるため、(一部のハイパーパラメータ以外を)コンピュータに学習してもらいます。
損失関数と勾配法
損失関数は学習モデルの性能の悪さを評価するための関数です。
損失関数の結果が0に近いほど学習モデルは適切な学習ができているということになります。
そのため、学習では損失関数の結果が小さくなるようにパラメータを変化させていきます。
パラメータを変化させるためには勾配法という方法を使います。
勾配法は損失関数の勾配(微分)が小さくなるようにパラメータを徐々に更新していきます。
微分は関数の変化率なので、微分が0の場所は関数の最小値である可能性があるからです。
この時、微分値に対してどの程度パラメータを更新するかという学習率というハイパーパラメータを与えます。
学習率は大きくても小さくても適切な学習が実行されません。
微分はパラメータを微小変化させた時の関数の変化量です。
求めるための方法としては、実際にパラメータを微小変化させて結果の差分を計算する数値微分があります。
しかし、より効率的で高速な方法として誤差逆伝播法(バックプロパゲーション)という方法を使うのが一般的です。
誤差逆伝播法
微分はパラメータを変化させた時、最終結果がどの程度変化するかという影響度だと考えることができます。
しかし、機械学習のモデルでは数式同士が複雑に影響しあうため、微分を求めることが困難です。
そこで数式を分解し、その最小単位ごとに入力が出力にどれくらい影響を及ぼすかを計算可能な局所的な微分式を求めておきます。
それを、出力側から逆に辿っていくことで全体の微分を求めることができます。
出力から入力まで逆方向に計算をたどっていくので逆伝播という名前になっているわけです。
図の黒字が順方向の計算であり、赤字が逆方向の計算(各項の影響度)です。
例えば、100の項が1増えて101になった場合、最終結果は604になるため、100の項の影響度は4になります。
学習モデル
機械学習の学習モデルは様々なものがありますが、ディープラーニング関連の学習モデルを説明していきます。
後に行くほど複雑なアルゴリズムになりますが、その分精度が上がります。
パーセプトロン
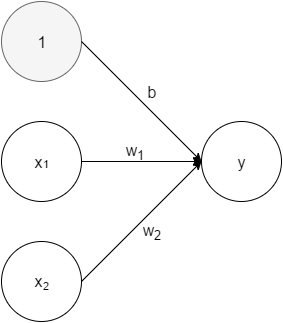
パーセプトロンは入力とパラメータの積和が閾値以下であれば0、閾値より上であれば1を出力する単純なモデルです。
多くの場合、閾値$\theta$をバイアス$-b$と置き換え、計算結果が0以下か、0より上かで出力を変化させます。
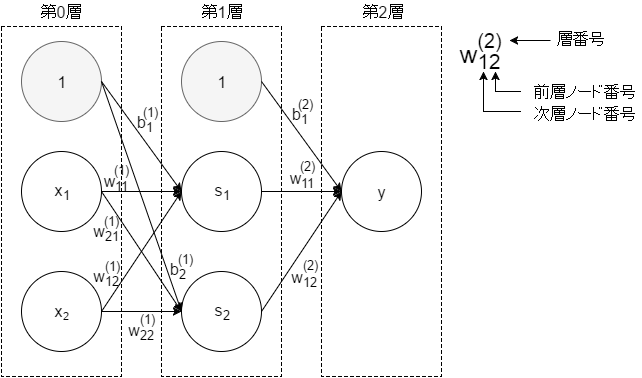
パーセプトロンが一つだけでは単純なモデルしか表現できないため、複雑なモデルを表現するためにはパーセプトロンを複数層重ねます。
ニューラルネットワーク
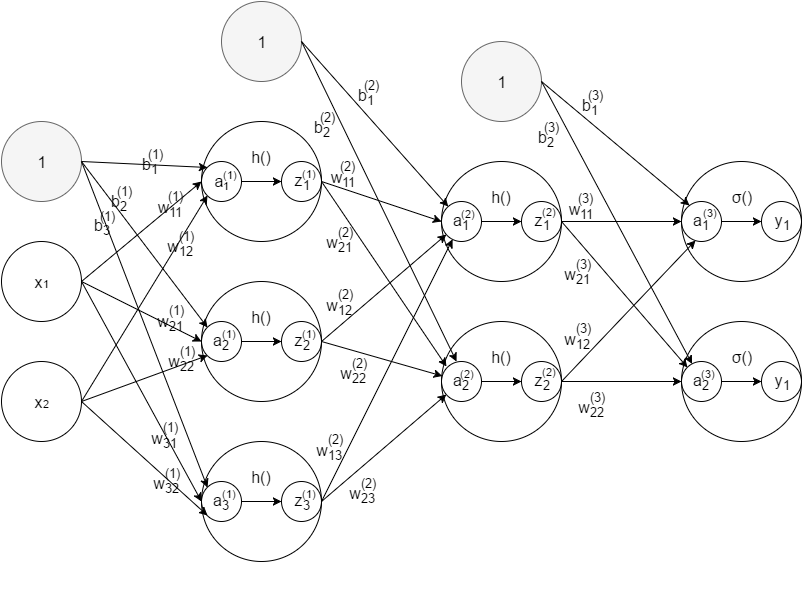
ニューラルネットワークは、構造自体はパーセプトロンに非常に似ています。
ニューラルネットワークとパーセプトロンの一番の違いは活性化関数です。
活性化関数$h$は入力信号とパラメータの積和の結果$a$を次の入力$z$に変換する関数のことです。
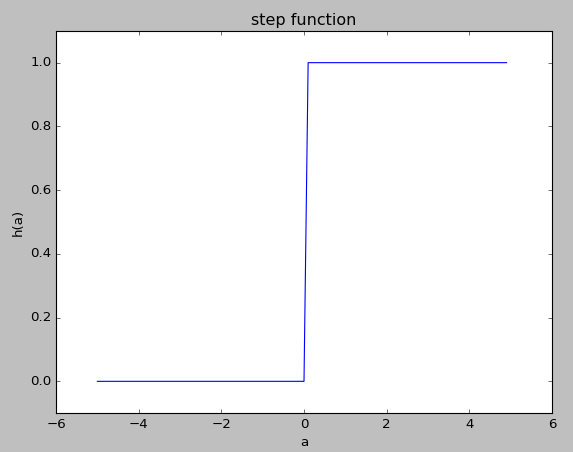
パーセプトロンでは、積和の結果が0以上の場合に1、それ以外の場合に0だったので活性化関数にステップ関数を用いていたことになります。
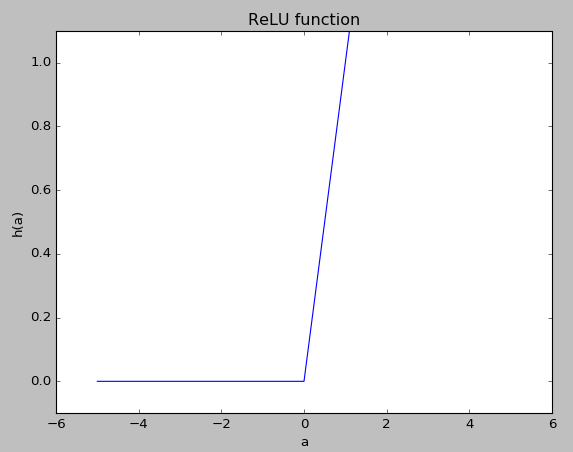
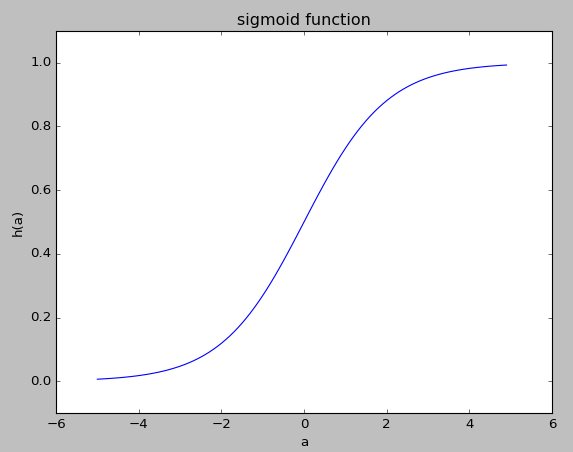
ニューラルネットワークでは、シグモイド関数やReLU関数といった微分可能な(厳密にはReLU関数は微分可能じゃないけど)関数を使うことで、より高度な学習が可能となります。
出力層の活性化関数だけはソフトマックス関数など、中間層とは異なる関数を使います。
ソフトマックス関数は、各出力結果を百分率に直すような関数です。
分類問題においては、出力層の各ノードが入力が属するクラスに対応しているため、ソフトマックス関数の各結果はそのクラスに属している確率を表します。
しかし、分類問題の場合は一番確率の高いクラスだけがわかればいいという場合が多いので、ソフトマックス関数を使わず出力層の結果で一番大きなクラスを取り出すという処理を行う場合もあります。
畳み込みニューラルネットワーク
ニューラルネットワークでは、隣接する層の入力がすべて結合する「全結合」($a$を求める処理)とその結果を次の層の入力に変換する「活性化」の2種類の層が重なり、最後に「ソフトマックス(SoftMax)」関数を使って最終的な出力を得ます。
畳み込みニューラルネットワークでは、「畳み込み」と「プーリング」という層が加わります。
畳み込みとプーリングは入力層に近い部分で使用されます。
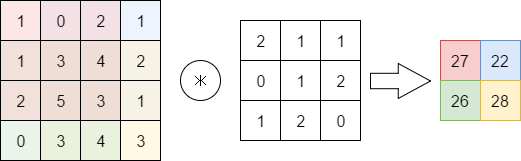
畳み込みはフィルタを各値に適用します。左上からフィルタと値の場所が対応で積和を取り、それをずらしながら適用していくことで最終的な結果を得ます。
図の通り、フィルタを適用するとデータの構造が変化してしまいます。
そこで、入力のデータを0等の固定値で埋める処理をあらかじめ行うことで、データ構造を変化させないパディングという処理を行うことが多いです。
プーリングはデータ構造を変化させるための処理です。
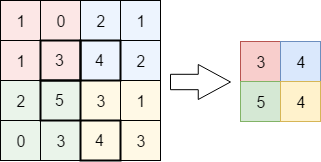
方法はいくつかありますが、範囲内の最大値を選択するMAXプーリングがよくつかわれます。
4×4のデータに対し、2×2のMAXプーリングを適用すると2×2のデータになります。
通常のニューラルネットワークでは、入力データの値だけを扱いますが、畳み込みニューラルネットワークではデータの位置も考慮します。
画像などピクセル同士の位置に密接な関連があるようなデータも多いので、畳み込みニューラルネットワークを使うことで精度を上げることができます。
ディープラーニング
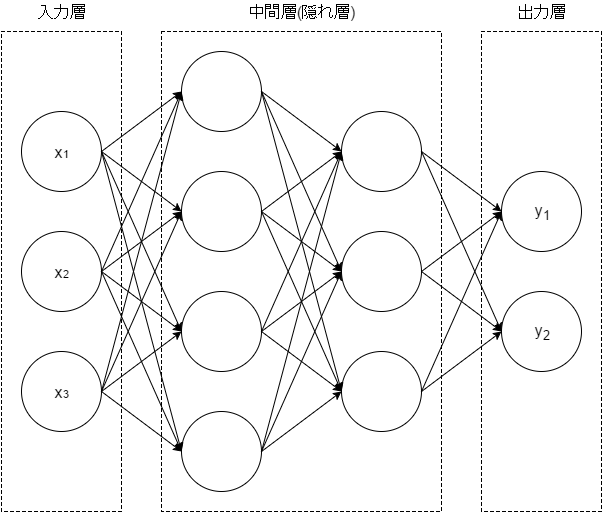
ディープラーニングは層を深くしていったニューラルネットワークです。
さらに様々なテクニックを併用することでより精度がよいネットワークを構築することができます。
例えば、ResNetと呼ばれるネットワークは150層以上の層を重ねたネットワークです。
層が増えていくと、精度が増していきますが、実行時間がかかります。
そこで、GPUコンピューティングや並列処理を実現することで処理を高速化する工夫も研究されています(GoogleのTensorFlowなど)。