最近よく聞くQuorumは過半数(多数決)よりも一般的でパワフルな概念だった

最近では珍しくもなくなった"Quorum"という言葉。Zookeeper, etcd, Serfといったクラスタ中でデータのレプリケーションを行ってくれるようなツールや、Cassandra, Riakといった分散データベース(NoSQL系)のようなツールにおいても、データの複製に一貫性を持たせる仕組みとしてよく聞かれます。

しかしながら、多くのスライドやWebの記事を読んでも、"Quorum"という語が意味するところは要するに「過半数ノードによる多数決」というような説明が多いように感じていました。

にも関わらず、"Quorum"と呼ばれているのはなぜか？そんな疑問を持っていたので、この機会に調べてみました。

そうしたら、"Quorum"は過半数/多数決という概念を一般化した非常に抽象でパワフルな概念だということがわかりましたのでここにまとめておきたいと思います。

分散システムにおけるデータの複製

最近では、珍しくもなくなってきた分散システム。分散システム上では、データは一箇所に保存されることはほぼ皆無で、複数のノードにデータがコピーされて保存される、つまり複製が複数存在することがほとんどです。

複製をすることで読込スループットを上げることができたり、複製をクライアントに返すことによって読込速度を向上させたり出来るわけですが、分散システムの持つ特徴である「耐障害性」の観点から言えば、他のノードが停止していてもデータの読込/書込ができる、つまり、データの可用性(Availability)が高まったりします。

しかしながら、それはタダでは手に入らなくて、複製が増えたら増えただけ、データの変更時に複製をうまいこと管理してやらならなくなります。複製の内容にばらつきが出たりしてしまうと、クライアントに対して、読込データの一貫性(Consistency)を提供するのが難しくなるということです。

そして分散システムにおいては、複数のプロセス群はネットワークによって隔てられているので、ネットワークが分断(ネットワーク全体がダウンしたら動かないのは自明なので)した場合にも正常に動いて欲しい(Network Partition-Tolerant)なんていう要求も出てくるわけです。

このC, A, Pという３つの性質はどうやっても３つ同時に満たすことが出来なくて、２つしか同時に満たすことが出来ないというのが2000年代はじめに証明された、有名なCAP定理です。

よく聞くQuorumって多数決/過半数でしょ？

ちょっと脱線してしまいましたが、複製の管理方法でよく聞くのが Quorum を使った方法です。(その他にも、ROWA(Read One Write All)、Primary Copy ROWAといった方法があります)

いわゆるNoSQL(Cassandra, Riak等)や、Paxos, RAFTといったアルゴリズムで有名な、分散合意アルゴリズム, リーダー選出アルゴリズムの中で使われています。

この Quorum、しばしば下記のように「過半数/多数決」を使って説明されることが、多く、「Quorum？あー多数決/過半数のことでしょ？」と理解されている事が多いのではないでしょうか？

過半数のノードによるConsistentな複製の実装は、こんな感じです。

過半数/多数決を使った複製の管理方法:

• 書込時: 過半数¹以上のノードに、タイムスタンプ²付きで書込めるまで待つ
• 読込時: 過半数のノードから複製を読み込んで、一番新しいタイムスタンプのものをクライアントに読込結果として返す

こうすると、read/writeどちらの場合にも「必ず」最新タイムスタンプのデータを得ることが保証される、という訳です。(複数同時書込を行うにはもう一工夫必要です)

しかし、これだけであれば、そもそも過半数/多数決と言えば良い所を、わざわざ"Quorum"という名前で呼んでいるということは、そこに何か違いがあるのではないかと思い、今回色々調べてみました。

今回調べた資料

色々調べた結果、下記のコースのChapter 7が非常に端的に良くまとまっていました。のでこれを主資料としてまとめます。

[Principles of Distributed Computing(Summer 2003)][podc_summer2003]³
(スイス連邦工科大学チューリッヒ校(ETH Zurich)分散コンピューティング研究グループによるコース)

Quorum とは

そもそもの定義から始めます。

定義 ノードの集合を$V = \{ v_1, v_2, ..., v_n \}$とする。quorum systemとは$V$の部分集合の集合 $\mathcal{S} \subset 2^V$ で次の条件を満たすものを言う。 quorum systemの要素をquorumと呼ぶ。

• どの２つのquorum $Q_1, Q_2$も共通部分を持つ($Q_1 \cap Q_2 \neq \emptyset$)

なるほど、過半数以上のサイズをもつノードの集合の集合というのはたしかにこのquorum systemになっているのがわかります。

過半数でなくても、quorum systemであれば必ず、quorum間に共通部分があるので過半数を使った方法は以下の方法で一般化出来ます。

Quorum Systemを使った複製の管理方法

• readとwriteで共通のquorum systemを定義する
• 書込時,読込時にはその中からquorumを一個選んで、quorumに所属するすべてのノードに書込/読込処理を行う(どれか一個でも失敗したらエラーとする)

読込と書込で同じquorum systemを使っているのがポイントです。すると、書込/読込処理毎に選ばれるquorumが違っても、かならず重複するノードが含まれるので、最新のデータを読み込むことが可能になります。

全ノードの中で、一つでもquorumが生きていれば、データは保全されるので、つまり、半分以下のノードが停止故障してしまっても、システムは継続してデータを提供しつづけられます。

Quorum Systemを使った分散ロック

quorum systemを使うと、分散ロックの実装も行うことが出来ます。やり方は単純で

• quorumを選んで、各ノードから順にlockを得る。一つでもlockが得られなかったら、それまで得られたlockをreleaseしてやり直す
• releaseするときはlockを得た時のquorumの全ノードのlockをreleaseする

だけです。ただし、lockする順番に定義がない場合、quorum間の共通部分が2以上あると、dead lockしてしまうので注意が必要です。

例えば、次のようなquorum systemを考えます($v_2, v_3$が共通部分です)。

$$V = \{ v_1, v_2, v_3, v_4 \};,; \mathcal{QS} = \{Q_1=\{v_1, v_2, v_3\}, Q_2=\{v_2, v_3 ,v_4\}\}$$

$Q_1$を選んだプロセスが$v_1$から、$Q_2$を選んだプロセスが$v_4$から逆順でlockを獲得していくような実行を行ったとすると、$Q_1$が$v_2$のlockを取った状態で$v_3$のロックを取れない、$Q_2$が$v_3$のlockを獲得している状態で$v_2$のlockが取れない、という状態が起きて永遠に処理が進まない、つまりdead lockが起きてしまいます。これを防ぐにはノードのID等で一定の順序でアクセスさせる必要があります。

一定のアクセス順序でlockを取得するようにすると、dead lockは起きないのですが、lockを取得できる効率がかなり悪くなってしまうので、もうちょっと効率的にやる方法もあります([Theorem 19.8, Principles of Distributed Computing][podc_allstars]を参照)

Quorum System 色々

quorum systemとしては、「どれをとっても重複がある」という条件しか要求していないわけなので、過半数以外にも色々なquorumが考えられるんじゃないか。

色々ありました。[テキスト][podc_summer2003]から紹介していきます。

まずはおさらい: 過半数(Majority)

$$ \mathcal{Majority} = \{ Q \subset V;|;|Q| = \lfloor n/2\rfloor+1 \}$$

過半数「以上」の集合をとってもよいかもしれませんが、quorumの条件としては、「どれも共通部分を持つ」なので、必要最小限⁴なquorum systemを考えるだけで十分です。

自明なQuorum: シングルトン(Singleton)

$$ \mathcal{Singleton} = \{ \{ v_{\cdot} \} \}$$

どれか一個のノードだけからなるQuorum Systemです。複製管理の文脈で考えると、ノードが何台あろうが、特定の一台だけに読書を集中させるということです。あまり役に立ちそうにありませんが、これも立派なquorum systemの一種です。

次から、面白いquorum systemが登場してきます。

グリッド(Grid)

$V,$のサイズ$,|V|=n,$が平方数($,\sqrt{n},$が整数)の時を考えます。そうすると、ノードは正方形に配置できます。

そこで、下記のように quorum を取っていきます($i+1$行以下の選び方は色々考えることが出来ます)。

$$ \mathcal{Grid} = \{;\{ (i\text{行全体})\cup (i+1\text{行以下から1個ずつ適当に選ぶ}) \};|; 1 \leq i \leq \sqrt{n}; \}$$

([Figure 19.2, Principle of Distributed Computing][podc_allstars])

上側は、列を固定して取った場合、下側は列が重複しないように各行から1個ずつとった場合です。$i$行全部とるところがポイントで、その他のquorumには必ず$i$行から少なくとも1個のノードが選ばれているので、quorumの条件を満たすというわけです。

後述しますが、$\mathcal{Grid}$ は故障に弱い性質というを持っています。それを解消したのが下記のB-グリッドです。

B-グリッド(B-Grid)

B-グリッドはグリッドと同じように格子状にノードを並べて考えます。$|V|=n=d \cdot h \cdot r$とします。格子の形は $h \cdot r$行$d$列の長方形です。行は$h$個のグループ(_band_と呼ばれます)に分かれていて、各_band_は$r$行持っています。各_band_内の行のことを_minicolumn_と呼びます。

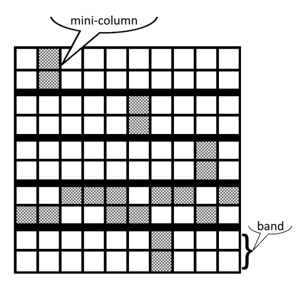
([Figure 19.3, Principle of Distributed Computing][podc_allstars])

B-グリッドにおけるquorum systemは下記のように取ります(上図参照)。

$$ \mathcal{BGrid} = \{; \{\text{全bandから一個ずつminicolumn選ぶ}\} \cup \{band ,i だけ、各minicolumnから一個ずつノードを選ぶ\} ; | ; 1 \leq i \leq h \}$$

どのquorumも、どこかのbandでグリッドの時のrowのようにすべてのcolumnを網羅していて、どのquorumも各バンドにminicolumnを持っているので、かならず共通部分が出来ます。

有限射影平面(Finite Projective Plane: FPP)

より抽象度の高い幾何学的な特性を使ったquorum systemも提案されています。射影平面と呼ばれる空間を使います。普段私達がよく知っている平面では、平行な2直線はどうやっても交わりませんが、射影平面という空間の中では任意の2直線が交わるという性質をもった不思議な空間です。

もう少し具体的に言うと、射影平面は「点の集合」「線(点の集合)の集合」「それらの接続関係」の３つで定義され、下記の3つの性質を満たす組のことを指します。

• $k^2 + k + 1$個の点と$k^2 + k + 1$個の線を持つ
• 各線は$k+1$個の点をもち、各点は$k+1$個の線に属す
• どの2つの線も一点だけを共有する
• 異なる2点を含む線はただ一つである

まったく実感がわきません。$k=2$の時で感覚を掴んでみます。下図は、位数 $k$ が 2 の場合で"Fano Plane"と呼ばれるものです。

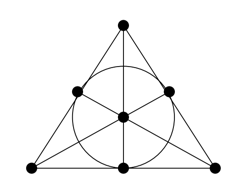
([Chapter 7, Principle of Distributed Computing(Summer 2003)][podc_summer2003])

この場合のquorum systemは「線(3つの点からなる集合)の集合」です。上の図で言うと、

• 三角形の各辺
• 各辺の中点と頂点を結ぶ3つの中線
• 各辺の中点と接する内接円(コレも線です)

どの2つの線をとっても必ず一つの点を共有できていることがわかリます。

# Quorum System の 良し悪し(評価軸) さて、色々なquorumがあるのは解りました。使え無さそうな $\mathcal{Singleton}$ から、よく使われる $\mathcal{Majority}$ , グリッドに配置したものや、小難しい射影平面と呼ばれるものもありました。

quorum systemの研究においては、「quorum systemを比べるための尺度」が幾つか提案されています。それらの尺度の定義を確認し、今回紹介したquorum systemを比較してみましょう。

負荷(Load)

直感的に言うと、各ノードがどのくらいの頻度でアクセスされるかです。定義自体は、quorumへのaccess strategy $W$によって変化するような定義になっています。

定義: $W$をquorum system $\mathcal{Q}$ 上の確率密度として、access strategyと呼ぶ。$P_W(Q)$をaccess strategy $W$を取った時に$Q$へアクセスする確率とする。

• $W$によって導かれるノード $v$ のload $l_w(v)$を下記で定義する(含まれるquorumがアクセスされる確率を全部足す)。
  $$
  l_W(v) = \sum_{Q\in\mathcal{Q}, v\in Q} P_W(Q)
  $$
• $W$によって導かれる quorum system $\mathcal{Q}$の load $L_W(\mathcal{Q})$を下記で定義する(平たく言えば一番 load の高いものを全体の load とする)。
  $$
  L_W(\mathcal{Q}) = \max_{v \in V} l_W(i)
  $$
• quorum system $\mathcal{Q}$ のload $L(\mathcal{Q})$を下記で定義する(すべての$W$の中で最小となる load の値)
  $$
  L(\mathcal{Q}) = \min_{W} L_W(\mathcal{Q})
  $$

参考: quorum system の load の下界は$1/\sqrt{n}$です。つまり、どうやっても load はコレより小さくできないということです。逆に、この値の load を持つものができたら、それは load 的に最適ということです。

耐久力(Resilience)

quorum systemがどのくらいの故障までだったら耐えうるか？という指標です。quorumを使った耐障害性は、quorum内のノードが全部生きていることが条件です。逆に言うと、1個でもquorum内のノードが停止故障していると、多のquorumと共通部分がなくなってしまうので動作が保証できなくなる。resilienceという指標は、どれだけのノードが停止してしまったら、全てのquorumが健全でなくなってしまうか？を定義したものです。

定義: quorum system $\mathcal{Q}$ の resilience $R(\mathcal{Q})$ とは、次を満たす最大の $f$ のことを言う。$V$ 中の $f$ 個のノードからなる任意の部分集合 $F$ と共通部分のないquorumが少なくとも一個は存在する。

故障確率(Failure probability)

resilienceは停止故障ノードが「何個」まで耐えられるか？でしたが、次は確率です。各ノードの稼働率を $p$ とした時のquorum systemの故障確率は次で定義されます。quorum system内のどのquorumも停止故障ノードを含んでしまう確率です。

定義: quorum system $\mathcal{Q}$の故障確率$F_p(\mathcal{Q})$は次で定義される
$$
F_p(\mathcal{Q}) = Pr[\forall Q\in\mathcal{Q},, \exists v\in Q,s.t. v\text{が停止故障している} ]
$$

今回紹介した Quoroum System の 比較

今回紹介したquorum systemを、上記のLoad, Resilience, Failure Probabilityという指標で比較してみましょう。詳細な解析はPrinciples of Distributed Computingを見ていただくとして、表にまとめると次のようになります。

quorum system	Load	Resilience	Failure Probability
Singleton	$1$	$0$	$1-p$
Majority	$>1/2$	$<n/2$	$e^{-\Omega(n)} \to 0$
Grid	$\Theta(1/\sqrt{n})$ (最適)	$\Theta(\sqrt{n})$	$(1 − p^d)^d \to 1$
B-Grid5	$\Theta(1/\sqrt{n})$ (最適)	$\Theta(\sqrt{n})$	$O(1/n) \to 0$
FPP	$\Theta(1/\sqrt{n})$ (最適)	$k \sim \Theta(\sqrt{n})$	$\to 1$

表の見方ですが、直感的には

• Load: ノードがどのくらいの頻度でアクセスされるか ➔ 小さいほどよい
• Resilience: どのくらいの故障台数まで耐えられるか ➔ 大きいほどよい
• Failure Probability: どのくらいの確率でquorum全体が使えなくなるか ➔ 小さいほどよい

それぞれ見てみます。

• Singleton: 1個しかノードを使わないのでダメダメですね。
• Majority: Resilienceがほぼ半数なのでかなり高いです。$n$ が大きくなった時の故障率もほぼ0へ漸近するのですが、Loadが $1/2$ とかなり高めです。
• Grid: Loadは最適。ResilienceもMajorityと比べると$\sqrt{n}$と小さめです。ただし、故障率が$n$が大きくなるに連れて1に近づいてしまうのでNGです。
• B-Grid: Load, ResilienceはGridと同じで、故障率も0へ漸近していくので良さそうです。
• FPP: Gridと同じです

以上を踏まえて、だいぶんざっくりとですが、◯×で上の表を書き換えてみると下記のようになるかと思います。Majorityよりも良いQuorum Systemもあることが解りますね。

quorum system	Load	Resilience	Failure Probability
Singleton	×	×	×
Majority	×	◎	◯
Grid	◎	◯	×
B-Grid5	◎	◯	◯
FPP	◎	◯	×

この表でみるとB-Gridが良さそうに見えますが、B-Gridはサイズが限られてしまう、解析においてはノードの稼働率が$1/3$以下という仮定が置かれている、等にも注意が必要です。

実践的な応用については、このリストの中だけでみるとMajorityが広く使われている理由もわかるように感じます(loadはそこそこ大きくても、resilienceが大事、またmajorityはread/writeでquorumシステムをうまく重み付けすることでread/write時のloadを調整できたりもするので)。

その他のQuorum達

今回挙げたquorum systemは基本的なものばかりです。これら以外にも様々な仕組みのquorum system達が数多く提案されています。

また、今回のquorum systemのモデルは停止故障しか考慮していませんが、分散システムを考える上で一番やっかいとされるビザンチン故障に耐性をもつByzantine Quorum Systemというものも研究されていたり、

クラシックなquorum systemは必ずintersectionが無いとダメですが、それを確率的に交わっていれば良い、と緩和したProbabilistic Quorum Systemというのも研究されています。

これらについては参照文献を参照してください。(新しめで過去の研究成果への参照がたくさん載っているサーベイ的なものを上げておいたつもりです)

まとめ

NoSQL等のOSSやプロダクトにおけるデータ整合性の設定でよく聞かれる"Quorum"というキーワード。単純に「過半数/多数決」と捉えてしまっていたのですが、調べてみると非常に奥が深く、「あーQuorumって多数決のことだよね」という理解・言及は、Quorum Systemと呼ばれるシステムの氷山の一角でしか無いことが解りましたし、分散システムにおける「動作保証」を考える上で強力なツールとなると感じました。

過半数以外のQuorumを学習して、単純明快な過半数が多のQuorumとくらべて、loadは悪いが、resilience, failure probabilityでは優れている点、またB-Gridにおいては、解析上のテクニカルな部分はあったものの、漸近的にはMajorityよりも良さそうであることが解りました。

この記事が皆さんの"Quorum　System"の理解の一助になれば幸いです。

参考文献

• "The Origin of Quorum Systems", Marko Vukolić, 2010
• "Selected Results from the Latest Decade of Quorum Systems Research", Michael G. Merideth and Michael K. Reiter, 2010
  [podc_allstars]: http://dcg.ethz.ch/lectures/podc_allstars/
  [podc_summer2003]: http://disco.ethz.ch/lectures/ss03/distcomp/
• 今回参照したテキスト
  • [Principles of Distributed Computing][podc_allstars]
  • [Principles of Distributed Computing (Summer 2003)][podc_summer2003]

1. Cassandra や RiakではreadとwriteのQuorumのサイズを別々に設定できて、データのread/writeの特性に応じたパフォーマンスを設定できたりします。 ↩

2. タイムスタンプは、いわゆる楽観ロックで使われるような、単調に増加するデータの「バージョン番号」を使うことが多いです ↩

3. リンク先にある通り、2003年時の情報なので、最新の分散システムの原理原則を包括的に学ぶなら[現行版][podc_allstars]が良いと思われます。Quorum Systemについてのみ比較すると、2003年のテキストの方が紹介されているQuorum Systemの種類多かったため、本記事ではそちらを採用しました。挿入されている図表は適宜わかりやすい方を参照しています。 ↩

4. どの２つのquorumをとっても包含関係にないという意味で必要最小限という表現を使いました。そのようなquorum systemはminimal quorum systemと呼ばれます。 ↩

5. $d=\sqrt{n},,r=\ln d,, 0\leq (1-p) \leq 1/3$としている ↩ ↩²