前回はレジスタを作ったが、その流れでプログラムカウンタを作ろう。なぜ「その流れ」かというと、プログラムカウンタはレジスタに少し手を加えたものだからだ(ということを知ったのは最近なので偉そうなことは言えないが)。
便利な二項演算子
プログラムカウンタの前に一つ。
今更感たっぷりだが、これまで論理演算はlc_andとかlc_orなど論理ゲートの処理をする関数で記述してきた。これらの関数は多入力に対応し結果もリストで返すので、複雑な論理回路の関数(lc_decorderとか)との整合性が取りやすかった([Bin]を取り[Bin]を返すから)。
しかしlc_andなど関数名が長く、ビット値をいちいちリストに変換しないといけないため、論理式が判別しにくく長くなってしまう欠点がある。
(例)
d' = lc_and ([c] ++ lc_or (lc_not [p] ++ [d]))
x2' = lc_nand ([sHI] ++ x1' ++ x3)
パッと見てどんな論理式かさっぱりだ。そこでよりすっきり書けるよう、二項演算子を定義しよう。ついでに優先度も。ちなみにNOTは単項演算子だが気にしない。(それにしても、すでに他で使われておらず、わかりやすくて短い演算子を考えるのはなかなか難しい)
-- NOT
(!>) :: Bin -> Bin
(!>) a = head $ lc_not [a]
-- AND
(&>) :: Bin -> Bin -> Bin
a &> b = head $ lc_and [a, b]
-- OR
(|>) :: Bin -> Bin -> Bin
a |> b = head $ lc_or [a, b]
-- NAND
(!&>) :: Bin -> Bin -> Bin
a !&> b = head $ lc_nand [a, b]
-- NOR
(!|>) :: Bin -> Bin -> Bin
a !|> b = head $ lc_nor [a, b]
-- XOR
(<+>) :: Bin -> Bin -> Bin
a <+> b = head $ lc_xor [a, b]
infixr 8 !>
infixr 7 &>
infixr 7 !&>
infixr 6 |>
infixr 6 !|>
infixr 6 <+>
これらを使うと、先の例は次のようにすっきり。
(before) d' = lc_and ([c] ++ lc_or (lc_not [p] ++ [d]))
(after ) d' = c &> ((!>) p |> d)
(before) x2' = lc_nand ([sHI] ++ x1' ++ x3)
(after ) x2' = (!>) (sHI &> x1' &> x3)
記述量と視認性がかなりあがった! (・・・と思う) ただし例の2つ目は、NANDがANDとNOTに代わっている。NANDの場合、二項演算子を組み合わせても3入力NANDにならないから。。。
命令の実行とクロック(立ち上がり)のタイミング
プログラムカウンタの前にもう一つ。
この記事はコードを少しずつ作りながらその状況を書いているのだが、それでも全体構成だとか、先々のロジックとかもちらほら考えながら進めている。その時にどうしても腑に落ちなかったのが、「プログラムのワンステップは電子回路のどこから始めてどこで終わるのか」ということだった。
全体の流れは、1命令について「入力があって、命令の処理をして、出力をして」というのを繰り返すのだろうが、はじめにCPUのどの構成部品に入力値を放り込んで処理を進めていくのか、というところで混乱していた。(文字で書くとなかなか説明しづらいのだが)
だが、どうすればいいか最近やっとわかった。要は、クロックのタイミングについて完全に誤解していたのだ。レジスタはクロックの直後に更新される、でもクロックが処理の発端だよねぇ、と悩んでいたわけだ。
以下に、一つの命令(ワンクロック命令とする)の処理について、これまで想像していた流れと実際の流れを示す。(クロック=クロックの立ち上がり、結果出力=レジスタ更新など)
* これまでの想像
[クロック] => (フェッチ) => (デコード) => (実行) => (結果出力)
* 実際の流れ
(フェッチ) => (デコード) => (実行) => [クロック] => (結果出力)
というわけで、一つの命令はほとんど最後まで処理されて最後の「締め」のためにクロックを待っているのだ。クロックの瞬間に結果が固定される。さらに(個人的に)驚きなのは、レジスタ値が更新されてめでたしめでたしと思っていたら、勝手に次の命令をどんどん処理していて結果も出ていて、あとはレジスタなどへの書き込み待ち、というところまでノンストップで進めてしまっていること。。。
コンピュータやCPUに詳しい方には至極当然のことだろうが、うーん、この歳になって目から鱗だった。
プログラムカウンタ
本題に入ろう。CPUの構成要素にプログラムカウンタ(以後PCとする)がある。これは、次に実行する命令の番地を記憶しておく場所だ。普通、命令が一つ実行されるとPCが1(もしくは命令長に応じた分だけ)カウントアップされる。次の命令を指すようになるわけだ。ちなみにジャンプ(分岐)命令は、PCの値を強制的に別の値(番地)に変更するもの。
さて、PCに必要な機能は次の通り。(ちなみにTD4の命令は全て1バイト)
- 命令が実行される(=クロックが入る)と次の番地を指す
- 外から番地を指定することもできる
一方で前回作ったレジスタはどうだったかというと、
- クロックが入ると前の値を保持し続ける
- 外から値を指定することもできる
という動作をする。つまりPCとは、「保持する値がクロックのたびに1ずつ増えていくレジスタ」であることがわかる。こうなればどのように作れば良いか見えてくる。
1ずつ増えていくのだから、入力に対し1増えた値を出力すればよい。4 bitのPCの場合、入力を$A_n$、出力を$Q_n$とすると真理値表は次の通り。数を強調するため、HI/LOではなく1/0で表す。なお、これまでと同じく$A_0$($Q_0$)がLSB、$A_3$($Q_3$)がMSBとする。
| $A_3$ | $A_2$ | $A_1$ | $A_0$ | $Q_3$ | $Q_2$ | $Q_1$ | $Q_0$ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
この表から、各$Q_n$を$A_n$で表せばいいわけだ。カルノー図を描いてごにょごにょ式変形すると、結果として下記の式を得る。
$
Q_0 = \overline{A_0}
$
$
Q_1 = A_1 \oplus A_0
$
$
Q_2 = A_2 \oplus (A_1 \cdot A_0)
$
$
Q_3 = A_3 \oplus (A_2 \cdot A_1 \cdot A_0)
$
ちなみに$\oplus$は排他的論理和(XOR)だ。これを使わずAND/ORで構成している回路図もあったが、XORを使うほうがすっきりして解りやすいと思う。最初の回で作った論理ゲートにXORは無いので、以下の通り追加しよう。ただし他のゲートと違い、このXORゲートは2入力に限定する。ついでに二項演算子も定義。
lc_xor :: LogicCircuit
lc_xor (a:b:_) = [(a &> b') |> (b &> a')]
where
a' = (!>) a
b' = (!>) b
(<+>) :: Bin -> Bin -> Bin
a <+> b = head $ lc_xor [a, b]
infixr 6 <+>
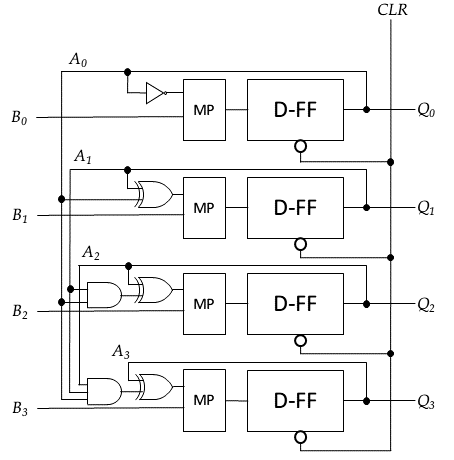
さて、先に書いたようにPCとレジスタはかなり似ている。繰り返しになるが、レジスタだと「前の(同じ)値を記憶する」ところを「値が1増える」ようにすればPCになるのだ。であれば、レジスタの入力のところにちょっと追加してやって「次の値」が入るようにすればいい。前の値からどのように作るかは上記の$Q_n$の式のとおりだ。というわけで、PCの回路図は次の通りとなるだろう。
ラッキーなことに(?)、Flip Flopの回で書いたように順序回路の「記憶」は関数の外で管理することにした。出力値を次の入力に回すことにした、というアレ。だから、出力された値をそのまま次の入力に回す代わりに、「ちょっといじった値」にして入力してやれば、レジスタ(関数lc_register4)がそのまま使えるということだ!なのでPCは簡単に作れてしまった・・・。
{- |
Program Counter (4 bit)
IN : [!CLR,!LD,A0,A1,A2,A3,B0,B1,B2,B3]
OUT: [Q0,Q1,Q2,Q3]
An: current count value
Bn: count value set by outer
Qn: next count value
-}
lc_counter4 :: LogicCircuit
lc_counter4 (c:l:ds) = lc_register4 ([c, l, d0, d1, d2, d3] ++ b)
where
bw = 4
[a0, a1, a2, a3] = take bw ds
b = take bw $ drop bw ds
d0 = (!>) a0
d1 = a1 <+> a0
d2 = a2 <+> (a1 &> a0)
d3 = a3 <+> (a2 &> a1 &> a0)
テストをするとちゃんと1つカウントアップした値が出てくる!論理回路とは、げに不思議なものだ(笑)。
まとめ
今回で「記憶」に関わる部分はあらかた出来上がったと思う(キャリーフラグが残っているが、単なるD-FFだし)。次回からいよいよ計算(命令)のロジックに入ろうと思う。
(ここまでのソース)
※ 最新のソースは執筆時点と異なっているところがある。