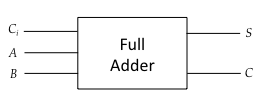
今回はCPUの中でも「純粋に」計算するところ、加算器を作ろう。ALUを作る!と行きたいところだが、残念ながらTD4(しつこいようだが「CPUの創りかた」本で製作されるCPU)では加算器しかないので今の所は諦めよう。
1 bit 全加算器
ものの本では半加算器から説明されるようだが、どうせ使わないので最初から全加算器を作る。まずは1 bitから。
入力は、2つの値$A$と$B$、あとくり上がり$C_i$(carry)の3つ、出力は加算の結果$S$と上の桁へのくり上がり$C$だ。
真理値表は次のようになるだろう。以下の説明では従来のHI、LOの代わりに1と0を使うことにする。
| $A$ | $B$ | $C_i$ | $S$ | $C$ |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
例によって、これをSとCについてそれぞれカルノー図を描いて考えると、最終的に以下のように表される(面倒なので途中の計算は省略する)。
$
S= C_i \oplus (A \oplus B)
$
$
C= A \cdot B + C_i \cdot (A \oplus B)
$
コードはこの式をそのまま表してみた。
{- |
1 bit full adder
IN : [Ci,A,B]
OUT: [S,C]
Ci : carry in
A,B : value
S : answer
C : carry out
-}
lc_adder1 :: LogicCircuit
lc_adder1 (ci:a:b:_) = [s, c]
where
a_xor_b = a <+> b
s = ci <+> a_xor_b
c = (a &> b) |> (ci &> a_xor_b)
全加算器は大した回路ではないので、テストもすんなりと通った。
>>> lc_adder1 [sLO, sLO, sLO] == [sLO, sLO]
True
>>> lc_adder1 [sLO, sLO, sHI] == [sHI, sLO]
True
>>> lc_adder1 [sLO, sHI, sLO] == [sHI, sLO]
True
>>> lc_adder1 [sLO, sHI, sHI] == [sLO, sHI]
True
>>> lc_adder1 [sHI, sLO, sLO] == [sHI, sLO]
True
>>> lc_adder1 [sHI, sLO, sHI] == [sLO, sHI]
True
>>> lc_adder1 [sHI, sHI, sLO] == [sLO, sHI]
True
>>> lc_adder1 [sHI, sHI, sHI] == [sHI, sHI]
True
4 bit 加算器
1 bit 全加算器ができたので、これを数珠つなぎにすれば$n$ bitの加算器を作ることができる。本CPU(TD4)はレジスタが4 bitなので4 bit 加算器を作ろう。言わずもがなだが、全加算器を次のようにつなげれば良い。入力$A_n$、$B_n$および$C_i$、出力が$S_n$と$C$だ。
よって、先に作った全加算器(lc_adder1)をこの図のとおりにつなげて計算すればよいのだが、数珠つなぎだからこれは再帰で表現できそうだ。まず再帰処理の本体から考える。入力は$n$ bitの$A$と$B$だが、それらの同じ桁の値を組にしたリストを用意しよう。これを順に加算器に入れ、各桁の結果$S_i$を求めたい。大雑把には次の通り。
[(a0,b0), (a1,b1), ... , (an,bn)] → [s0,s1, ... , sn]
ただし、くり上がり(carry)があるので少々複雑になる。くり上がりも含め計算するために、その桁に足し込みたいcarryも引数で与える。さらに、計算結果$S$を次に渡していくので、これも引数にする。これらを踏まえると、つぎのような関数adder_nができる。
{-
IN : Ci, [Si], [(Ai,Bi)]
OUT: [Si,C]
Ci : carry in
Ai, Bi: value
Si : Answer
C : carry out
-}
adder_n :: Bin -> [Bin] -> [(Bin, Bin)] -> [Bin]
adder_n ci ss [] = [ci] ++ ss
adder_n ci ss ((a, b):ds) = adder_n c (s:ss) ds
where
[s, c] = lc_adder1 [ci, a, b]
$A$と$B$の各桁の組のリストを先頭から一組取り出して、carryと合わせて加算する。残りのリストと計算結果を使ってadder_nを呼出す(再帰)。処理するリストがなくなったら、$S$の前に最後のくり上がりを追加して終わり。この関数では「最後の桁」が先頭に来るから、出来上がった$S$のリストは逆順にしないといけない。加算器の出力は、$S_n$,$C$の順にしたいので、再帰の終端で最後のくり上がりを「先頭に追加」したわけだ。
あとは、このadder_nを呼び出す「外側」の関数を作れば良い。lc_adderとする。
先のadder_nの出力を逆順にしたら以下のようになる。
[s0,s1, ... , sn, c]
これを踏まえてコードにすると次の通り。
{- |
n bit full adder
IN : [A,B]
OUT: [S,C]
A,B : value
S : answer
C : carry out
-}
lc_adder :: LogicCircuit
lc_adder ds = reverse $ adder_n sLO [] $ zip a b
where
l2 = length ds `div` 2
a = take l2 ds
b = drop l2 ds
加算器のビット数を明示的に与えていないことに注意。ビット数は、入力(リスト)の長さの半分とした。$A_n$と$B_n$が繋がったリストで入力される前提だ(4 bitなら要素は8個のはず)。奇数個だったら余りは無視される。これで$n$ bit加算器の完成だ。テストも上々だ(長くなるので割愛)。
まとめ
今回は少々軽めの内容だったが、「一番計算機らしい回路」と言えなくもない(?)加算器を作った。先述の通りこのCPUは加算器しか持たないので乗算器などに手は出さないが、将来CPUをパワーアップするとしたら要検討かもしれない。
これでCPUで必要となる論理回路のモジュールがほぼ出揃った。あと残すは「本丸」の命令デコーダのみだ。だが次回はその前にCPUの全体構成を確認したいと思う。その方が命令デコーダの作り方がよく分かるとおもうから。
(ここまでのソース)
※ 現在のソースは執筆時点から変更されている場合あり。