レイトレーシング(10): 拡散反射と面光源

DeepLearning回からだいぶ間があき、さらにレイトレーシングは1年半以上も時間が空いてしまった。それは拡散反射でとある処理の解法で壁にぶつかっていたからだ。それが非常に簡単に解決できるとわかったのでちょっと進めることにした。

0. 前回まで

前回までで、フォトンマッピング法を用いたレイトレーシングプログラムを作成した。といってもフォトン追跡は何か物体にぶつかったらそれでおしまい、反射は未対応という中途半端な状態だ。

久しぶりなので気分を一新して新しいシーンに変えてみよう。実はこのページのパクリだ。ちなみにこの連載は知りたいことが多く書いてありとても参考にさせていただいている。売り物の3DCGソフトを使っての説明だが理論的なところが詳しくよくわかる。

さて、前回までで作ったフォトンマッピングプログラムと古典レイトレーシングで描画したものがこちら。

一目瞭然、フォトンマッピングのほうは影がぼやけてしまう。点光源なので影は古典のようにくっきりとした縁、かつ真っ黒でなければならない。前の記事でも書いたがフォトンマッピングはある点の周囲のフォトンを集計して輝度を計算するので、影のなかにフォトンがないと収集する範囲を広げてしまうのだ。

ということでさらの前回のおさらいだが、フォトンを収集する範囲を限定して描画してみる。設定は0.2 [m]だ。それより外のフォトンは無視して輝度を判定する。

残念ながら影の縁はぼやけてしまうが、上の画像よりははるかに本物っぽい。今後はひとまずフォトンの収集範囲を0.2 [m]として、色々試すことにしよう。ちなみにフォトン数は20万個、これでも残念ながら"まだら模様"になるのは今は我慢しよう。

なおフォトンマッピングと古典レイトレーシングでは輝度の計算方法が全く異なるわけだが、両者の明るさや色の加減はほぼ同等であることに注目したい。レイトレーシングといっても要するに物理（光学）シミュレーションなので同じ設定なら（ほぼ）同じ結果が出てこないといけないのだ。その点で、ひとまず両者のプログラムに大きな間違いはなさそうだ。

1. 拡散反射の実装

さて本題の拡散反射である。現時点ではシーン中の全物体は完全拡散反射面としているので、フォトンを追跡して物体にぶつかったらフォトンマップに記録し、別方向へ反射させればよい。ところが長い間詰まっていたのはその反射方向をどうするか、であった。

(1) 拡散反射ベクトルの生成法

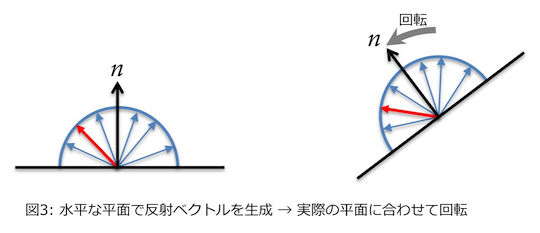
完全拡散反射面ではフォトンが物体にぶつかるとその面の半球状のいずれかに等確率で反射する。当初は、まず上方向の平面を考え、半球のどこかへ向かうベクトルを求めてからそれを法線方向によって回転させようとした。

反射ベクトルは点光源でフォトンをランダムに生成した経験から、それを上半分だけに限定すれば生成できる。あとは回転だが、回転行列を作るのか四元数を使うのか、よく分からないまま止まっていた。一般的にどうしているのか検索もしてみたがどうもそれらしい情報を見つけられない。

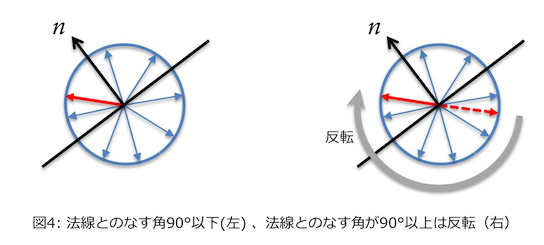
で、先日極めて容易に生成できる方法に気がついた。球状のランダムなベクトルを生成したあと、求めたい面の法線とのなす角が90度以下ならそのまま採用、90度以上なら反転させればいいのだ。

なんと簡単なことに長時間悩んだことか、恥ずかしくなるぐらいだ。。。この処理をコードにすると次の通り。generateRandomDir?は以前作っていたもの(生成方法により四種類あり、?はその番号、一例として四番目を示す)。

Algebra.hs

generateRandomDir4 :: IO Direction3
generateRandomDir4 = do
  y' <- MT.randomIO :: IO Double
  p' <- MT.randomIO :: IO Double
  let y = y' * 2.0 - 1.0
      p = p' * 2.0 * pi
      r = sqrt (1 - y * y)
      x = r * (cos p)
      z = r * (sin p)
      v = initPos x y z
      len = norm v
  return $ fromJust $ normalize v

diffuseReflectionが反射ベクトルの生成だ。

Geometry.hs

diffuseReflection :: Direction3 -> IO Direction3
diffuseReflection n = do
  d <- generateRandomDir4
  let cos = n <.> d
  return $ if cos > 0.0 then d else negate d

こんなたった数行でできることに悩まされていたとは・・・。

(2) フォトン追跡をいじる

反射ベクトルを作ることができたので、フォトン追跡にも手を入れよう。従来の追跡処理は次のようであった。

• フォトンの進行方向にある物体についてその距離を取得する
• フォトンより前にあるものの中から最も近いものを選びPhotonCacheとして返す

コードはこちら。

tracePhoton :: [Object] -> Photon -> IO [PhotonCache]
tracePhoton os (wl, r) = do
  let iss = filter (\x -> fst x > nearly0) (concat $ map (calcDistance r) os)
      (t, s) = head $ sortBy (comparing fst) iss
  return [(wl, initRay (target t r) (getDir r))]

ここは大幅に変更している。やりたいことは次の通り。

• フォトンがぶつかる最初の物体との交点を得る(calcIntersection)
• ぶつからなければ空リストを返す。
• ロシアンルーレット法を使い物体の反射率以下なら反射(reflect)し さらにフォトン追跡をしてPhotonCache情報を得る。
• 反射率以上ならフォトンが吸収されたとして追跡を止める。
• 交点が拡散反射面(*1)ならその点のPhotonCahce情報を作成する。
• 交点および反射方向から全PhotonCache情報を集めて返す。

(*1)について、今は拡散反射面という前提だが、将来の拡張のためこのような判定を入れている。上記処理のコードは次の通り。

Tracer.hs

tracePhoton :: [Object] -> Int -> Photon -> IO [PhotonCache]
tracePhoton os l (wl, r) = do
  let is = calcIntersection r os
  if is == Nothing
    then return []
    else do
      let (p, n, m) = fromJust is
      i <- russianRoulette wl [reflectance m]
      pcs <- if i > 0
        then reflect p n os l wl
        else return []
      if diffuseness m > 0.0
        then return $ ((wl, initRay p (getDir r)) : pcs)
        else return pcs

reflect :: Position3 -> Direction3 -> [Object] -> Int -> Wavelength
        -> IO [PhotonCache]
reflect p n os l wl = do
  dr <- diffuseReflection n
  let r' = initRay p dr
  pcs <- tracePhoton os (l+1) (wl, r')
  return pcs

なお、後々の拡張のため、反射回数を引数に追加している(l)。ちなみにrussianRouleteはこのようになっている。

Physics.hs

russianRoulette :: Wavelength -> [Color] -> IO Int
russianRoulette wl cs = do
  r <- MT.randomIO :: IO Double
  return $ rr wl cs 0.0 r (length cs)

rr :: Wavelength -> [Color] -> Double -> Double -> Int -> Int
rr _ [] _ _ len = len
rr wl (c:cs) c0 r len
  | r < c'    = len
  | otherwise = rr wl cs c' r (len - 1)
  where
    c' = c0 + selWl wl c
    selWl :: Wavelength -> Color -> Double
    selWl Red   (Color r _ _) = r
    selWl Green (Color _ g _) = g
    selWl Blue  (Color _ _ b) = b

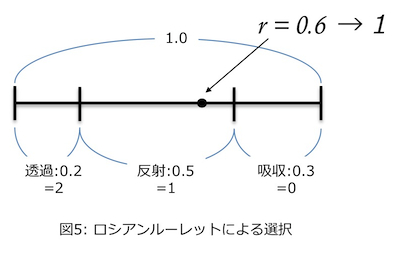
まず[0,1]の一様乱数rを作り、Colorのリストから指定の波長の値を取り出してそのrを上回ったところでリスト要素の順番(逆順)を返す。分かりにくいので例を示す。物質の反射率、透過率が次のようであったとする。ただし各色の反射率+透過率は1.0を超えない。

反射率: 赤=0.5、緑=0.1、青=0.6
透過率: 赤=0.2、緑=0.6、青=0.4

1.0-(反射率+透過率)は吸収率だ。ここで赤を例に判定しよう。その場合、リスト[Color]は[[0.2,0.6,0.4],[0.5,0.1,0.6]]である。赤について取り出すと[0.2,0.5]だ。rが0.6であれば、

• 1番目の透過率=0.2と比べるとrが大きいので次へ
• 2番目の反射率=0.5だが先の0.2とあわせて0.7としてrと比較すると、 今度はrが小さいので、この時の要素数1を返す

ということで1になる。

もしrが0.1なら1番目の透過率0.2より小さいので結果は2なわけだ。この番号は、先のフォトン追跡の際に吸収、反射、透過のどれかを表すのに使っており、このプログラムでは0=吸収、1=反射、2=透過と決めた。なので、russianRouletteの返値が0より大きければフォトンを反射してさらに追跡するようにしている。

      i <- russianRoulette wl [reflectance m]
      pcs <- if i > 0
        :

さて、それでは次に画像を生成してみよう。

(3) 間接光の効果はすごい

拡散反射を実装したので、あらためてフォトンマップを生成する。

$ cabal build
  :
$ dist/build/pm/pm > scene1.map
$ dist/build/rt/rt < scene1.map > scene1.ppm

以下に、機能拡張したプログラムで生成した画像と比較のため直接光のみの画像および古典版を示す。古典版はいわゆる「環境光」に2 [mW/m^2/sr]の輝度を与えた。

結果は明らかだ。まだら模様と影の縁がぼやけているのは仕方ないとして、

• 球の下の方は床からの照り返しでほんのり明るくなっている
• 球の左右はそれぞれ赤・青の壁からの反射で少し赤み・青みがかっている
• 天井も壁からの照り返しがある

など、だいぶリアルな画像が得られたと思う。まだら模様もまあいわゆる「味わい」と言えなくもない（と自分を慰めてみる）。

2. 面光源も

さて、拡散反射による間接光が思いの外いい効果を出したので、もう少し拡張してみる。先の例では点光源なのに影の縁がぼやけていた。でも大きさのある光源ならぼやけていて当たり前、違和感がないはず？

まずは実装が簡単そうな平面光源を追加してみる。

(1) 平面光源

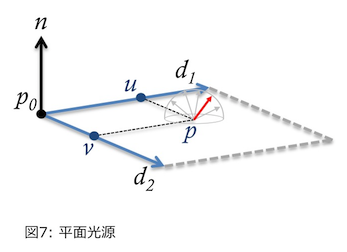
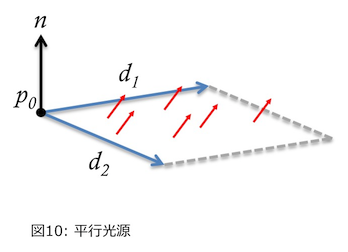
点光源は一点から球状のあらゆる方向へフォトンが放射されるが、面光源は面のそれぞれの点から半球状に放射される。そう、拡散反射の実装で拡散反射ベクトルを求めたがそれがそのまま使える。あとは平面をどう定義するかだが、あまり手をかけたくないので2つのベクトル($\boldsymbol{d_1}$, $\boldsymbol{d_2}$)で表される「平行四辺形」にしたいと思う（下図）。

フォトンの放出方法だが、まず面光源のどこから放出されるかを2つの一様乱数($0 \leq u \leq 1$, $0 \leq v \leq 1$)で決める。放出点を $p$ とすると、

$
\boldsymbol{p} = \boldsymbol{p_0} + u \cdot \boldsymbol{d_1} + v \cdot \boldsymbol{d_2}
$

となる。あとは拡散反射と同様に半球状のランダムな方向ベクトルを生成してフォトンを飛ばしてやれば良い。コードにするとこんな感じ。

Light.hs

data Light =
  PointLight
    { lcolor :: Color
    , lflux  :: Flux
    , pos    :: Position3
    }
  | ParallelogramLight
    { lcolor :: Color
    , lflux  :: Flux
    , pos    :: Position3
    , nvec   :: Direction3
    , dir1   :: Direction3
    , dir2   :: Direction3
    }

generatePhoton (ParallelogramLight c _ p n d1 d2) = do
  wl <- MT.randomIO :: IO Double
  t1 <- MT.randomIO :: IO Double
  t2 <- MT.randomIO :: IO Double
  d  <- diffuseReflection n
  let r = initRay (p + t1 *> d1 + t2 *> d2) d
      w = decideWavelength c wl
  return (w, r)

生成してみたフォトンマップがこちら。天井に黒い四角が見える。これが面光源。

さて、これを使ってレイトレーシングしたいのだが、問題は大きさのある光源の場合「目に見える」ということだ。点光源は大きさがないので無視していたが、今度はそうはいかない。なのでレイトレーシング時に他の物体と同じように交差判定とかしてやらないといけない。というか本来は逆だ。物体がたまたま光を放出しているから光源なのだ。というわけで、物体の表面属性に「発光」を加えてやろう。他にも今後対応する（かもしれない）反射・透過関係も入れて、次のように定義した。

Material.hs

data Material = Material
  { reflectance   :: Color
  , transmittance :: Color
  , specularRefl  :: Color      -- specular reflectance
  , emittance     :: Radiance
  , ior           :: Color      -- index of refraction
  , diffuseness   :: Double     -- 拡散性
  , smoothness    :: Double
  } deriving Eq

このemittanceがそれだ。ここまでくると、物体定義を使って光源としての処理をしてやるのが筋ってもんだ、と思う。つまりLight型を物体と別に定義するのではなく物体を使ってフォトン放出をするということだ。が、ちょっと手間なので今回は割愛、今後のがんばりに期待。

で、代わりに「平行四辺形」という物体を定義してやろう。

Geometry.hs

data Shape = Point !Position3
           | Plain !Direction3 !Double
           | Sphere !Position3 !Double
           | Parallelogram !Position3 !Direction3 !Direction3 !Direction3
           deriving Eq

Parallelogramがそれ。あとは他の物体と同じく各関数を定義してやる。

Geometry.hs

getNormal p (Parallelogram _ n _ _) = Just n 

distance r@(pos, dir) (Parallelogram p n d1 d2)
  | res == Nothing = []
  | otherwise      = [t]
  where
    res = methodMoller 2.0 p d1 d2 pos dir
    (u, v, t) = fromJust res

ポリゴンの当たり判定はこのページを参考にさせていただいた。「Tomas Mollerの交差判定」だそうだ。これを次のように定義した。

Geometry.hs

methodMoller :: Double -> Position3 -> Direction3 -> Direction3
             -> Position3 -> Direction3
             -> Maybe (Double, Double, Double)
methodMoller l p0 d1 d2 p d
  | detA == 0.0        = Nothing
  | u < 0.0 || u > 1.0 = Nothing
  | v < 0.0 || v > 1.0 = Nothing
  | u + v > l          = Nothing
  | otherwise          = Just (u, v, t)
  where
    re2 = d <*> d2
    detA = re2 <.> d1
    p'   = p - p0
    te1  = p' <*> d1
    u    = (re2 <.> p') / detA
    v    = (te1 <.> d)  / detA
    t    = (te1 <.> d2) / detA

なお、もともとは三角ポリゴンの判定に使うもので、計算される $u$, $v$ は

$
0 \leq u \leq 1, 0 \leq v \leq 1
$

$
u + v \leq 1
$

を満たす必要がある。しかし今回は平行四辺形の当たり判定をしたいので、

$
0 \leq u \leq 1, 0 \leq v \leq 1
$

$
u + v \leq 2
$

とした。そのため以下のように謎の"2.0"が入っているのだ。

    res = methodMoller 2.0 p d1 d2 pos dir

さあ、準備は整った。画像を生成してみよう。

$ dist/build/pm/pm > scene2.map
$ dist/build/rt/rt < scene2.map > scene2.ppm

生成された画像と同じシーンを古典で生成したもの、および点光源の画像を並べてみる。

まあ正直なところこの程度の平面光源では点光源と大差ないのだが。

(2) 平行光源=太陽光

このまま勢いに乗って平行光源に手を出そう！典型的な平行光源は「太陽」だが、その特徴は一方向にしかフォトンが放出されないことだ。太陽は地球から見れば点光源のようなものだが、あまりに遠いので地球上ではフォトンの放射方向が(ほぼ)一方向になってしまう。古典レイトレーシングでは大きさをもたずあらゆる場所で光が届いているか判定するのだが、フォトンマッピングでは光源の範囲を制限してやらないと無限にフォトンを放出しなければならなくなってしまう。ということで今回はちょっとせこい手だが「面光源から一方向にのみフォトンが放出される」ものを平行光源とすることにした。イメージは「窓から入り込む太陽光」だ。

とすれば実装は平行光源のそれを参考に比較的簡単にできあがる。

Light.hs

data Light =
  (中略)
  SunLight
    { lcolor :: Color
    , lflux  :: Flux
    , pos    :: Position3
    , nvec   :: Direction3
    , dir1   :: Direction3
    , dir2   :: Direction3
    , ldir   :: Direction3
    }

SunLightがそれ。以下、各関数の定義を示す。

Light.hs

generatePhoton (SunLight c _ p n d1 d2 d0) = do
  wl <- MT.randomIO :: IO Double
  t1 <- MT.randomIO :: IO Double
  t2 <- MT.randomIO :: IO Double
  let r = initRay (p + t1 *> d1 + t2 *> d2) d0
      w = decideWavelength c wl
  return (w, r)

getDirection (SunLight _ _ lp n d1 d2 dt) p
  | cos > 0.0      = []
  | res == Nothing = []
  | otherwise      = [t *> dt']
  where
    d = lp - p
    cos = n <.> d
    dt' = negate dt
    res = methodMoller 2.0 lp d1 d2 p dt'
    (u, v, t) = fromJust res

getRadiance l@(SunLight (Color r g b) f _ _ _ _ _) (d:ds) =
  (Radiance (r * f) (g * f) (b * f)) : getRadiance l ds

generatePhotonは、面のどこからフォトンが放出されるかをランダムに決めたらあとは指定した一方向へ放出している。getDirectionはややこしそうだが、実のところ平行四辺形からその地点へ光が放出されるかどうか、放出方向へ向かって交差判定しているのだ。なおこの光源も「目に見える」が、窓という想定で空色にしておこう。

これで平行光源の定義もできた。画像を生成してみよう。また、フォトン数を20万個から30万個に増やした時の画像も示す。まだら模様がいくぶん緩和されているのがわかる。影も滑らかで本物っぽい！

古典と比べるとその効果は歴然である。古典では間接光が表現できずボールの形すら認識できない。一方フォトンマッピングでは間接光により壁やボールがやんわりと照らされ形になっている!これこそフォトンマッピングの醍醐味と言えるだろう。ただ、直接壁に当たる光については輪郭がぼやける。これは点光源での影と同じである一定の範囲のフォトンを収集してしまうため「直射日光」の当たる少し外側も引っ張られて非常に明るくなってしまうのだ。フォトンマップ（下図）では輪郭がくっきりしているので、やはり収集方法の問題だ。

とはいえ、平行光源については概ね満足できる結果といえよう。

3. まとめ

やっと拡散反射を実装できた。手間取ったが、拡散反射により得られる間接光にはそれだけの効果がある！とくに閉じた部屋へ太陽光(平行光源)が入射した時の表現は思った以上に綺麗で（個人的には）感動ものだった。

次回は画質の向上をねたにしよう。

---

ここまでのソースはこちら。