またもWikiBookのUnityチュートリアルからです。
ほぼ翻訳もの。記事はこちら「GLSL Programming/Unity/Silhouette Enhancement」
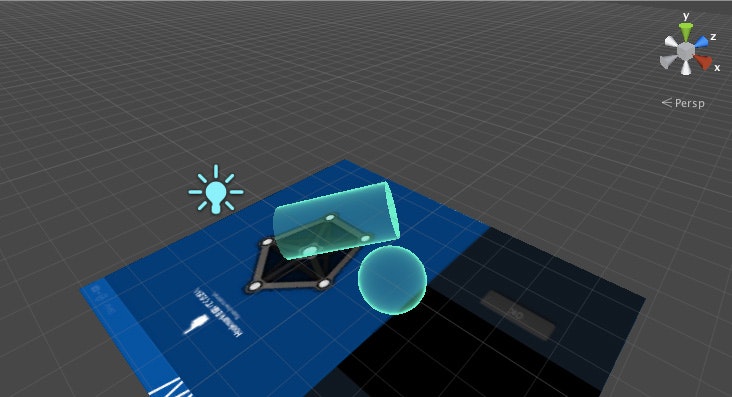
実際に適用してみると以下の感じになります。
シェーダソースは以下。
Shader "Custom/Silhouette" {
Properties {
_Color ("Color", Color) = (1, 1, 1, 0.5)
}
SubShader {
Tags { "Queue" = "Transparent" }
Pass {
ZWrite Off
Blend SrcAlpha OneMinusSrcAlpha //標準的なアルファブレンディング
GLSLPROGRAM
//シェーダ用にシェーダプロパティを定義
uniform vec4 _Color;
//ワールド座標系のカメラの位置
uniform vec3 _WorldSpaceCameraPos;
//Model matrix
uniform mat4 _Object2World;
//Model matrixの逆行列
uniform mat4 _World2Object;
//正規化された表面の法線ベクトル
varying vec3 varyingNormalDirection;
//正規化されたビュー方向ベクトル
varying vec3 varyingViewDirection;
#ifdef VERTEX
void main()
{
//unity_Scale.wの乗算は不要です。
//なぜならベクトルを正規化するためです。
mat4 modelMatrix = _Object2World;
mat4 modelMatrixInverse = _World2Object;
varyingNormalDirection = normalize(vec3(vec4(gl_Normal, 0.0) * modelMatrixInverse));
varyingViewDirection = normalize(_WorldSpaceCameraPos - vec3(modelMatrix * gl_Vertex));
gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}
#endif
#ifdef FRAGMENT
void main()
{
vec3 normalDirection = normalize(varyingNormalDirection);
vec3 viewDirection = normalize(varyingViewDirection);
float newOpacity = min(1.0, _Color.a / abs(dot(viewDirection, normalDirection)));
gl_FragColor = vec4(_Color.rgb, newOpacity);
}
#endif
ENDGLSL
}
}
}
ここで行っていることの概要を説明すると、そもそも、半透明のものを実際に見てみると輪郭部分が一番不透明になり、結果輪郭がしっかりします。
それを計算によって表現しよう、というのがこの内容です。
具体的には、表面(surface)の法線方向と視点方向の内積を取り、その結果を元に透明度を変化させる、というものです。
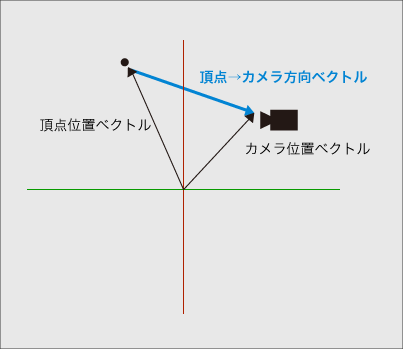
まず、各頂点をワールド座標変換してワールド座標系に置き、視点ベクトルとの差分から頂点→視点のベクトルを算出します。
(normalize(_WorldSpaceCameraPos - vec3(modelMatrix * gl_Vertex))の部分)
これで、各頂点に置ける視点方向へのベクトルが得られました。
次に求めるのは法線のワールド座標系での方向です。
法線のワールド座標系への変換行列は、通常のモデルの変換行列の逆転置行列になるので、_Object2Worldではなく、_World2Object行列を使います。
(詳細についてはこちらの記事が参考になります→法線の変換の話)
よって、normalize(vec3(vec4(gl_Normal, 0.0) * modelMatrixInverse));を計算すれば求まります。
上記2点をvarying変数からフラグメントシェーダに送ります。
あとはこのふたつのベクトルを利用して、輪郭部分に近づくほど透明度が下がるよう計算してやれば終わりです。
具体的なコードは
float newOpacity = min(1.0, _Color.a / abs(dot(viewDirection, normalDirection)));
の部分ですね。
abs(dot(viewDirection, normalDirection))の部分で視点方向のベクトルと法線ベクトルの内積(dot)を計算し、さらにその絶対値を取ります。
絶対値にする理由は、求めたいものがふたつのベクトルがどれだけ直行しているか、という点のためです。(内積の結果は直行していると0になる。つまり、0に近づくほど視点方向ベクトルと直行するようになり、つまり輪郭に近づいていく、ということです)
さらにそれで求まった数値で、設定しているカラーのアルファ値を割ることで、逆に視点方向に向いている法線ベクトルの位置を透明に、輪郭に近づくに連れて不透明になっていく、というのを実現しています。