全体的な内容についてはこちらの記事(考えるほどにブラックボックス化してくるスキンメッシュアニメーションを解説)と、こちらの記事(その61 完全ホワイトボックスなスキンメッシュアニメーションの解)を参考にさせて頂きました。
今回も例によって、サンプルをjsdo.itに上げてあります。
スキニングメッシュという名の通り、モデルのスキン、つまり皮膚を表現する技術です。
それを実現するのがボーン、というわけですね。
ざっとした流れ
ざっとした流れを書くと、
- 親子関係を持ったボーン郡を生成する
- ボーンの初期姿勢を計算しておく
- ボーンを動かす(差分姿勢)
- 動いた差分と重み付けを使ってどれくらい皮膚(つまり頂点)を動かすかを計算する
- あとは通常のレンダリング
という流れです。
この流れを、順を追って見ていきます。
ポリゴン設計
上記参考にさせて頂いた記事の設計を、今回はそのまま使わせてもらいました。
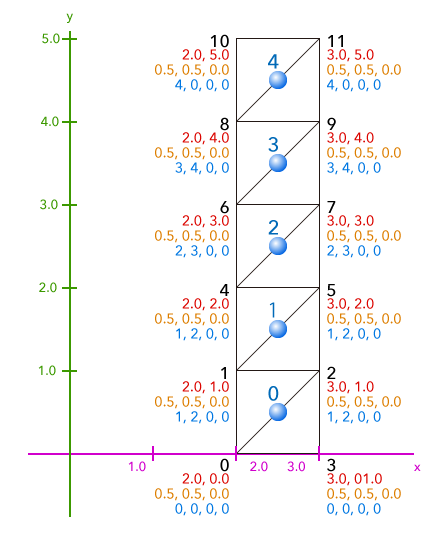
ポリゴンの頂点位置(赤)と、ボーンの重み付け(オレンジ)、そして影響を受けるボーンのインデックス(青)です。
球体の上に書かれているのはボーンのインデックスです。
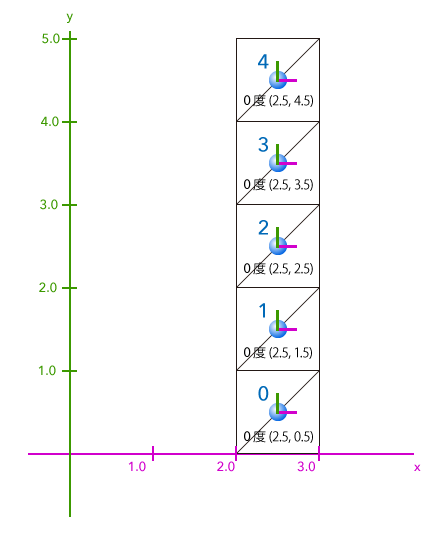
こちらはボーンの絶対座標による位置と回転角度です。(すべて0度)
今回は上記のように、非常にシンプルなポリゴン構成です。
板が5枚あるだけですね。
それぞれの頂点に振られている数字は、頂点位置、ボーンの重み付け、どのボーンから影響を受けるかのインデックス(※1)、となっています。
※1 ... このインデックス、最終的にはボーンそのものではなく、ボーンから計算された「合成行列」へのインデックスとなります。
この合成行列は、今回のサンプルではグローバル領域に配列として用意してそこから取り出します。
詳しくは「合成行列」のところで説明します。
情報定義部分抜粋
今回はサンプルなので、手で情報を記述しています。
通常であればモデリングツールなどから出力されたデータをパースするなりしてデータを取り出すことになるでしょう。
その定義部分が以下です。
| プロパティ | 意味 |
|---|---|
| position | 頂点位置 |
| color | 頂点色 |
| normal | 頂点法線 |
| index | 頂点インデックス |
| boneIndices | 影響を受けるボーン(合成行列)のインデックス |
| weights | ボーンに対する重み付け |
// Planeの定義
var plane = {
position: [
2.0, 0.0, 0.0,
2.0, 1.0, 0.0,
3.0, 1.0, 0.0,
3.0, 0.0, 0.0,
2.0, 2.0, 0.0,
3.0, 2.0, 0.0,
2.0, 3.0, 0.0,
3.0, 3.0, 0.0,
2.0, 4.0, 0.0,
3.0, 4.0, 0.0,
2.0, 5.0, 0.0,
3.0, 5.0, 0.0,
],
color: [
1.0, 0.0, 0.0, 1.0,
0.0, 1.0, 0.0, 1.0,
0.0, 0.0, 1.0, 1.0,
0.0, 0.0, 0.0, 1.0,
1.0, 0.0, 0.0, 1.0,
0.0, 1.0, 0.0, 1.0,
0.0, 0.0, 1.0, 1.0,
0.0, 0.0, 0.0, 1.0,
1.0, 0.0, 0.0, 1.0,
0.0, 1.0, 0.0, 1.0,
0.0, 0.0, 1.0, 1.0,
0.0, 0.0, 0.0, 1.0,
],
normal: [
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
0.0, 0.0, 1.0,
],
index: [
0, 1, 2,
2, 3, 0,
1, 4, 5,
5, 2, 1,
4, 6, 7,
7, 5, 4,
6, 8, 9,
9, 7, 6,
8, 10, 11,
11, 9, 8,
],
boneIndices: [
0, 0, 0, 0,
1, 2, 0, 0,
0, 1, 0, 0,
0, 0, 0, 0,
1, 2, 0, 0,
1, 2, 0, 0,
2, 3, 0, 0,
2, 3, 0, 0,
3, 4, 0, 0,
3, 4, 0, 0,
4, 0, 0, 0,
4, 0, 0, 0,
],
weights: [
1.0, 0.0, 0.0,
0.5, 0.5, 0.0,
0.5, 0.5, 0.0,
1.0, 0.0, 0.0,
0.5, 0.5, 0.0,
0.5, 0.5, 0.0,
0.5, 0.5, 0.0,
0.5, 0.5, 0.0,
0.5, 0.5, 0.0,
0.5, 0.5, 0.0,
1.0, 0.0, 0.0,
1.0, 0.0, 0.0,
],
};
影響を受けるボーンインデックスは4つです。
が、これは記事を参考にしているため、なぜ4本なのかまだ詳しくは分かっていません・・。
(影響受けそうなのは2本だし、計算も2本だけだし)
たんに任意の数なのか、それ以外に理由があるのか。
見かけた理由としては、ボーンの数が多すぎるとuniform変数などの上限を超えてしまうから、というものでした。
(が、今回はそもそも頂点の移動をシェーダではなくJS側で行っているのであまり関係ありませんが)
影響を受けないボーンに関しては重みを「0」に
さて、本数は置いておいて、そもそも影響を受けるボーンがひとつなら定義もひとつでいいじゃないか、と思うかもしれません。
ですが、実際には数を統一しておくことで、不要なif文による分岐がいらなくなります。
こうした最適化がどうやら働いているようです。
(ただ、すでに書いたように今回はJSでやるのであまり意味はありません)
そしてweightsを0にしておけば、実質ボーンの影響は受けなくなる、というわけです。
4本目のボーンは1.0 - weight1 - weight2 - weight3で求める
さらによーく見てみると、weightsの定義は実は3つずつの数値のみです。
これはなんでかというと、ボーンの重み付けの中で4本目は1.0 - weight1 - weight2 - weight3として、1.0からの差分によって計算するからです。
おそらくですが、重み付けは合計で1.0を超えないようにするものなのでしょう。
こうすることで、必ず合計値が1を超えることがなくなります。
ボーンオフセット行列と初期姿勢行列
さて、続いてはボーンオフセット行列と初期姿勢行列です。
これらの行列がなにをしてくれるか。
ボーンオフセット行列 は、絶対座標で与えられた初期姿勢をなかったことにする行列です。
なかったことにする行列といえば逆行列ですね。
ボーンオフセット行列は逆行列
例えば、x: 2.5, y: 1.5の位置に移動する行列をなかったことにするには、x: -2.5, y: -1.5を計算してやればいいですね。
実際の行列はもっと複雑なことが多いので、こう単純には行きません。
そこで登場するのが逆行列、というわけです。
逆行列は、まさにこの「なかったこと」にしてくれる行列を生成する方法です。
ということを踏まえてボーンの初期化部分の処理を見てみると、以下のようになっています。
// 中略
init: function (position) {
this.matrix = mat4();
this.matrixBone = mat4();
this.matrixComb = mat4();
this.matrixInit = mat4.translate(mat4(), position);
this.matrixOffset = mat4.inverse(this.matrixInit);
this.children = [];
},
// 中略
この中でthis.matrixOffset = mat4.inverse(this.matrixInit);となっているのがその部分ですね。
初期化時に渡されるposition引数は絶対座標を想定しています。
なのでそのまま逆行列を求めて保持している、というわけですね。
余談
ちなみにここで登場しているmat4は自作のライブラリです。
GLSLと似たような操作ができることを目標としているものです。
なので、以下のような感じで使うことができます。
var v1 = vec3(0, 1, 0); // 3要素のベクトル
var v2 = vec2(0, 1);
var v3 = vec3(v2, 0); // vec2成分を流用してvec3を作る
var m1 = mat4(); // 引数なしで単位行列を作る
var m2 = mat4(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16); // 引数を与えて初期化
var m3 = mat4(m2); // 同じ値で複製
var result = mat4();
// OpenGLのように結果を得る行列を第3引数に指定する
mat4.multiply(m1, m2, result);
// 戻り値としても計算できる
// result = mat4.multiply(m1, m2);
オフセット行列の意味
なぜオフセット行列が必要なのか。それは、ボーンの意味を考えると見えてきます。
(Blenderなどのモデリングツールを使ったことがある人であれば想像しやすいと思います)
ボーンは、それ単体でも位置や姿勢を持っています。
モデリングツールでも視覚的に表示されるので分かると思います。
そして最初はモデルに対してボーンは紐付いていません。(ツール上で関連付けを行う必要がある)
なにが言いたいかと言うと、 ボーンの位置とモデルの位置には本来は関連性がない ということです。
ツール上で関連付けを行ったときに初めて関連性が生まれます。
そしてそのときのモデルの状態とボーンの状態を関連付け、それを 初期姿勢 として登録するわけです。
初期姿勢を決めておかないと、後々ボーンを動かしたときに関連付けられたモデルをどう動かせばいいか分からなくなってしまいますよね。
マリオネットに例えてみる
ふと思いついた例えをしてみます。
まず、マリオネットを想像してください。マリオネットは糸で結ばれ、離れた位置(上部)にある板を人間が操作することで、まるで生きているかのように動かしますよね。

↑こんな感じのものです。(こちらの記事から引用させて頂きました)
この糸が関連付けで、板がボーンの位置(※1)です。
板を少しだけ上に上げると、マリオネットも少しだけ上に上がります。
どれだけ上がるかは板をどれだけ上げたかによりますね。
これが「差分」です。
そして差分は、「初期位置からどれだけ動いたか」で求められますね。
このことからも分かるように、「初期姿勢」は大事な役割があるのです。
仮に、マリオネットが正常な状態ではなく、変な姿勢のまま糸と結び付けられてしまったら。
操作するための板を動かしても、思い通りには動きませんよね。
なので、初期姿勢として正しい位置を定義した上で関連付けを行うのです。
※1 ... 通常のモデリングツールではボーンはモデルに重なるようにするのが普通ですが、離れていても同様の動きをするのであくまで例えです。
親空間からの相対座標に変換
以下のヘルパーメソッドを見てください。
/**
* 各種ボーンを親空間の相対位置に変換
*/
Bone.calcRelativeMat = function (bone, parentOffsetMat) {
bone.children.forEach(function (childBone, idx) {
Bone.calcRelativeMat(childBone, bone.matrixOffset);
});
if (parentOffsetMat) {
mat4.multiply(bone.matrixInit, parentOffsteMat, bone.matrixInit);
}
};
やっていることを一言で言うと、「子ボーンの座標を親空間座標へ変換」です。
mat4.multiply(bone.matrixInit, parentOffsetMat, bone.matrixInit);の部分ですね。
掛ける順番に注意
行列に詳しい人であれば「おや?」と思うかもしれません。
なぜなら、OpenGL系の場合は親空間座標への変換の際は、その座標変換行列を 左側 に掛けるからです。
が、見てもらうと分かるように、parentOffsetMatは右側に来ています。
そもそもオフセット行列は 逆行列 です。
なので、通常通りに計算してしまうと「逆の移動」をしてしまうことになります。
だから反対から掛けている、というわけです。
初期姿勢行列を上書き
さらに見てもらうと分かりますが、matrixInit(初期姿勢用行列)自体を上書きしています。
つまり、初期姿勢は「親空間からの相対座標」である必要があるわけです。
ただ、絶対座標へ戻すための行列をオフセット行列としてすでに計算しているので、あとあと困ることはないのです。
差分姿勢
続いて差分姿勢です。
ちなみに今までの流れを見てみると、セットアップは以下のようになっています。
- ボーンオフセット行列
- 親空間座標での初期姿勢
- ボーン連結
これがなにを意味するかというと、ボーンの初期化が終わった、ということです。
ここからは ボーンをどう動かすか を計算するわけです。
(なので極端な話、ボーンをまったく動かさないのであれば、ここを飛ばして次の「合成行列」を生成しても問題なく動く、ということです)
差分を計算する
では実際にボーンを動かしてみましょう。
今回のサンプルでは単純に、すべてのボーンを少しだけ回転させるようにしています。
ボーンはいわゆるツリー構造になっているので、すべてのボーンを同じ角度だけ曲げていけば、自動的にカーブを描くようになっています。
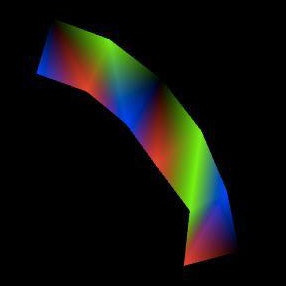
こんな感じになります
回転を計算
// countはフレームごとに増加していく
var s = Math.sin(count) / 5;
for (var i = 0; i < bones.length; i++) {
// `s`角度だけ全ボーンを回転させる
bones[i].rotate(s, axis);
}
// 合成行列を更新
Bone.updateBone(bones[0], global);
合成行列
さて、いよいよ仕上げです。
今までセットアップした行列たちを使って、最終的に使う合成行列を作ります。
合成行列は親ボーンの座標も必要になるので、ヘルパーメソッドを作り以下のようにしています。
/**
* 各種ボーンの合成行列を生成
*/
Bone.updateBone = function (bone, parentWorldMat) {
// 親の姿勢行列(ボーン行列)を左から自身の姿勢行列に掛ける
mat4.multiply(parentWorldMat, bone.matrixBone, bone.matrixBone);
// 自身のオフセット行列を右から掛けて合成行列を生成
mat4.multiply(bone.matrixBone, bone.matrixOffset, bone.matrixComb);
bone.children.forEach(function (childBone, idx) {
Bone.updateBone(childBone, bone.matrixBone);
});
};
親のボーン行列を、自身のボーン行列に掛けて、さらに自身のオフセット行列を掛けます。
(かける順番に注意)
なにをしているかというと、たんに 絶対座標に戻す ということをやっています。
親の座標変換行列を掛けることで、親の空間での座標系になります。
これを再帰的に繰り返せば、すべてのボーンがワールド空間上での絶対座標となります。
そして最後に、一番最初に計算しておいた オフセット行列 をかけることで、ボーンの初期位置からの差分位置にボーンが移動する、というわけです。
ボーン行列?
実は上記までで、ボーン行列を計算している箇所がありません。
これはなにをしているかというと、以下のようにボーンクラスのメソッドになっています。(例は回転)
// 中略
rotate: function (angle, axis) {
mat4.rotate(this.matrix, angle, axis, this.matrix);
this.updateMatrix();
},
// 中略
updateMatrix: function () {
mat4.multiply(this.matrixInit, this.matrix, this.matrixBone);
},
this.matrixは、ちょっと前に出てきた差分行列を表します。
これに、どういう移動や回転が行われたかを保持していきます。
そして最後のthis.updateMatrixメソッドで、親に対する相対行列となったmatrixInitとかけてやることで、親空間から見た位置がupdateされます。
合成行列の意味
合成行列は最終的に 頂点に影響を与える行列 です。
仮にボーンをなにも動かしていないことを考えると分かりやすいと思います。
(そしてルートボーンの初期位置は適当に(15, 8)とかと考えてください)
なにもしていないわけですから、普通はモデル(頂点)に変化はありませんね。
計算しても変化がない行列・・・つまり、合成行列を計算すると 単位行列 となります。
これがオフセット行列を求めておく意味です。
あとは、ボーンを動かしたいように平行移動、回転をさせていけば、単位行列に対して徐々に変化が蓄積されていきます。
結果、ボーンが動くことで、関連付けられたモデルが動く、というわけです。
頂点にボーンの影響を反映させる
さて、ボーンの計算は以上です。
ただ、ボーンの計算が終わっても、それを各種頂点に反映しないとまったく意味がありませんね。
ということで、計算されたボーンを頂点に適用してみましょう。
(ちなみにボーンの合成行列の適用は、今回はJS上で行っています。頂点をいじるのだから本来は頂点シェーダの仕事だと思いますが、知識不足なのとWebGLでの取り扱いかたが分からず、今回はJSで行っています)
まずはコードから。
var newPosition = [];
var newNormal = [];
for (var i = 0; i < 12; i++) {
var idxBase = i * 3;
var idx0 = idxBase + 0;
var idx1 = idxBase + 1;
var idx2 = idxBase + 2;
var comb1 = [
mat4(),
mat4(),
mat4(),
mat4()
];
var comb2 = mat4.zero;
for (var j = 0; j < 3; j++) {
var boneIdx = i * 4 + j;
var weightIdx = i * 3 + j;
mat4.multiplyScalar(combMatArr[plane.boneIndices[boneIdx]], plane.weights[weightIdx], comb1[j]);
}
var weight = 1.0 - (plane.weights[i * 3 + 0] +
plane.weights[i * 3 + 1] +
plane.weights[i * 3 + 2]);
mat4.multiplyScalar(combMatArr[plane.boneIndices[i * 4 + 3]], weight, comb1[3]);
for (var k = 0; k < 4; k++) {
mat4.add(comb2, comb1[k], comb2);
}
var pos = vec3(plane.position[idx0],
plane.position[idx1],
plane.position[idx2]);
vec3.applyMatrix4(pos, comb2, pos);
newPosition[idx0] = pos.x;
newPosition[idx1] = pos.y;
newPosition[idx2] = pos.z;
var nor = vec3(plane.normal[idx0],
plane.normal[idx1],
plane.normal[idx2]);
mat4.inverse(comb2, comb2);
vec3.applyMatrix4FromRight(nor, comb2, nor);
newNormal[idx0] = nor.x;
newNormal[idx1] = nor.y;
newNormal[idx2] = nor.z;
}
まず、なにをやっているか大まかな流れを書くと、
- 全頂点(サンプルでは12頂点)それぞれに計算を行う
- 頂点情報として割り当てられた値を元に、ボーンの合成行列の重み付けを計算する(
multiplyScalar) - 重み付けをした合成行列の合計を計算する(
add) - 得た行列を頂点、法線それぞれに掛ける
順番に見て行きましょう。
頂点ごとに計算を行う
今回のサンプルは簡単にするため、全部で12頂点です。
なのでforループで12回ループを回しています。
つまり頂点ごとに計算を行っているわけですね。
これがモデリングツールなどから得られたものなら、膨大な数の頂点があると思いますが基本は変わりません。
合成行列に重み付けをする
頂点定義のときに見たように、各頂点にはどのボーンからどれくらい影響をうけるかを定義していました。
それを元に、各種合成行列(つまりボーン)に重み付けをして計算をします。
抜粋すると以下の部分です。
for (var j = 0; j < 3; j++) {
var boneIdx = i * 4 + j;
var weightIdx = i * 3 + j;
mat4.multiplyScalar(combMatArr[plane.boneIndices[boneIdx]], plane.weights[weightIdx], comb1[j]);
}
ボーンをあらわす配列「combMatArr」
combMatArrは、少し前で計算したボーンの合成行列を格納した配列です。
今回はグローバルな領域においていますが、実際はボーンを管理するクラスなどで管理されるべきものでしょう。
ここでは単純に、該当のボーンの情報を取り出して重みを掛けている、と考えてください。
合成行列の合計を得る
重み付けをした合成行列が計算できたら、あとはそれを単純に足し合わせます。
重み付けは合計が1になるように計算されているので、設定された値によって適切にボーンの影響を受けるようになります。
(仮にひとつのボーンからのみ影響を受けるようにしたら、そのボーン以外の合成行列の値はすべて0になりますね)
最終結果を反映する
やっとゴールが見えてきました。
以上で、どの頂点にどういう影響を与えるべきかの計算が終わりました。
あとはこれを各種頂点情報に掛けてあげれば完成です。
が、少しだけ注意が必要です。
コードを見てみると、「頂点位置の計算」と「法線との計算で」若干違いがあります。
具体的には以下です。
var pos = vec3(plane.position[idx0],
plane.position[idx1],
plane.position[idx2]);
vec3.applyMatrix4(pos, comb2, pos);
newPosition[idx0] = pos.x;
newPosition[idx1] = pos.y;
newPosition[idx2] = pos.z;
var nor = vec3(plane.normal[idx0],
plane.normal[idx1],
plane.normal[idx2]);
mat4.inverse(comb2, comb2);
vec3.applyMatrix4FromRight(nor, comb2, nor);
newNormal[idx0] = nor.x;
newNormal[idx1] = nor.y;
newNormal[idx2] = nor.z;
頂点位置の場合は単純にvec3.applyMatrix4メソッドを使って、頂点位置に行列を適用しています。
一方、法線のほうは若干ややこしい計算をしています。
法線には「転置逆行列」を掛ける
計算は、得た行列の 逆行列 を掛け、さらに適用するメソッドも若干違うものが使われています。
これはなにをしているかというと、(自分もしっかり理解できていませんが)法線の場合は単純に座標変換行列を掛けると間違った答えになってしまいます。
ただ、転置逆行列 を掛けることで、その問題が解決できるようです。
(法線の変換の話という記事を参考にさせて頂きました)
これを実現しているのが上記のコード、というわけですね。
mat4.inverseは逆行列を得るメソッドです。
が、本来は転置行列にする必要がありますが、ここは少しずるをしています。
vec3.applyMatrix4FromRightメソッドは、ベクトルの「右側」から行列を適用するメソッドです。
(通常、OpenGL系では「左側」から行列を掛けます)
ですが、メソッド名の通り、行列を右から掛けることで転置行列を適用したことと同じ結果を得ている、というわけです。
あとは、ここで得た新しい頂点位置と法線を、新しい配列に入れ、その頂点バッファオブジェクト(VBO)を生成してそれをWebGLに送ってやればめでたくボーンの影響を受けた頂点が描かれる、というわけです。
だいぶ長い記事になってしまった・・( ;´Д`)
冒頭でも書きましたが、この記事のサンプルはjsdo.it(スキニングメッシュ(ボーン)で法線情報も扱う)に上がっているので見てみてください。