Cygames Engineers' BlogのゲームAI -基礎編- 『知識表現と影響マップ』を読んで色々と勉強になったので、使えるようにするべく実際に自分でもサンプルを作ってみようと思います。
今回は上記記事の中で「経路探索」に使われる「ダイクストラ法」をやってみました。
ちなみにこのアルゴリズムはカーナビの経路探索にも使われているらしいです。
今回の記事とサンプルの実装には、こちらの記事を参考にさせてもらいました。
デモ
今回のアルゴリズムの勉強のために簡単なデモを作ってみようと思って作り始めたら、途中から目的が変わってちょっとしたWebアプリを作るくらいの規模になりましたw(そのデモはこちら ※ ES6全開なので、Chromeじゃないと動きません;)
デモの総行数は3000くらいあるのに、メインであるはずのアルゴリズムの行数は100行程度です・・w
ちなみに見た目も凝ってみました(ㆆᴗㆆ)
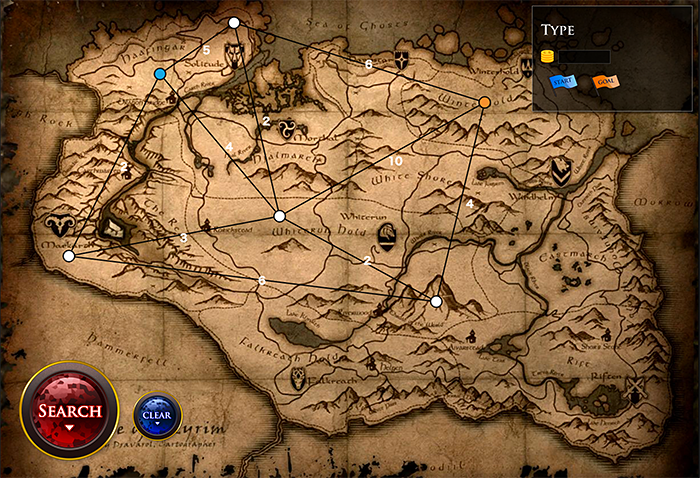
イメージとしてはゲームのいち画面で最短距離を見つける、みたいな感じのをイメージして作りました。
(全コードはGithubに上がっています)
操作方法
ノードの設定
ノード(丸いやつ)を選択すると スタートノード か ゴールノード かを選択することができます。
スタートにしたいノードを選択してスタートフラグ(青い旗)をクリックするとスタートノードにすることができます。
ゴールも同様です。(ゴールはオレンジの旗)
(ただ重複して設定しようとしても設定できません。デフォルトでスタートとゴールが設定されているので注意してください)
ノードを変更すると、ノード自体の色も変化します。
エッジの設定
ノードをつなぐラインが「エッジ」で、経路を表しています。
エッジを選択すると「コスト」が設定できます。コストはエッジの上に乗っている白い数字が表しています。
コストを大きくするとその経路が選択されづらくなります。(つまり一番コストが少ない経路を選択します)
(コストの設定は右上のインスペクタから行えます)
検索開始
スタートノードとゴールノードを設定したら、左下の「SEARCH」ボタンを押すと経路探索が開始され、最短経路がアニメーションで示されます。
余談
実はこのアニメーション部分の仕組み化に時間が取られました・・w
汎用的にアニメーションとアニメーションキューを制御できる仕組みを作ってます。
(実はアルゴリズムよりも汎用化のほうが収穫だったのは内緒)
ダイクストラ法実装概要
アルゴリズムを見ていく中で、どの解説もルートを遡って行ったり来たりしながら確定しているように説明されているので、つい「エッジの行き来を管理している」もんだとばかり思って考えていたんですが、実際はそうではなくて 総当り でした。
総当りで計算していくと、訪問済みとコストが徐々にアップデートされていき、すべてが「訪問済み」としてマークされると探索完了です。
上記の記事の一部を引用させてもらうと以下のイメージです。
ダイクストラ法はDP(動的計画法)的なアルゴリズムです。 つまり,「手近で明らかなことから順次確定していき,その確定した情報をもとにさらに遠くまで確定していく」方法で, DPと同じ精神を持っています。
プログラム的には総当りで各ノードをチェックし、確定しているか判断、確定していたら次のノードをチェックしコストをアップデート、というような流れで処理をしていきます。
図解
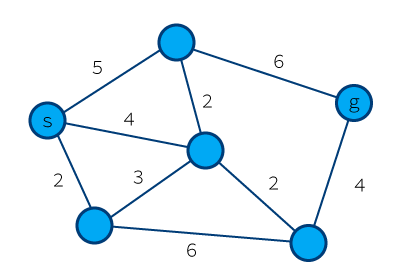
まず用語から。
上記の円を「ノード」と呼びます。そしてそのノードを結ぶ線が「エッジ」です。
円の中に「s」と書かれているのがスタートノード、「g」と書かれているのがゴールノードです。
スタートからゴールに行くのに最短の道はどれか、というのを解決するアルゴリズムです。
実際は各ノードのコストを確定していく作業
総当りでアップデートしていく、と前述しましたがものすごくざっくり処理を言うと、全ノードへのコストを決定する作業、と言えます。
なので全ノードのコストの計算が終わるまで処理は続きます。
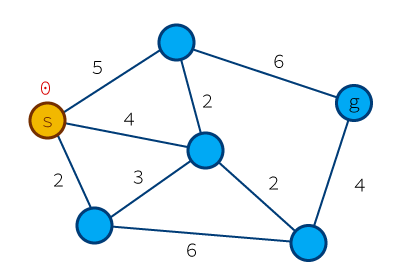
まず最初に、スタートノードのコストを 0 にして初期化します。
そこからスタートです。
実際の概要は参考にした記事を見たほうが分かりやすいと思うのでそちらをご覧ください。
ここでは、自分が最初に理解するときにハマった勘違いを説明し、上記記事の理解の助けとなることを目指して書きます。
確定したノードを除外し、各ノードへの最短コストを計算していく
さて、では実際にどういう処理をしているのでしょうか。
勘違いしていた部分は参考記事の以下の部分です。
次は距離4の中央のノードが(未確定ノードのうち)最短なので確定できます。 そして,中央のノードからは4つのエッジが伸びているので,それぞれ中央のノードを経由した(スタートノードからの)距離を計算します。
このあたりの説明で、エッジの状況を管理し、それを元にコストを計算しているのかと一瞬思ったのですが、そうではなく、あくまで全ノードは最後まで独立して考えます。
モデルデータとして主に保持しておくのは「訪問済みか」という点と「自分のコストはいくらか」という2点だけです。
そして探索のループの中で「訪問済み(= コスト確定済み)」のノードは無視され、まだ確定していないノードに対して暫定のコストを割り当てて行きます。
そして未確定ノードのうち、一番コストの少ないノードを見つけ、そこに接続しているエッジのコストを加算したコストを、接続先ノードに設定を試みます。
このとき、接続先のノードがすでに他のノードと接続されており、その計算中にすでにコストが設定されている場合は、そのコストと比較し、小さい場合に限り設定します。(最短経路の探索なので、それ以外の情報は必要ない)
今のコストとそれを更新するかだけを意識する
つまり、どこのノードからきてどこが最短経路なのかは探索が確定するまで分かりません。
必要なのは今自分が保持しているコストと、探索対象となった際にそのコストを採択するかだけに集中すればいいことになります。
(※ ちなみに「どこのノードからきたのか」は、コストをアップデートする度に接続元のノードを保持しておけば自動的に求まります)
コード
色々書きましたが、おそらくこれを見ている方の場合はコードを見てもらったほうが分かりやすいと思うので、まずはアルゴリズム部分のJSコードを載せます。
// ノード(経路の中継点)とそのノードを生成する
var nodes = createNodes();
// ノードの開始点のコストを0にする。(スタート地点は任意)
nodes[0].cost = 0;
// 経路が見つかるまでループする
while (true) {
// 現在処理中のノードを格納(これが見つからなければ終了)
var processNode = null;
// 全ノードに対して確認/アップデートを行う
for (var i = 0; i < nodes.length; i++) {
var node = nodes[i];
// 訪問済み or まだコストが未設定の場合はスキップ
// 結果として最初はスタートノードだけがコスト `0` になっているため、
// スタートノードが選択される。
if (node.done || node.cost < 0) {
continue;
}
// 処理中ノードがなければ現在のノードを保持して次へ
if (!processNode) {
processNode = node;
continue;
}
// 訪問済み(確定済み)でないノードのうち、一番小さいコストのノードを探す
if (node.cost < processNode.cost) {
processNode = node;
}
}
// 処理中のノードがなくなったら、つまりすべてチェックが終わったらループ終了
if (!processNode) {
break;
}
// 処理中ノードに「訪問済み」のフラグを設定する
// (未確定ノードのうち、一番コストが小さい場合はそこにいたるまでの経路が計算された結果なので「確定」できる
processNode.done = true;
// コストのアップデート
// 選択されたノード(processNode)の現在のコストと、
// 接続されているエッジのコストを足し、それを接続先のノードに設定されているコストと比較し、
// もしそれよりも小さければその値にアップデートする
for (var i = 0; i < processNode.edgesTo.length; i++) {
var node = processNode.edgesTo[i];
var cost = processNode.cost + processNode.edgesCost[i];
// コストが未設定 or コストの少ない経路がある場合はアップデート
var needsUpdate = (node.cost < 0) || (node.cost > cost);
if (needsUpdate) {
node.cost = cost;
node.previousNode = processNode;
}
}
}
// 上記で経路が検索済みとなる
// ここでは最後のノードをゴールとしているが
// 選択するノードを変更すればそのノードまでの最短経路が算出できる
var goalNode = nodes[5];
console.log('=====================');
var path = 'Goal -> ';
var currentNode = goalNode;
while(true) {
var nextNode = currentNode.previousNode;
if (!nextNode) {
path += ' Start';
break;
}
path += nextNode.id + ' -> ';
currentNode = nextNode;
}
console.log(path);
console.log('=====================');
以上がダイクストラ法の実装説明です。
以下はノードに対するモデルの説明です。
モデル
function Node(id) {
this.edgesTo = [];
this.edgesCost = [];
this.done = false;
this.cost = -1;
this.id = id;
this.previousNode = null;
}
Node.prototype.addNode = function (node, cost) {
this.edgesTo.push(node);
this.edgesCost.push(cost);
};
前述した通り、ノードモデルが持っているのは「確定済みか」のフラグと自身の「コスト」です。
加えて、そのノードから伸びているエッジの先につながっているノードの情報と、エッジ自体のコストを保持しています。
id は単純に識別用です。
previousNode は自身に接続している最短経路として選択されたノードを保持しています。
最短経路のコストだけを計算したい場合は必要ありません。
経路の作成
次は経路の作成です。
これは単純に、上記のノードモデルを使って相互に接続しているだけです。
モデルのコストなどは参考にした記事のものをそのまま使っています。
function createNodes() {
var node1 = new Node(1); // start
var node2 = new Node(2); // top
var node3 = new Node(3); // center
var node4 = new Node(4); // bottom-left
var node5 = new Node(5); // bottom-right
var node6 = new Node(6); // goal
node1.addNode(node2, 5);
node1.addNode(node3, 4);
node1.addNode(node4, 2);
node2.addNode(node1, 5);
node2.addNode(node6, 6);
node2.addNode(node3, 2);
node3.addNode(node2, 2);
node3.addNode(node1, 4);
node3.addNode(node4, 3);
node3.addNode(node5, 2);
node4.addNode(node1, 2);
node4.addNode(node3, 3);
node4.addNode(node5, 6);
node5.addNode(node4, 6);
node5.addNode(node3, 2);
node5.addNode(node6, 4);
node6.addNode(node2, 6);
node6.addNode(node5, 4);
return [
node1, node2, node3, node4, node5, node6
];
}
ソースコード
最後にソースコード全体を載せておきます。
スタートノードとしたいノードのコストを 0 にすることでスタートとすることができます。
(main 関数内の nodes の配列から指定する)
また、ゴールノードに関しては各ノードの経路検索が終わったタイミングで、ゴールノードを指定してそこから逆順に経路をたどっていくことで、ゴールノードからスタートノードまでの最短経路を表すことができます。
(なのでそれを反転すればスタートからゴールの最短経路となります)
/**
* ノード
*/
function Node(id) {
this.edgesTo = [];
this.edgesCost = [];
this.done = false;
this.cost = -1;
this.id = id;
this.previousNode = null;
}
Node.prototype.addNode = function (node, cost) {
this.edgesTo.push(node);
this.edgesCost.push(cost);
};
function createNodes() {
var node1 = new Node(1); // start
var node2 = new Node(2); // top
var node3 = new Node(3); // center
var node4 = new Node(4); // bottom-left
var node5 = new Node(5); // bottom-right
var node6 = new Node(6); // goal
node1.addNode(node2, 5);
node1.addNode(node3, 4);
node1.addNode(node4, 2);
node2.addNode(node1, 5);
node2.addNode(node6, 6);
node2.addNode(node3, 2);
node3.addNode(node2, 2);
node3.addNode(node1, 4);
node3.addNode(node4, 3);
node3.addNode(node5, 2);
node4.addNode(node1, 2);
node4.addNode(node3, 3);
node4.addNode(node5, 6);
node5.addNode(node4, 6);
node5.addNode(node3, 2);
node5.addNode(node6, 4);
node6.addNode(node2, 6);
node6.addNode(node5, 4);
return [
node1, node2, node3, node4, node5, node6
];
}
function main() {
var nodes = createNodes();
// start node is first node
nodes[0].cost = 0;
while (true) {
var processNode = null;
for (var i = 0; i < nodes.length; i++) {
var node = nodes[i];
// 訪問済み or まだコストが未設定
if (node.done || node.cost < 0) {
continue;
}
if (!processNode) {
processNode = node;
continue;
}
// 一番小さいコストのノードを探す
if (node.cost < processNode.cost) {
processNode = node;
}
}
if (!processNode) {
break;
}
processNode.done = true;
for (var i = 0; i < processNode.edgesTo.length; i++) {
var node = processNode.edgesTo[i];
var cost = processNode.cost + processNode.edgesCost[i];
// コストが未設定 or コストの少ない経路がある場合はアップデート
var needsUpdate = (node.cost < 0) || (node.cost > cost);
if (needsUpdate) {
node.cost = cost;
node.previousNode = processNode;
}
}
}
console.log('Has been done to search path.');
console.log(nodes);
var goalNode = nodes[5];
console.log('Shoten cost is ' + goalNode.cost);
console.log('Shoten path');
console.log('=====================');
var path = 'Goal -> ';
var currentNode = goalNode;
while(true) {
var nextNode = currentNode.previousNode;
if (!nextNode) {
path += ' Start';
break;
}
path += nextNode.id + ' -> ';
currentNode = nextNode;
}
console.log(path);
console.log('=====================');
}
// Start this program.
main();