OPTIMIZER 入門 ~線形回帰からAdamからEveまで

この記事について

機械学習で使われている optimizer について紹介するよ。

Introduction

まずは、みなさんも大好きな線形回帰を例に話をはじめましょう。普段は、何気なく機械学習のパッケージにデータを突っ込んで終わりということがほとんどではないでしょうか。パッケージの中で optimizer が蠢いていることも、ほぼ意識することはないかもしれません。しかし、彼らはそこにいるのです。

少し理論

さて、やや唐突ではありますが、目的変数を $y$、 説明変数を $X$、回帰係数を $w$ としましょう。線形回帰では、目的変数を説明変数の線形結合で近似したいと考えます。すなわち、

y \sim Xw \tag{1.1}

がなるべく"いい感じに"成り立つように係数 $w$ を決定することを目指します。ここで、$y$ と $w$ は縦ベクトル、$X$ は行列として扱っています。データのサンプル数を $N$ 、説明変数の数を $M$ とすれば、$y$ は $N$ 次元、$w$ は $M$次元、$X$ は $N\times M$ 次元です。なお、この記事では、記号の簡略化のため定数項は含めませんのでご注意ください。
"いい感じ"に $w$ を決定するためには損失関数を設定する必要があります。2乗誤差

L(w) := (y-Xw)^2 \tag{1.2}

が典型的なので採用します。損失関数 $L$ が最小となる $w$ の値を見つけるためには微分して"=0"となる点をみつければOKですので、微分してみましょう。

\frac{\partial L }{\partial w} = -2(X^Ty-X^TXw)=0 \tag{1.3}

より、

w=\big(X^TX\big)^{-1}X^Ty \tag{1.4}

が得られます。$X^T$ は $X$ の転置行列です。
これで万事解決。あとは (1.4) に機械的に $X$ と $y$ を放り込めば OK と思ったら大間違いです。そもそも、$X^TX$ の逆行列が存在しなければ (1.4) は意味をなしません。具体例で考えてみましょう。次のように設定してみます。

X=\begin{pmatrix}
1 & 1 & 1 \\
1 & 2 & 3
\end{pmatrix},\;
y=\begin{pmatrix}
0\\1
\end{pmatrix},\;
w=\begin{pmatrix}
a\\b\\c
\end{pmatrix} \tag{1.5}

この場合、$X^TX$を具体的に計算してみると

X^TX=
\begin{pmatrix}
1 & 1 \\
1 & 2 \\
1 & 3 \\
\end{pmatrix}
\begin{pmatrix}
1 & 1 & 1 \\
1 & 2 & 3
\end{pmatrix}
=
\begin{pmatrix}
2 & 3 & 4 \\
3 & 5 & 7 \\
4 & 7 & 10 
\end{pmatrix} \tag{1.6}

となっています。行列式も求めてみると

\text{det}\big(X^TX\big) = 0 \tag{1.7}

であり、逆行列は存在しないことが分かります。では、 (1.3) の解は存在しないのでしょうか。そんなことはありません。それどころか無数に存在します。(1.5) の設定もとでは、(1.1) は連立方程式

a+b+c=0, \;\; a+2b+3c=1 \tag{1.8}

と等価です。しかし、変数3つに対して方程式が2つなので解は一意には定まりません。実際に、$a$ と $b$ を $c$ について解いてしまえば、 $c$ をパラメータとした解の組

a=c-1, \;\; b=1-2c \tag{1.9}

が得られます。

パッケージを使ってみる

さて、ここで疑問がわきませんか。(1.5) の設定で機械学習のパッケージに放り込むと何が返ってくるのか、と。やってみましょう。python を使います。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from mpl_toolkits.mplot3d import Axes3D
sns.set_context('poster')

(1.5) に対応するデータを作ります。

X = np.array([[1, 1, 1],[1, 2, 3]])
y = np.array([[0],[1]])

scikit-learn に放り込んでみます。

from sklearn.linear_model import LinearRegression
np.random.seed(0)
model = LinearRegression(fit_intercept=False)
model.fit(X,y)

学習後の回帰係数を表示させてみます。

model.coef_

$a=-0.5$、$b=0$、$c=0.5$ という結果が返ってきました。確かに (1.8) を満たしているので、(1.9) の1つであることは確かです。しかし、$X^TX$ の逆行列が存在しないので (1.4) をもとに計算したのではないことは確かです。では、何が行われたのでしょうか。

Gradient Decent

線形回帰に限らず、少し一般的な話をしましょう。今、ある関数 $f(x)$ の最小値（or 最大値）を知りたいとします。引数の $x$ はベクトルとします。ある点 $x_0$ をひとつ固定し、$x_0$ の周りで微小な変動 $x_0$ → $x_0 + \Delta x$ を考えます。$\Delta x$ の1次の項まで残して展開すると

f(x_0+\Delta x)\simeq f(x_0)+\Delta x \cdot \frac{\partial f}{\partial x} (x_0) \tag{1.10}

と書けます。"$\cdot$"はベクトルの内積を表します。
さて、$\Delta x$ の方向をいろいろと取り換えた時に $f(x)$ の変化量が最も小さく（or 大きくなる）方向に進んでいけばうまい具合に最小値（or 最大値）を探索できそうです。そのためには、内積を最小(or 最大)化させればよいので

\Delta x \propto \mp \frac{\partial f}{\partial x} (x_0) \tag{1.11}

となればよい。つまり最小値を求めたい場合には、適当に初期位置を決めた後、time-step の添え字を $t$ として、

x_{t+1} = x_{t} -\eta \frac{\partial f}{\partial x}(x_t) \tag{1.12}

のように順次探索を繰り返せばよい訳です。$\eta$ は learning rate と呼ばれる定数で"小さな"正の値を手動で設定します。これが、Gradient Decent（勾配降下法）と呼ばれる手法で、最も基本的な optimizer です。
線形回帰の場合 (1.1) に、Gradient Decent の更新式を書き下してみると

\begin{align}
w_{t+1} &= w_t - \eta \frac{\partial L}{\partial w}(w_t) \\
        &= w_t - \eta \big[-2(X^Ty-X^TXw_t) \big] \tag{1.13}
\end{align}

となり、$X^TX$ の逆行列は必要ありません。また、(1.9) で無数の解が存在していたことは、探索の初期値に対応すると考えられます。

(1.13) をもとに線形回帰を実装してみましょう。

class LR_GradientDecent(object):

    def __init__(self, lr=0.01, n_iter=100, seed=0):
        self.lr = lr # learning rate
        self.n_iter = n_iter # number of iterations
        self.seed = seed # seed for initializing coefficients

    def fit(self, X, y):
        np.random.seed(self.seed)
        self.w = np.random.uniform(low=-1.0, high=1.0, size=(X.shape[1], 1)) # initializing coefficients
        self.loss_arr = np.array([])
        for _ in range(self.n_iter):
            self.loss_arr = np.append(self.loss_arr, (y-X.dot(self.w)).T.dot(y-X.dot(self.w)).flatten(), axis=0)
            dw = -2*(X.T.dot(y)-X.T.dot(X).dot(self.w)) # derivatives of the loss function
            self.w -= self.lr * dw # up-date coefficients

    def pred(self, X):
        return X.dot(self.w)

使ってみます。

model = LR_GradientDecent(n_iter=1000)
model.fit(X,y)

学習中の損失関数の値の変化を plot してみましょう。

plt.plot(model.loss_arr)
plt.xlabel('Number of Iterations')
plt.ylabel('Error')

回帰係数も見てみます。

model.w.flatten()

誤差の許容範囲をどうとるかにもよりますが、(1.9) は満たしています。
次に、初期値をいろいろ振って実験してみましょう。

coefs = []
err = []
for seed in range(200):
    model = LR_GradientDecent(n_iter=1000, seed=seed)
    model.fit(X, y)
    coefs.append(model.w.flatten())
    err.append(model.loss_arr[-1])
df_sol = pd.DataFrame(coefs)
df_sol.columns = ['a', 'b', 'c']
df_sol['error'] = err

df_sol

初期値の取り方によって、回帰係数の収束する値が全く異なることが見て取れます。いわゆる初期値依存性と言われるものです。ついでに、得られた回帰係数 $(a, b, c)$ を3次元マップに plot してみます。

fig = plt.figure()
ax = Axes3D(fig)
# solutions found by gradient decent
ax.plot(df_sol['a'], df_sol['b'], df_sol['c'], 'o', ms=4, mew=0.5)
# exact solutions
c = np.linspace(0, 1, 100)
a = np.array([i - 1 for i in c])
b = np.array([1-2*i for i in c])
ax.plot(a, b, c, color='yellow', ms=4, mew=0.5, alpha=0.4)
#ax.set_xlim(-1,0)
#ax.set_ylim(-1,1)
#ax.set_zlim(0,1)
#ax.set_xlabel('a')
#ax.set_ylabel('b')
#ax.set_zlabel('c')
ax.view_init(elev=30, azim=45)
plt.show()

上の図で、青丸が初期値を振りながら求めた回帰係数、薄い黄色線が厳密解 (1.9) を表しています。初期値を振ることで、青丸が黄色線上で散らばっている様子が分かるかと思います。

最後にもうひとつ。実は scikit-learn の LinearRegression では、Gradient Decent の更新式 (1.13) は使われていません。scikit-learn の内部事情には詳しくないのですが、ソースコード眺めたところ LSQR と言われる線形方程式を解くのに特化したアルゴリズムが使われている雰囲気がありました。このアルゴリズムも反復的な探索を繰り返しながら最小値を探っていくのですが、初期値の与え方が決まっているのか、seed をふっても得られる回帰係数は変化しませんでした。こう考えると、線形回帰のパッケージにデータを突っ込んで結果が返ってくると、一仕事終えた気になってますが、本当に意味のある答えが得られているのか、心がざわつきます。
なお、この記事では、モデルに特化したアルゴリズムというよりはもうちょっと一般的な視点に立って、Gradient Decent の後継者たちを紹介していきたいと思います。

Stochastic Gradient Decent (SGD)

さて、前章では Gradient Decent を紹介しましたが、これはバッチ処理でした。つまり、1-step ごとに全てのデータをまとめて処理しています。先の例ではデータのサンプル数が2つしかなかったので問題ありませんでしたが、データ量が大きくなると一括処理するのは難しくなってきます。また、オンラインでのデータストリームのように、全データをまとめて利用することが不可能な場合もあります。そこで、Gradient Decent を逐次的に処理する方法が必要になるわけで、これらは Stochastic Gradient Decent（確率的勾配降下法、以下SGD）と呼ばれます。
処理する塊の大きさは場合によりけりで、1-サンプル毎に処理を行う場合もあれば、ある程度のまとまり（ミニバッチ）での処理をすることもあります。一般に損失関数 $L$ は、データサンプル毎の和の形

L=\sum_{n=1}^NL_n \tag{2.1}

にかけるので、1-サンプル毎に処理する場合は (1.12) のアルゴリズムを各 $L_n$ に対して順次適応していきます。また、ミニバッチ処理の場合は、ミニバッチに含まれるサンプルについての和 $\sum_{n \in \text{mini-batch}}L_n$ に対して更新アルゴリズムを用います。
ところで、SGD には、Gradient Decent にはないご利益もあります。Gradient Decent では局所解にはまりこみ、抜け出せなくなる可能性が高いのですが、 SGD ではデータを取り換えて探索経路を揺さぶることで局所解から抜け出せる可能性が高くなります。ただし、1-サンプルごとの処理では、揺さぶり過ぎてしまい計算の収束性が悪くなってしまうため、ミニバッチ処理が好まれるようです。

以下の内容は、全データを一括処理すか、1-サンプルごとに処理するか、ミニバッチ処理するか、によらない一般的な話になりますので、損失関数も単に $L$ とだけ書くことにします。

SGD を継ぐもの

SGD は非常に単純なアルゴリズムですが、損失関数が複雑になればパフォーマンスは悪化します。そこで、SGD に改良を加えたアルゴリズムが様々に提案されてきました。ここからは、代表的な手法を紹介していきたいと思います。

Momentum SGD

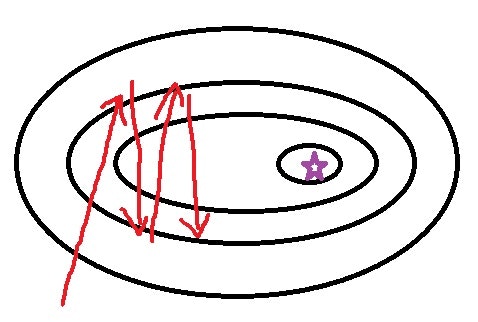
例えば、以下のような損失関数を考えてみて下さい。まずは左図をご覧ください。

SGD	Momentum SGD

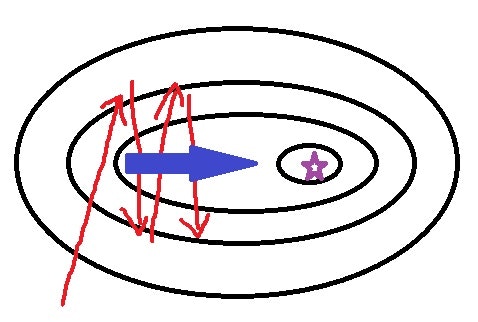黒い線が損失関数の等高線を表していて、紫の星印で最小値となっているとします。Gradient Decent の更新式 (1.12) に従えば、傾きが最小の方向に突っ込んでいくためジグザグ運動が始まり、なかなか目的の星印にたどり着けなくなっています。しかし、よく観察してみると、行ったり来たりしている部分の"平均"をとればジグザグ運動は相殺されて前方への推進力（右図の青矢印）が得られそうです。これが、Momentum SGD の発想です。式で書くと、

\begin{align}
& m_t = \gamma m_{t-1} + \eta \frac{\partial L}{\partial w}(w_t)　\tag{3.1}\\
& w_{t+1} = w_t - m_t \tag{3.2}
\end{align}

となります。$m_t$ の初期値は $m_0=0$ と設定します。(3.1) の $m$ が Momentum と呼ばれる項でジグザグ運動の相殺の役目をします。$g_t^{\eta}:=\eta \frac{\partial L}{\partial w}(w_t)$ と置いてみると、 (3.1) は

m_t=g_t^{\eta} + \gamma g_{t-1}^{\eta} + \gamma^2 g_{t-2}^{\eta} + \gamma^3 g_{t-3}^{\eta} + \cdots \tag{3.3}

と書き直せるので、減衰率 $\gamma$ で過去の garadient 情報を累積させていることが分かります。
(3.2) で $m_t$ を $g_t^\eta$ に置き換えると SGD に戻ります。$\gamma$ は$0.9$ 程度に設定されることが多いようです。

Nesterov accelerated gradient（NAG）

Nesterov accelerated gradient（NAG）は、Momentum SGD をちょっと改造したものです。先ほどの図では、紫の星印が目的地でした。ジグザグ運動を抑えたとしても、目的地できちんと止まってくれるのかが心配になってきます。到着直前に、自分の行先を予測してブレーキをかけてくれるとよさそうです。そこで、更新式を

\begin{align}
& m_t = \gamma m_{t-1} + \eta \frac{\partial L}{\partial w}(w_t - m_{t-1})　\tag{3.4}\\
& w_{t+1} = w_t - m_t \tag{3.5}
\end{align}

としてみます。(3.4) 右辺の gradient の評価が、いまの地点 $w_t$ ではなく移動予測地点 $w_t - m_{t-1}$ になっていることに注意してください。$m$ の time-step が $t-1$ なのは、$m_t$ を構成するのに $m_t$ 自身は使用できないためで、あくまで"予測"移動地点です。

AdaGrad

AdaGrad の基本は SGD ですが、学習パラメータ $w$ の各成分ごとに異なる learning rate を与え、あまり更新されていない成分には高い learning rate を割り振るように工夫します。以下、記号の簡略化のため

g^t_i:=\frac{\partial L}{\partial w_i}(w^t) \tag{3.6}

とおき、time-step の添え字 $t$ は右上に書くことにします。$i$ は ベクトル $w$ の成分を指定するインデックスです。
AdaGrad の更新アルゴリズムは以下で与えられ、

\begin{align}
& v^t_i = v^{t-1}_i + (g^t_i)^2 \tag{3.7} \\
& w^{t+1}_i = w^t_i - \frac{\eta}{\sqrt{v^t_i} + \epsilon} g^t_i　\tag{3.8}
\end{align}

$v$ の初期値は $v_i^0=0$ と設定します。$\eta$ は手動で与える定数で、やはり learning rate と呼ばれます。$\epsilon$ は $0$ による除算を防ぐために小さな値を設定します。また、$v^t_i$ は (3.7) より

v^t_i = (g^t_i)^2 + (g^{t-2}_i)^2 + (g^{t-3}_i)^2 + \cdots \tag{3.9}

とかけるので、更新があまり行われていない学習パラメータについては $v^t_i$ の値が小さくなり、実質的な learning rate $\eta/(\sqrt{v^t_i} + \epsilon)$ は大きくなります。$v^t_i$ についている square root "$\sqrt{\cdot}$" は、つけないとパフォーマンスが悪化するそうです。

RMSprop

AdaGrad では、(3.9) が示す通り、更新が繰り返されるほどに実質的な学習率が小さくなり、値の更新が止まってしまいます。これを防ぐのが RMSprop 目的です。過去の情報をすべて累積させていくのではなく、過去の累積と最新の情報を $\gamma : 1-\gamma$ の比率で案分しながら蓄積させていきます。すなわち、更新アルゴリズムは次のようになります。

\begin{align}
& v^t_i = \gamma v^{t-1}_i + (1-\gamma)(g^t_i)^2 \tag{3.10} \\
& w^{t+1}_i = w^t_i - \frac{\eta}{\sqrt{v^t_i}+\epsilon} g^t_i　\tag{3.11}
\end{align}

$v$ の初期値は $v_i^0=0$ と設定します。(3.10)を書き直すと

v^t_i=\gamma^t v^0_i + (1-\gamma)\sum_{l=1}^t \gamma^{t-l}(g^l_i)^2 \tag{3.12}

となることから、過去の情報は指数的に減衰しながら累積されていることが確認でき、移動指数平均といわれる一種の平均化法になっています。

AdaDelta

AdaDelta は RMSprop とは独立に提案されたようですが、機能的には RMSprop にもう一段階改造を加えたものになっています。ポイントは、学習パラメータが未探索領域に入った時に、探索距離を広げることです。更新アルゴリズムは、次のようになります。

\begin{align}
& v^t_i = \gamma v^{t-1}_i + (1-\gamma)(g^t_i)^2 \tag{3.13} \\
& s^t_i = \gamma s^{t-1}_i + (1-\gamma)(\Delta w^{t-1}_i)^2 \tag{3.14} \\
& \Delta w^t_i = -\frac{\sqrt{s^t_i + \epsilon}}{\sqrt{v^t_i + \epsilon}} g^t_i \tag{3.15} \\
& w^{t+1}_i = w^t_i + \Delta w^t_i　\tag{3.16}
\end{align}

初期値は $v_i^0=0$、$s_i^0=0$ と設定します。
(3.15) を見ると $\eta$ の代わりに $s^t$ が入っています。$w^t_i$ が大きく更新された場合、未探索の領域に突入しますが、(3.14) により $s^t_i$ も大きく更新されるため探索距離が広がるように工夫されています。
learning rate のパラメータを入れた式もたまに見かけます。

Adam

Adam は RMSprop に Momentum 法を組み合わせたような形をしています。更新アルゴリズムは以下のように与えられ、

\begin{align}
& m^t_i = \beta_1 m^{t-1}_i + (1-\beta_1)g^t_i \tag{3.17} \\
& v^t_i = \beta_2 v^{t-1}_i + (1-\beta_2)(g^t_i)^2 \tag{3.18} \\
& \hat{m}^t_i = \frac{m^t_i}{1-\beta_1^t} \tag{3.19} \\
& \hat{v}^t_i = \frac{v^t_i}{1-\beta_2^t} \tag{3.20} \\
& w^{t+1}_i = w^t_i - \frac{\eta}{\sqrt{\hat{v}^t_i}+\epsilon} \hat{m}^t_i　\tag{3.21}
\end{align}

初期値は $v_i^0=0$、$m_i^0=0$ と設定します。
(3.17) を

m^t_i=\beta_1^tm_0 + (1-\beta_1)\sum_{k=1}^t \beta_1^{t-k}g^k_i \tag{3.22}

と書き直してから初期値の $m_0=0$ を代入し、$g^k_i$ の order を $g^k_i \sim O[g]$ として両辺の order を比較してみると

O[m] \sim O[g] (1-\beta_1) \sum_{k=1}^t \beta_1^{t-k} = O[g](1-\beta_1^t) \tag{3.23}

となります。そもそも、$m^t$ は $g^t$ の"平均"であることを期待して導入したものでしたので、$1-\beta_1^t$ のずれが生じてしまうのは具合が悪そうです。特に、$\beta_1^t \sim 0$ のときは $O[m] \sim 0$ となってしまいます。そのための補正をかけているのが (3.19) です。(3.20) の補正も同様の理由によるものです。

Eve

Eve は 2016/11 ごろに、Adam の上位互換として提案された手法です。損失関数が複雑になってくると、特に deep learning などでは、局所的な最小値にはまり込むよりも寧ろ、鞍点や plateau と呼ばれる平坦な領域が学習を妨げている可能性が高いと指摘されています。しかし、SGD では損失関数の1階微分の情報だけを用いているため、どうしても対応しきれない面があります。そこで、Eve では、学習パラメータの更新に伴う損失関数の変動も直接利用します。変動量が小さいときには、鞍点・plateau にトラップされている可能性が高いと考え、学習パラメータの探索距離を伸ばします。その他の手順は Adam と同じで、更新アルゴリズムは以下のようになります。

\begin{align}
& m^t_i = \beta_1 m^{t-1}_i + (1-\beta_1)g^t_i \tag{3.24} \\
& v^t_i = \beta_2 v^{t-1}_i + (1-\beta_2)(g^t_i)^2 \tag{3.25} \\
& \hat{m}^t_i = \frac{m^t_i}{1-\beta_1^t} \tag{3.26} \\
& \hat{v}^t_i = \frac{v^t_i}{1-\beta_2^t} \tag{3.27} \\
& r^t = (\text{feed-back from the loss function}) \tag{3.28} \\
& d^t = \beta_3 d_{t-1} + (1-\beta_3) r^t \tag{3.29} \\
& w^{t+1}_i = w^t_i - \frac{\eta}{d^t \sqrt{\hat{v}^t_i}+\epsilon} \hat{m}^t_i　\tag{3.30}
\end{align}

(3.28) をどう構成すかがポイントです。(3.29) は過去分の feed-back と最新の feed-back の移動指数平均をとっていて、(3.30) の分母で追加されています。$d$ の初期値は $d^0=1$ と設定します。
さて、(3.28) の説明に移りましょう。まず、損失関数 $L(w)$ に対して $L^t:=L(w^t)$ を定義します。基本的には、$L$ の非負変化量 $\frac{L^{t}-L^{t-1}}{L^{t-1}}$ ($L^t > L^{t-1}$の場合)、$\frac{L^{t-1}-L^{t}}{L^{t}}$ ($L^{t-1} > L^t$の場合)をもって $r^t$ とするのですが、値が飛ぶなどして計算が安定しない可能性があるため、適当な定数の組 $0<k<K$ を設定して、$k < r^t < K$ となるように丸めてしまいます。しかし、論文によると、この単純な方法ではうまくいかなかったらしく、Eve では次のような手順を踏みます。
まず、$L^0=L(w^0)$ に対して $[\frac{L^0}{K+1},\frac{L^0}{k+1}]$（図中の②）、$[(k+1)L^0,(K+1)L^0]$（図中の⑤）を考えます。他にも $L^0$ を境にして図のように区間を切っておきます。

次に、$L^1=L(w^1)$ が得られたとします。$L^1$ に対して $L^0$ の周りに clip された $\hat{L}^1$ を、$L^1 \in $ ② or ⑤ ⇒ $\hat{L^1}=L^1$、$L^1 \in $ ① ⇒ $\hat{L^1}=\frac{L^0}{K+1}$、$L^1 \in $ ③ ⇒ $\hat{L^1}=\frac{L^0}{k+1}$、$L^1 \in $ ④ ⇒ $\hat{L^1}=(k+1)L^0$、$L^1 \in $ ⑥ ⇒ $\hat{L^1}=(K+1)L^0$ と定義します。この $\hat{L}^1$ を用いて $r^1$ $=$ $\frac{\hat{L}^{1}-L^{0}}{L^{0}}$ ($\hat{L}^1 > L^0$の場合)、$\frac{L^{0}-\hat{L}^{1}}{\hat{L^{1}}}$ ($L^{0} > \hat{L}^1$の場合) とします。すると、$k<r^1<K$ が必ず満たされます。続いて、$L^2=L(w^2)$ が得られた後は、前ステップでの $L^0$ を $\hat{L}^1$ に、$L^1$ を $L^2$ に代えて同じ要領で $\hat{L}^2$ を求め、$r^2$ を構成します。以下、この繰り返しです。要は、損失関数の値が学習の途中ステップでたまたま大きくなってしまった時の悪影響を排除したいのだと思います。実装する際は、上の説明より論文中の pesudo code をみた方が早いです。

２次なるものたち・・・

Gradient Decent は1階微分までを用いる方法でしたが、勿論2階微分を用いる方法もあります。代表的なものは Newton 法です。(1.10) において、$f$ → $\partial f / \partial x$ と置き換えると

\frac{\partial f}{\partial x}(x_0+\Delta x)\simeq \frac{\partial f}{\partial x}(x_0)+ \frac{\partial f}{\partial x \partial x}(x_0) \Delta x \tag{4.1}

となります。ここで、$\partial f / \partial x \partial x$ は、2階微分からつくられる行列（Hessian）です。今知りたいのは、$\partial f / \partial x=0$ となる点なので、(4.1) の右辺を "=0" と置いて

\Delta x = - \Big[\frac{\partial f}{\partial x \partial x}(x_0)\Big]^{-1}\frac{\partial f}{\partial x}(x_0) \tag{4.2}

を得ます。この式をもとに更新アルゴリズムを

x_{t+1} = x_t -\Big[\frac{\partial f}{\partial x \partial x}(x_t)\Big]^{-1}\frac{\partial f}{\partial x}(x_t) \tag{4.3}

で定めます。これが Newton 法と呼ばれるもので Gradient Decent の式 (1.12) と比較すると learning rate $\eta$ が Hessian の逆行列に置き換わっていることがわかります。
ところで、Hessian の幾何学的な意味は"曲率"です。すなわち、平坦な領域が広がるところでは"=0"、等高線が込み合っている領域では大きな値を持ちます。(4.3) では、Hessian の逆行列をとっているため、平坦な領域での探索距離を大きくする効果があると分かります。ただし、鞍点にはトラップされてしまうことに注意しておきましょう。鞍点では、Hessian の固有値が正になる方向と負になる方向が存在し、前者に沿って動くと鞍点は最小値、後者に沿っては最大値と見えます。固有値正の方向に対しては、Gradient Decent の場合と同じく鞍点に引っ張られます。一方で、固有値負の方向に対しては、(1.12) 式の微分項の係数が反転した形になってしまうため、最小値ではなく最大値をもとめるアルゴリズムに帰着し、この場合も鞍点に引き込まれます。この点を改良した手法も幾つか提案されてはいますが、大規模なモデルで Hessian を求めること自体が大変なので機械学習ではあまりつかわれていないと思います。Hessian をどのように計算/近似するかについても、各種の技法が開発されています。

参考ページなど

・勾配降下法
勾配降下法の最適化アルゴリズムを概観する
Theano 実装例 : ニューラルネットで最適化アルゴリズムを色々試してみる
・LSQR
原論文
共役勾配法
・Eve
論文 : Improving Stochastic Gradient Descent with Feedback