この記事について
ランダムウォークを例題にカルマンフィルターを実装してみるよ。
カルマンフィルターとは
ノイズという名のペルソナを引きはがし、真の姿を推定するテクニックです。
理論的なこと
典型的な設定として、下のようなシステムを考えてみましょう。
\begin{align}
x_{t+1} &= F_t x_t + G_t w_t \tag{1.1}\\
y_t &= H_t x_t + v_t \tag{1.2}\\
\end{align}
$x_t$はシステムの内部状態を表し、$y_t$はその観測値です。内部状態$x_t$は$(1.1)$に従い時間発展していきます。一方で、観測値$y_t$は$(1.2)$に従って、ノイズが乗った状態で掃き出されます。観測値$y_t$から、直接観測できない内部状態$x_t$を推測することが目的です。
設定を簡単にするため、$w_t$ と$v_t$はそれぞれ独立なガウス分布に従い、同時刻でのみ自己相関を持つとします。$w_t$と$v_t$の独立性とベイズ定理を用いると
\begin{align}
p(x_t|Y^t) &= \frac{p(y_t|x_t)p(x_t|Y^{t-1})}{p(y_t|Y^{t-1})} \tag{2.1}\\
p(x_{t+1}|Y^t) &= \int p(x_{t+1}|x_t)p(x_t|Y^t)dx_t \tag{2.2}
\end{align}
という関係式が得られます。ここで、$Y^t$は時刻$t$までの$y_t$の値、つまり
Y^t=\left\{y_1, y_2, ..., y_t\right\}
を表すものとします。
さて、$(2.1)$からは、時刻$t$までの観測値$Y^t$が分かった状態での、$x_t$の推定値$\hat{x}_{t|t}$が得られます。しかし、$(2.1)$の右辺を見ると$p(x_t|Y^{t-1})$が入っています。そのため、$\hat{x}_{t|t}$を得るには、時刻$t-1$までの観測値$Y^{t-1}$が分かった状態での$x_t$の推定値$\hat{x}_{t|t-1}$を知っておく必要があります。この$\hat{x}_{t|t-1}$は、$(2.2)$より得られますが、$(2.2)$の右辺を見ると、$\hat{x}_{t|t-1}$を得るには、さらに$\hat{x}_{t-1|t-1}$が必要となってくることが見て取れます。
以上より、$\hat{x}_{t|t-1}$と$\hat{x}_{t|t}$を交互に計算しながら$x_t$の推定を行うという流れになることが納得できるはずです。
一方で、終端時刻までの観測値が得られているならば
p(x_t|Y^N) = \int \frac{p(x_{t+1}|x_t)p(x_t|Y^t)p(x_{t+1}|Y^N)}{p(x_{t+1}|Y^t)}dx_{t+1} \tag{2.3}
という式も導けます。ここで、$N$は終端時刻とします。$(2.3)$より、全ての観測値$Y^N$が得られた状態での$x_t$の推定値$\hat{x}_{t|N}$が得られます。ただし、右辺の分子/第3項を見ると、$\hat{x}_{t+1|N}$をあらかじめ求めておく必要があるとわかります。よって、$\hat{x}_{t|N}$を求める過程は、時間の逆順に$t=N$から$t=1$に向かって進みます。また、$(2.3)$の右辺の分子/第2項からは、$\hat{x}_{t|t}$も求めておかなければならないと分かりますので、時間について順方向の推定の後に逆方向の推定を行います。この逆方向に進む過程は、スムージングと呼ばれています。
ランダムウォークで実験
ランダムウォーク
簡単な例題として、ランダムウォークの場合を考えてみましょう。$(1.1)$、$(1.2)$の式は
\begin{align}
x_{t+1} &= x_t + w_t \tag{3.1}\\
y_t &= x_t + v_t \tag{3.2}
\end{align}
となります。ただし、$w_t$と$v_t$はそれぞれ独立なガウス分布に従うものとし、同時刻でのみ自己相関を持つとします。
$(3.1)$がランダムウォークの真の動きを表し、$(3.2)$でノイズが加わり観測値が得られていると考えるといいでしょう。観測値の$y_t$しかわかっていないけど、ノイズを除去してもとの$x_t$を推測したいという状況です。
ついでなので、pythonでランダムウォークを作ってみましょう。使うパッケージは下の3つで十分です。
import numpy as npimport numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context('poster')
上の式を実装していきます。まずは、$(3.1)$のランダムウォークを作り、その後で$(3.2)$のようにノイズをのせます。
def random_walker(start_position=0, mean=0, deviation=1, n_steps=99, seed=None):
if seed is not None:
np.random.seed(seed=seed)
move = np.random.normal(loc=mean, scale=deviation, size=n_steps)
position = np.insert(move, 0, start_position)
position = np.cumsum(position)
return position
def add_noise(position, mean=0, deviation=10, seed=None):
if seed is not None:
np.random.seed(seed=seed)
n_observation = len(position)
noise = np.random.normal(loc=mean, scale=deviation, size=n_observation)
observation = position + noise
return observation
実際にノイズがのったランダムウォークを生成してみましょう。スタート位置は0とします。また、実際のランダムウォークの分散($w_t$の分散)を1、ノイズの分散($v_t$の分散)を10とします。平均はともに0とします。タイムステップは1~100としておきます。
true_position = random_walker(start_position=0, mean=0, deviation=1, n_steps=99, seed=0)
observed_position = add_noise(true_position, mean=0, deviation=10, seed=0)
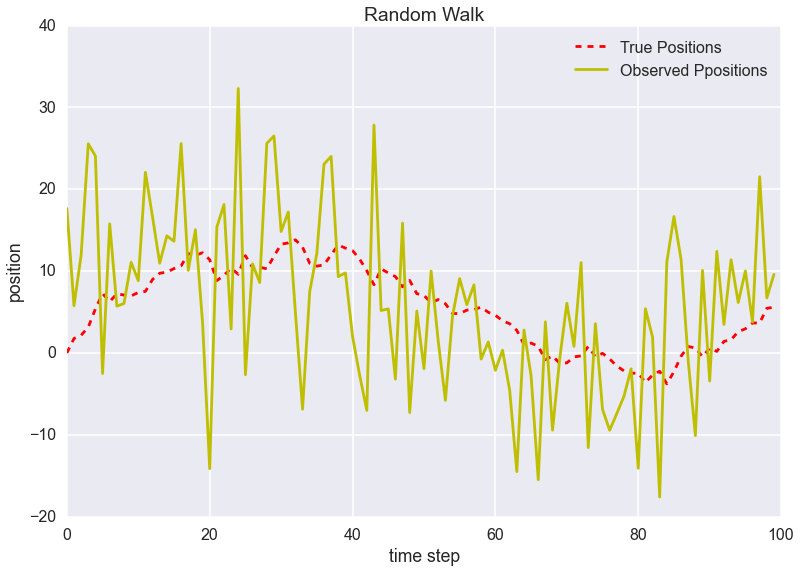
グラフにしてみましょう。
plt.plot(true_position, 'r--', label='True Positions')
plt.plot(observed_position, 'y', label='Observed Ppositions')
plt.title('Random Walk')
plt.xlabel('time step')
plt.ylabel('position')
plt.legend(loc='best')
見事なランダムウォークですね。
True Positionsがランダムウォークの真の値$x_t$、Observed Positionsがノイズののった観測値$y_t$です。
観測値が汚いですね。
カルマンフィルター
このランダムウォークモデルに合わせて、カルマンフィルターの式を書き下してみましょう。$w_t$は平均0、分散$q$のガウス分布に、$v_t$は平均0、分散$r$のガウス分布に従うとします。
導出は省きますが、時間の順方向に$\hat{x}_{t|t-1}$、$\hat{x}_{t|t}$を求めていく式は、
\begin{align}
&\hat{x}_{t/t} = \hat{x}_{t/t-1} + K_t(y_t - \hat{x}_{t/t-1}) \\
&\hat{x}_{t+1/t} = \hat{x}_{t/t} \\
&K_t = \frac{P_{t/t-1}}{P_{t/t-1} + r} \\
&P_{t/t} = \frac{r P_{t/t-1}}{P_{t/t-1} + r} \\
&P_{t+1/t} = P_{t/t} + q \\
\end{align}
時間の逆順に$\hat{x}_{t|N}$を求めていく式は、
\begin{align}
&\hat{x}_{t/N} = \hat{x}_{t/t} + C_t(\hat{x}_{t+1/N} - \hat{x}_{t+1/t}) \\
&C_t = \frac{P_{t/t}}{P_{t/t} + q} \\
&P_{t/N} = P_{t/t} + C^2_t(P_{t+1/N} - P_{t+1/N})
\end{align}
となります。これを実装してみましょう。
class Simple_Kalman:
def __init__(self, observation, start_position, start_deviation, deviation_true, deviation_noise):
self.obs = observation
self.n_obs = len(observation)
self.start_pos = start_position
self.start_dev = start_deviation
self.dev_q = deviation_true
self.dev_r = deviation_noise
self._fit()
def _forward(self):
self.x_prev_ = [self.start_pos]
self.P_prev_ = [self.start_dev]
self.K_ = [self.P_prev_[0] / (self.P_prev_[0] + self.dev_r)]
self.P_ = [self.dev_r * self.P_prev_[0] / (self.P_prev_[0] + self.dev_r)]
self.x_ = [self.x_prev_[0] + self.K_[0] * (self.obs[0] - self.x_prev_[0])]
for t in range(1, self.n_obs):
self.x_prev_.append(self.x_[t-1])
self.P_prev_.append(self.P_[t-1] + self.dev_q)
self.K_.append(self.P_prev_[t] / (self.P_prev_[t] + self.dev_r))
self.x_.append(self.x_prev_[t] + self.K_[t] * (self.obs[t] - self.x_prev_[t]))
self.P_.append(self.dev_r * self.P_prev_[t] / (self.P_prev_[t] + self.dev_r))
def _backward(self):
self.x_all_ = [self.x_[-1]]
self.P_all_ = [self.P_[-1]]
self.C_ = [self.P_[-1] / (self.P_[-1] + self.dev_q)]
for t in range(2, self.n_obs + 1):
self.C_.append(self.P_[-t] / (self.P_[-t] + self.dev_q))
self.x_all_.append(self.x_[-t] + self.C_[-1] * (self.x_all_[-1] - self.x_prev_[-t+1]))
self.P_all_.append(self.P_[-t] + (self.C_[-1]**2) * (self.P_all_[-1] - self.P_prev_[-t+1]))
self.C_.reverse()
self.x_all_.reverse()
self.P_all_.reverse()
def _fit(self):
self._forward()
self._backward()
それでは、先ほどのランダムウォークに適用してみましょう。実際は、ランダムウォークやノイズの分散の真の値はわからない場合が普通なので推定する必要があります。とりあえず、ここでは真の値を使ってしまいましょう。
kf = Simple_Kalman(observed_position, start_position=0, start_deviation=1, deviation_true=1, deviation_noise=10)
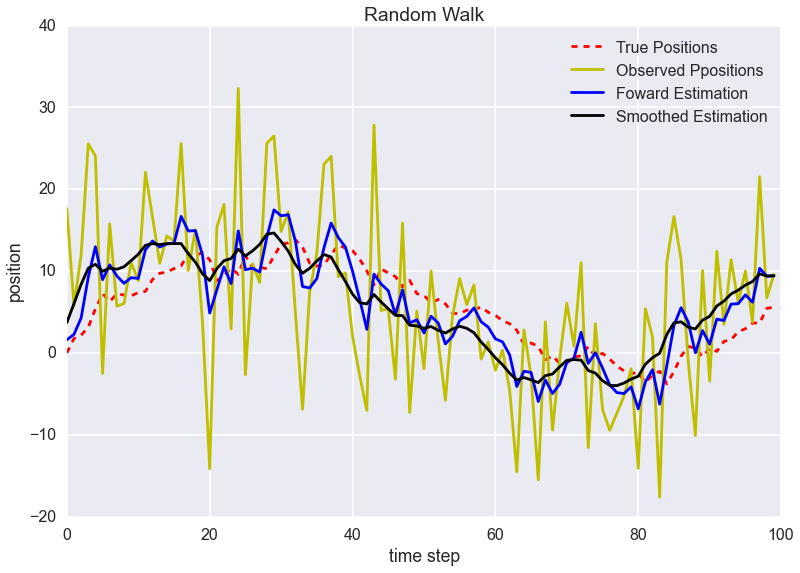
グラフにしてみます。
plt.plot(true_position, 'r--', label='True Positions')
plt.plot(observed_position, 'y', label='Observed Ppositions')
plt.plot(kf.x_, 'blue' ,label='Foward Estimation')
plt.plot(kf.x_all_, 'black', label='Smoothed Estimation')
plt.title('Random Walk')
plt.xlabel('time step')
plt.ylabel('position')
plt.legend(loc='best')
Forward Estimationが$\hat{x}_{t|t}$を、Smoothed Estimationが$\hat{x}_{t|N}$を表しています。
きれいになりましたね。
参考文献
非線形カルマンフィルタ
朝倉書店、片山徹
数式はこの本を参考にしています。
ノイズを除去した見事な表紙ですね。