技術動向についていくことは多くの労力を必要とする。次々に新しい論文が発表されるためだ。
一方で最新論文さえも長年の地道な積み重ねの上にあることを、その引用文献から気付かされる。
ディープラーニングブームの流れも変わるのだろうか?
勉強のため、2017年2月28日付けでarXivに投稿されたZhi-Hua Zhou, Ji Feng「Deep Forest: Towards An Alternative to Deep Neural Networks」を翻訳した。
訳には誤りがないよう注意を払いましたが、完全であることを保証できないため、実装等の際には元論文を参照願います。
原文:
Deep Forest: Towards An Alternative to Deep Neural Networks
https://arxiv.org/abs/1702.08835
https://arxiv.org/pdf/1702.08835.pdf
Deep Forest :Deep Neural Networkの代替へ向けて
Zhi-Hua Zhou および Ji Feng
National Key Laboratory for Novel Software Technology
Nanjing University, Nanjing 210023, China
概要
本論文では,ディープニューラルネットワークと高度に互角(highly competitive)の性能を持つ決定木アンサンブル手法であるgcForestを提案する.ハイパーパラメータチューニングに多大な労力を必要とするディープニューラルネットワークとは対照的に,gcForestは訓練が非常に容易である.
実際,gcForestは異なるドメインの異なるデータに適用された場合でも,ほとんど同じハイパーパラメータ設定で優れた性能を達成する.gcForestの訓練過程は効率的でスケーラブルである.実験においてPCでの実行時間は,GPU設備有りでのディープニューラルネットワークの実行時間と互角であり,gcForestが本来的(naturally)に並列実装に適しているためその効率性の利点はより明らかとなるだろう.さらに,大規模な訓練データを必要とするディープニューラルネットワークとは対照的に,gcForestは小規模データしかない場合でも良く動作する.その上,決定木ベースのアプローチであるため,gcForestはディープニューラルネットワークよりも論理的な解析が容易となる.
1 導入
近年,ディープニューラルネットワークが多くの応用において多大な成功を収めているが,とりわけ視覚と言語情報を含むタスクにおいて[Krizhenvskyら., 2012; Hintonら., 2012],ディープラーニングの熱波へとつながっている[Goodfellow ら., 2016].
ディープニューラルネットワークは強力だが,明らかな欠点がある.まず,その訓練には通常大量の訓練データが要求されることが知られているが,このためにディープニューラルネットワークを小規模データのタスクに適用することができない.ビッグデータの時代であっても,多くの現実のタスクはラベル付けコストのために未だ十分な量のラベル付きデータが不足しており,そのようなタスクでのディープニューラルネットワークの性能を低いものにしている.第二に,ディープニューラルネットワークは非常に複雑なモデルであり,訓練プロセスには通常強力な計算設備が必要とされるが,これは大企業に所属しない個人が完全にその学習能力を利用することを妨げる.更に重要なことに,ディープニューラルネットワークはハイパーパラメータが多すぎ,また,その学習パフォーマンスはそれらの慎重なチューニングに非常に依存してしまう.例えば,何人かの著者が皆,畳み込みニューラルネットワークを使用しているが[LeCunら., 1998; Krizhenvskyら., 2012; Simonyan および Zisserman, 2014],畳み込み層の構造のような多くの異なる選択肢が存在するために彼らは実際には異なる構造の学習モデルを使用している.この事実はディープニューラルネットワークの訓練を,科学/工学というよりもアートのように,非常にトリッキーにするだけでなく,ほとんど無限の設定の組み合わせと,干渉する要素が多すぎるためにディープニューラルネットワークの論理的な分析を非常に困難にしている.
ディープニューラルネットワークにとって*表現学習(representation learning)*の能力が重要であることは広く認知されている.また,巨大な訓練データを利用するためには,学習モデルの容量が大きくあるべきだということは注意すべきである;このことはサポートベクトルマシンのような通常の学習モデルよりもディープニューラルネットワークが非常に複雑である理由を部分的に説明している.私達はこれらの資産を,何か別の適した形の学習モデルへ付与できると考えており,前述の欠点がより少ない形で,ディープニューラルネットワークと互角の性能を達成することに成功した.
本論文では,最先端の決定木アンサンブル手法であるgcForest(multi-Grained Cascade forest)を提案する.この手法はgcForestに表現学習を可能にするカスケード構造を持つディープフォレストアンサンブルを生成する.入力が高次元の場合には,その表現学習の能力はmulti-grained scanningによって更に推進されるが,これは潜在的に,gcForestに文脈または構造を意識させることを可能にする.カスケード階層の数は適応的に決定されるが,その結果モデルの複雑さが自動的に設定され,gcForestが少量データに対してさえ優れた性能を発揮することを可能にする.gcForestのハイパーパラメータがディープニューラルネットワークよりも大幅に少ないことは特筆に値する;さらに良いことにはその性能がハイパーパラメータの設定に対して非常に頑健であり,そのために多くのケースで異なる領域の異なるデータをまたいでも,デフォルト設定のままで優れた性能を発揮することができる.このことはgcForestの訓練を便利にするだけではなく,本論文が対象とする範囲からは外れるが,ディープニューラルネットワークに比べて論理的な解析を簡単にする(言うまでもなく,木学習器は通常ニューラルネットワークよりも解析が簡単である).私達の実験では,PCで実行するgcForestの訓練時間のコストはGPU設備付きで実行するディープニューラルネットワークと互角である一方,gcForestはディープニューラルネットワークに比べて高度に互角またはより優れた性能さえ達成した.効率性においての利点はgcForestが本来的に並行実装に適している(naturally apt to parallel implementation)ので更に明確にできることは特筆に値する.
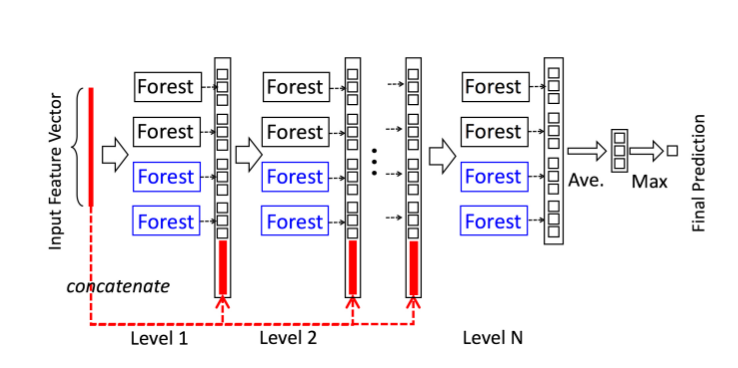
図1:カスケードフォレスト構造の説明.カスケードの各階層は2つのランダムフォレスト(青色)と2つの完全ランダム決定木フォレスト(黒)を含む.予測すべき3つのクラスがあるものとする;それ故,各フォレストは3次元クラスベクトルを出力し,その後それらは元入力の再表現のために結合される.
私達は複雑な学習問題に挑戦するためには,学習モデルはより深くならざるを得ないものと考えている.現在のディープモデルは,しかし,いつもニューラルネットワークである.本論文はディープフォレストの構築方法を説明するが,それは多くのタスクにおいてディープニューラルネットワークの代替へ向かう扉を開くことになるかもしれない.
次のセクションではgcForestを導入し実験の報告を行う.続けて関連研究と結論を述べる.
2 提案手法
このセクションでは最初にカスケードフォレスト構造を導入し,その後multi-grained scanningを,続けて全体のアーキテクチャとハイパーパラメータに関する注意を述べる.
2.1 カスケードフォレスト(Cascade Forest)
ディープニューラルネットワークにおける表現学習はほとんどが生の特徴量の層ごとの処理に依存している.この認識に基づいて,gcForestは多段構造(cascade structure)を採用しているが,図1に示すように,段の各レベルはその前段で処理された特徴情報を受け取り,自身の処理結果を後段に出力する.
それぞれの段は決定木フォレストのアンサンブルである.つまり,アンサンブルのアンサンブルである.ここで,多様性を高めるために異なるタイプのフォレストを含めるが,多様性はアンサンブルの構築にとって重要であることはよく知られている[Zhou, 2012].
簡単のために,今回の実装では2つの完全ランダム決定木フォレスト(complete-random tree forest)と2つのランダムフォレストを使用した[Breiman, 2001].
それぞれの完全ランダム決定木フォレストは1,000個の完全ランダム決定木(complete-random trees)[Liu ら., 2008]を含んでいるが,それらは木の各ノードでの分割のためにランダムに特徴を選択することで生成され,各葉ノードが同じクラスのインスタンスだけとなるか,またはインスタンス数が10以下となるまで成長を続ける.同様に,各ランダムフォレストは1,000個の木を含むが,それは候補として√d個の特徴をランダムに選択して(dは入力特徴数),その中で最もジニ値が良い一つを分割に使用することで作成される.各フォレストの木の数はハイパーパラメータであり,2.3節で議論する.
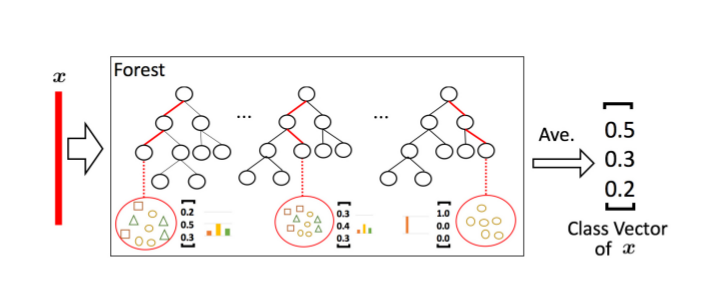
図2:クラスベクトル生成の説明.葉ノード中の異なるマークは異なるクラスを示す.
インスタンスを受け取ると(Given an instance),各フォレストは関心のあるインスタンス(concerned instance)が分類されてくる葉ノードにおいて異なるクラスの訓練例のパーセンテージを数えることでクラス分布の推定を生成する.それから同じフォレストの全ての木について平均を取る.これを図2に示す.インスタンスが葉までやってくるパスは赤のハイライトで示している.
推定されたクラス分布はクラスベクトルを形成するが,これはその後次の段のカスケードへ入力するために元の特徴ベクトルと結合される.例えば3つのクラスがあるとして,4つのフォレストそれぞれが3次元のクラスベクトルを生成する;したがって,次段のカスケードは12=3×4の拡張された特徴を受け取ることになる.
過学習のリスクを減らすため,各フォレストで作るクラスベクトルはk-foldクロスバリデーションで生成する.より詳細には,それぞれのインスタンスはk-1回訓練データとして使われ,k-1クラスのベクトルとなるが,その後,次段のカスケードのために拡張された特徴として最後のクラスベクトルを作るために平均化される.新しい段を拡張した後は,カスケード全体の性能はバリデーションセットで推定され,その訓練手続きは大きな性能向上がなくなったときに消去される;故に,カスケードの段数は自動的に決定される.モデルの複雑さが固定される多くのディープニューラルネットワークとは対照的にgcForestはそのモデルの複雑さを,適切なときに訓練を終了することで適応的に決定する;このことは,gcForestを大規模なものに限らず異なるスケールのトレーニングデータに適応させることを可能にしている.
2.2 Multi-Grained Scanning
(※訳者注1)
ディープニューラルネットワークは,例えば,畳込みニューラルネットワークが生ピクセル間の空間的な関係が重要な画像データに対して効率的であり[LeCunら., 1998; Krizhenvskyら., 2012],リカレントニューラルネットワークが系列間の関係が重要な系列データに対して効率的であるるように,特徴間の関係を扱うのに長けている[Gravesら., 2013; Choら., 2014].この認識を元に,カスケードフォレストをmulti-grained scanning の手法で拡張した.
図3に示すように,生の特徴をスキャンするのにスライディングウィンドウを使用する.400個の特徴があってウィンドウサイズは100とする.系列データに対しては,1つの特徴に対してスライディングウィンドウによって100次元の特徴ベクトルが生成される;合計で301個の特徴ベクトルが生成される.20×20で400ピクセルの画像のように空間的な関係がある特徴ならば,10×10のウィンドウが121個の特徴ベクトルを生成する(つまり,10×10のパネルが121枚となる.).正例/負例の訓練例から抽出された全ての特徴ベクトルは正例/負例のインスタンスとみなされる;それらはその後,2.1節でみたようにクラスベクトルを生成するのに使用される.:同じサイズのウィンドウから抽出されたインスタンスは完全ランダム決定木フォレストとランダムフォレストを訓練するのに使われ,その後,クラスベクトルが生成され,変換された特徴として結合される.図3に示すように,3つのクラスと100次元のウィンドウが使われるとする;その場合,各フォレストから301個の3次元クラスベクトルが出力され,元の400次元特徴ベクトルに対応する1806次元の変換された特徴ベクトルになる.
図3は1種類のサイズのウィンドウしか示していない.複数サイズのスライドウィンドウを使うことで,図4に示すように,最終的な変換された特徴ベクトルはより多くの特徴を含むことになる.
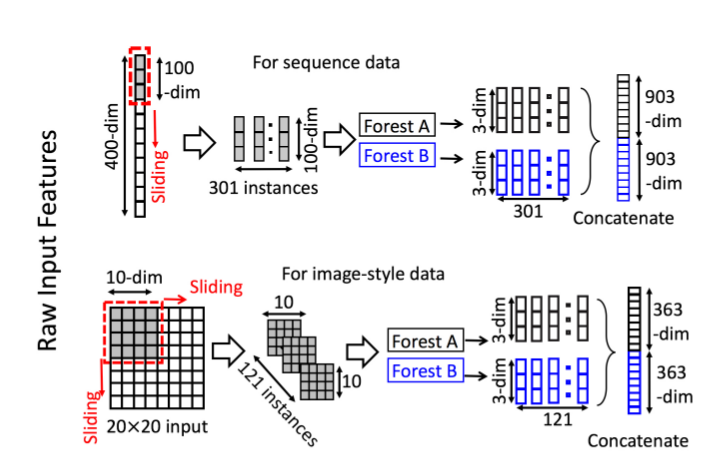
図3:スライディングウィンドウによるスキャンを使用した特徴の再表現を示す.3つのクラスがあり,生の特徴は400次元,スライディングウィンドウは100次元であるとする.
※訳者注1:Multi-Grained=「色々な種類を組み合わせている」
2.3 全体の流れとハイパーパラメータ
図4はgcForestの全体の流れを要約している.元の入力に400個の特徴があり,multi-grained scanningに3種類のウィンドウサイズが使われるとする.ウィンドウサイズ100は元の訓練例それぞれから301個の100次元特徴ベクトルを生成する;m個の訓練例があって,このスライドウィンドウが301×m個の100次元の訓練例を生成することになる.これらのデータは完全ランダム決定木フォレストとランダムフォレストを訓練するのに使用されるが,それぞれは30個の木を含む.予測すべきものが3クラスあるとする;各フォレストは3次元クラスベクトルを各301個のインスタンスに対して出力する.2つのフォレストから生成されたすべてのクラスベクトルを結合した後,1つの1806次元特徴ベクトルが得られる.
同様に,サイズ200とサイズ300のスライドウィンドウは1206次元と606次元の特徴ベクトルを,各訓練例に対して,それぞれ生成する.それらを結合することで,3618次元の特徴ベクトルが得られるが,それはmulti-grained scanningによる生の特徴ベクトルに対する再表現となっている.言い換えれば,元の各400次元特徴ベクトルは3618次元の特徴ベクトルによって再表現されている.
その後,m個の3618次元特徴ベクトルはカスケードへと渡される.セクション2.1で導入したように,カスケードの各階層が4つのフォレストから成るなら,カスケードの最初の階層の終わりで3630次元特徴ベクトルが得られる.これらの3630次元特徴ベクトルはその後カスケードの次の階層へと入力される;このプロセスはバリデーションパフォーマンスがカスケードの拡張を終了すべきことを示すまで繰り返される.
テスト用インスタンスを受け取った場合,そのインスタンスは対応する3618次元の特徴表現に成るべくmulti-grained scanningを通り,その後カスケードを最後の階層まで進む.最終的な予測は最後の階層での4つの3次元クラスベクトルを集約することで得られる.集約値が最大となるクラスを選択する.
表1はディープニューラルネットワークとgcForestのハイパーパラメータを要約したものだが,デフォルト値は私達の実験で使用したものを掲載した.
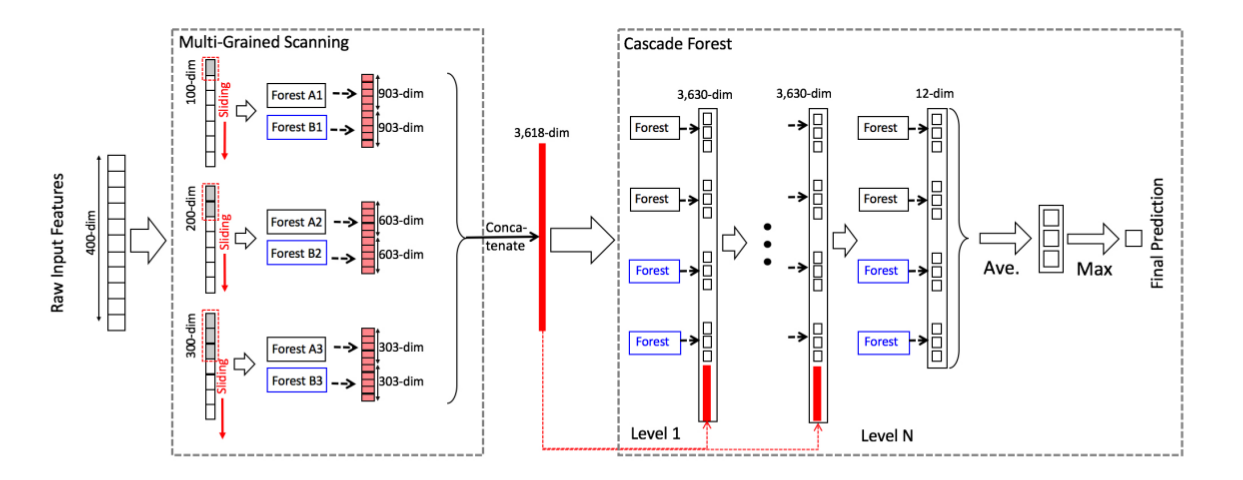
図4:gcForestの手順全体.予測すべき3つのクラスがあり,生の特徴は400次元,3種類のスライディングウィンドウが使用されている.
3 実験
3.1 設定
本セクションではgcForestとディープニューラルネットワークその他いくつかの人気のある学習アルゴリズムとを比較する.gcForestがより簡単なパラメータチューニングで,異なるタスクをまたいだ場合でさえもディープニューラルネットワークと高度に互角な性能を達成できることを示すことが目的である.それ故に,すべての実験でgcForestは同じカスケード構造を使用した:各階層は2つの完全ランダム決定木フォレストと2つのランダムフォレストから成り,それぞれが,セクション2.1で説明したように1000個の木を含む.クラスベクトルの生成には3分割(three-fold)クロスバリデーションを使用する.カスケードの階層数は自動的に決定される.より詳細には,私達はトレーニングセットを2つの部分に分割した.すなわち育成セットと推定セット(growing set and estimating set)である1.その後育成セットをカスケードの育成に使用し,推定セットを性能の推定に使用した.もし新しい階層を育成しても性能が改善しない場合は,カスケードの育成は終了し推定された数の階層が得られる(the estimated number of levels is obtained).その後,カスケードは育成セットと推定セットをマージしたもので再度訓練される.すべての実験で,訓練データの80%を育成セットに,20%を推定セットに使用した.multi-grained scanningについては,d個の生の特徴に対して,⌊d/16⌋,⌊d/9⌋,⌊d/4⌋(※訳者注2)の3つのウィンドウサイズを使用した;もし生の特徴が(画像のような)パネル構造なら,図3に示すように特徴ウィンドウもまたパネル構造である.慎重なチューニングはより良いパフォーマンスに繋がるだろう;しかし,今回は計算資源と詳細にハイパーパラメータをチューニングする時間が十分に得られなかった.それにもかかわらず,ファインチューニングを行わずに同じパラメータ設定を使用した場合でさえ,gcForestが優れた性能を達成することを発見した.
ディープニューラルネットワークの設定については,活性化関数にReLU,誤差関数にクロスエントロピー,最適化にAdaDelta,訓練データの数に応じて隠れ層のドロップアウト率0.25又は0.5などを使う.ところが,ネットワーク構造とハイパーパラメータは,タスクをまたいで同じとはならず,さもなければ呆れるほど性能が悪くなる.例えば,あるネットワークはADULTデータセットで80%の精度(accuracy)を達成したが,その同じアーキテクチャ(入出力ノード数のみデータに応じて変更する)はYEASTデータセットではたったの30%しか達成しない.したがって,ディープニューラルネットワークでは,検定セットで色々なアーキテクチャを調べ,最も性能の良いものを選択し,その後ネットワーク全体を訓練セットで再学習し,テストでの精度を報告する.
表1:ハイパーパラメータとデフォルト設定の要約.太字は比較的影響の大きいハイパーパラメータを強調している;"?"はデフォルト値が未知であるもの.

1 実験データセットのなかには訓練/検定(training/validation)用のデータセットを提供しているものがある.混乱を避けるため,ここでは訓練データから生成されたサブセットを育成/推定セットと呼ぶ.
※訳者注2:”⌊⌋”記号は床関数を表す
3.2 結果
画像分類
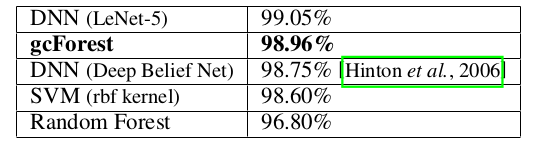
MNISTデータセット[LeCunら., 1998]は訓練用(と検定用)に60000枚,テスト用に10000枚の28×28画像を含む.LeNet-5(ドロップアウトとReLUを使用したLeNetの現代版),rbfカーネルのSVM,2000個の木による通常のランダムフォレストとの比較を行った.[Hintonら., 2006]で報告されたDeep Belief Netsの結果も掲載した.テスト結果は表2のようになり,単に表1に示したデフォルト設定を使用したgcForestが高度に互角な性能を達成していることを示している.
表2: MNISTデータセットでのテストaccuracyの比較
顔認識
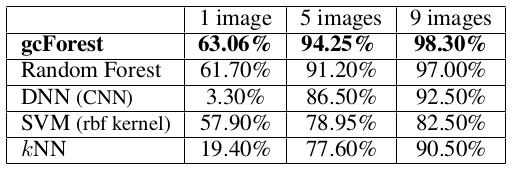
ORLデータセット[Samaria および Harter, 1994]は40人から撮影された400枚の白黒の顔画像を含む.3×3カーネルで32フーチャマップを生成する2つの畳み込み層から成るCNNと比較した.各畳み込み層の後には2×2のmax-pooling層が続く.128隠れユニットを持つ密結合層が畳み込み層と全結合し,最後に40隠れユニットを持つ全結合のソフトマックス層が追加される.ReLU,クロスエントロピー誤差,ドロップアウト0.25とAdaDeltaが訓練に使用される.バッチサイズは10,エポック数は50とした.CNNは別の設定も試したが,これが最も良い性能を示した.訓練では1人につきランダムに1/5/9枚の画像を選択し,残りの画像でテストの性能を報告する.40の可能な出力結果があるため,ランダム推定では2.5%の精度である.k=1のkNN法を訓練例に,3を残りのケースで使用した.テスト結果は表3にまとめた.
一人につき1つだけの訓練例が与えられた場合,CNNは訓練例不足で非常に低い性能しか示さなかった2.一方gcForestは,たとえ表2で使用されたのと同じ設定を使用しても,3つすべてのケースにおいて上手く実行された.
2CNNを使用して顔認識で素晴らしい性能示した研究が存在するが,それらは大量の顔画像をモデルの訓練に使用している.ここでは,私達は単に訓練データのみを使用する.
音楽分類
GTZANデータセット[Tzanetakis および Cook, 2002]は10ジャンルのミュージッククリップを含んでおり,それぞれが30秒の長さで100トラックとなっている.データセットを700クリップの訓練データと300クリップのテストデータに分割した.加えて,それぞれの30秒のミュージッククリップを表現するのにMFCC特徴量を使用した.これは元の音波を1280×13の特徴行列へ変換する.それぞれのフレームはその性質上不可分である(Each frame is atomic according to its own nature);そのため,CNNは畳み込み層にサイズ13×8のカーネルと32個のフィーチャマップを使用し(CNN uses a 13 × 8 kernel with 32 feature maps as the conv-layer),各層の後にはプーリング層が続く.1024および512ユニットを持つ2つの全結合層がそれぞれ追加され,最後にソフトマックス層が加わる.それぞれ1024と512ユニットの2つの隠れ層を持つMLPも比較対象とした.どちらのネットワークも活性化関数にReLU,誤差関数に分類型(categorical)クロスエントロピーを使用する.ランダムフォレスト,ロジスティック回帰,SVMについて,それぞれ入力は1280×13特徴ベクトルへと結合される.テスト結果は表4にまとめた.
表4: GTZANデータセットでのテストaccuracyの比較
手の動き認識
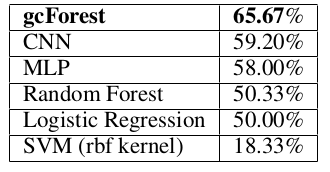
sEMGデータセット[Sapsanisら., 2013]はそれぞれが6つの手の動き(球状,先端,手のひら,片側,円筒形,引っ掛ける)(spherical, tip, palmar, lateral, cylindrical and hook)のうち1つに属する1800個の記録から成る(※訳者注3).筋電図センサが1秒に500個の特徴を捉えた時系列データであり,それぞれの記録は3000個の特徴と関連づく.入力-1024-512-出力構造のMLPに加えて,リカレントニューラルネットワークであるLSTM[Gersら.,2001]も評価した.ここでは128個の隠れユニットを持ち,シーケンス長6(1秒に500次元の入力ベクトル)である.テスト結果は表5にまとめた.
表5: sEMGデータセットでのテストaccuracyの比較
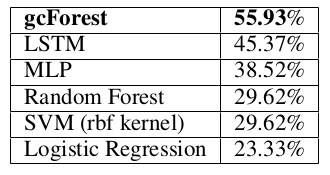
※訳者注3:sEMG=表面筋電位(surface electromyography)
感情分析
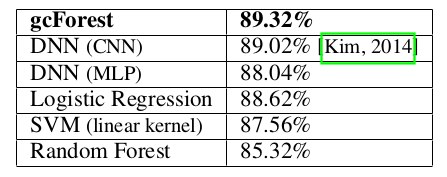
IMDBデータセット[Maasら., 2011]は訓練用/テスト用にそれぞれ25000個の映画レビューを含む.レビューはtf-idf特徴量で表現されている.画像データではないので,CNNは直接適用できない.そこで入力-1024-1024-512-256-出力のMLPと比較する.また,[Kim, 2014]に報告された結果も含めたが,そこでは単語埋め込みを使ってCNNを使用している.tf-idf特徴量は空間的な関係を伝達しないことを考え,gcForestでmulti-grained scanning は実行しなかった.
表6: IMDBデータセットでのテストaccuracyの比較
小規模データ
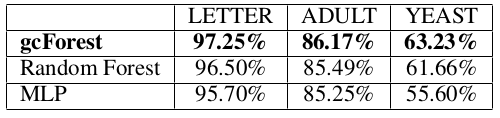
比較的小規模なUCIデータセット[Lichman, 2013]でもgcForestを評価した:すなわち特徴の数が16で16000/4000の訓練/テスト例を持つLETTER,特徴の数が14で32561/16281の訓練/テスト例を持つADULT,特徴の数がたったの8個で1038/446の訓練/テスト例を持つYEASTである.CNNのような派手な(fancy)アーキテクチャは,このように空間的な関係がなく,特徴の数が少なすぎるデータには不向きであることは明らかである.そこでMLPとの比較を行った.残念なことに,MLPは設定の選択肢がCNNより少ないが,それでもなお設定がとてもトリッキーである.例えば,入力−16−8−8−出力の構造とReLU活性化関数のMLPはADULTデータセットで76.37%のaccuracyを達成したがLETTERデータセットではたった33%だった.私達はすべてのデータセットでまともな性能を出すMLP構造を1つ選ぶことは不可能だと結論づけた.したがって,私達が考えることができた最高性能の,異なるMLP構造を報告する:LETTERでは入力−70−50−出力,ADULTでは入力−30−20−出力,YEASTでは入力−50−30−出力である.対照的に,gcForestはこれらの小規模データは空間的または時系列的な関係を保持していないと考えてmulti-grained scanningの使用をやめたこと以外は前と同じ設定を使用している.テスト結果は表7にまとめた.
3.3 Multi-Grained Scanningの影響
gcForestは2つの重要な構成要素を持つ.つまり,カスケードフォレストとmulti-grained scanningである.これらの寄与を別々に調査するため,表8はMNIST, GTZANおよびsEMGデータセットでのgcForestとカスケードフォレストの結果を比較している.空間的または系列的な特徴の関係が存在する際には,multi-grained scanning手法は性能を大きく改善することが明らかである.
表8: multi-grained scanning 有り/無しでのgcForestの結果

3.4 実行時間
実験ではIntel E5 2670 v3 CPU (24コア)を2個搭載したPCを使用し,gcForestの実行効率は非常に良かった.例えば,IMDBデータセット(25000訓練例,特徴数5000)では1つのカスケード階層に269.5秒(フォレストが4つあり,3-fold育成する),また,4つのカスケード階層で自動的に終了したが,これに1078秒つまり17.9分かかった.対照的に,前のセクションで述べた同じデータセットに対するMLPについては,ディープラーニング市場で最も強力なGPU(Nvidia Titan X pascal)で1エポックごとに14秒(バッチサイズは32)で,収束に50エポックを必要とし,訓練には700秒つまり11.6分を要した:CPUを使った場合,1エポックごとに93秒であり,4650秒つまり77.5分となる.完全ランダム決定木フォレストとランダムフォレストどちらも並列アンサンブル法 [Zhou, 2012]であることを注意しておく.それ故に,gcForestの効率性の利点は大規模な並列実装(large-scale parallel implementation)の場合に一層明らかとなる.
4 関連研究
gcForestは決定木アンサンブル手法である.アンサンブル法は強力な機械学習テクニックの一つであり,同一のタスクに対して複数の学習器を組み合わせるものである.実際にランダムフォレストのようなアンサンブル手法をディープニューラルネットワークの特徴量で推進(facilitated)することで,単にディープニューラルネットワークを使用するよりも性能改善が見込めることを示した研究が存在する[Peterら., 2015].アンサンブルを使う私達の目的は,しかし,大いに異なっている.私達はディープニューラルネットワークとの組み合わせよりもディープニューラルネットワークの代替となることを企図している.特に,カスケードフォレスト構造を使うことで,表現学習だけでなく,適したモデルの複雑さを自動的に決定することをも意図している.
学習器の1つのレベルの出力を別のレベルの学習器へ入力として渡すことはスタッキング[Wolpert,1992; Breiman,1996]と関連する.スタッキングに関する研究[Ting および Witten, 1999;Zhou, 2012]に示唆され,1つの階層から次へと入力を生成するのにクロスバリデーションの手順を使った.カスケードの手順はブースティング[Freund およびSchapire, 1997]に関連しているが,そちらは自動的にアンサンブル中の学習器の数を決定することができる.そして特に,カスケードブースティング手順[Vi-ola および Jones, 2001]は物体検出タスクで素晴らしい成功を収めた.カスケードの各レベルはアンサンブルのアンサンブルであるとみなせる;ブースティングのためにベース学習器にバギングを使用していた先行研究[Webb, 2000]とは対照的に,gcForestは特徴の再表現のために,アンサンブルを同じ階層で使用する.良いアンサンブルを構築するためには,個別の学習器が正確でかつ多様でなければならないことが知られている.ところが,今日まで広く受け入れられた多様性の形式的な定義が存在せず[Kuncheva および Whitaker, 2003; Zhou, 2012],私達が異なるタイプのフォレストをカスケードフォレストの各レベルで使ったように,研究者はいつも多様性を経験的に(heuristically)増やそうと試みてきた.
multi-grained scanning はデータを検証するのに異なるサイズのスライディングウィンドウを使用する;これは幾らかウェーブレット及びその他の複数解像度(multi-resolution)の検証手法に関連している[Mallat, 1999].各ウィンドウサイズについては,インスタンスのセットが1つの訓練例から生成される;これはマルチインスタンス学習[Dietterich ら., 1997]のbag生成器(bag generators)と関連している[Wei および Zhou, 2016].特に,図3の下段部分は画像に対して適用されると,SB image bag生成器[Maron および Lozano-Pérez,1998; Wei および Zhou, 2016]とみなせる.
5 結論
ディープラーニングの鍵は表現学習とモデルの大容量さにあるとの認識に基づき,本論文ではそれらの資産を決定木アンサンブルへ与えることを試み,gcForest法を提案した.実験において,gcForestはディープニューラルネットワークと比べて互角またはより優れた性能を達成した.更に重要なことに,gcForestはハイパーパラメータがより少なく,パラメータセッティングに対して敏感ではない;実際,実験において様々なドメインにまたがって同じパラメータ設定を使用しても素晴らしい性能が得られており,大規模データでも小規模データでも問題なく良く動作する.さらに,本論文の範囲からは外れるが,決定木ベースアプローチなのでgcForestはディープニューラルネットワークよりも論理的な解析が容易である.gcForestのコードはすぐに利用できるようにする.
ディープフォレストの構成方法は他にも可能性がある.セミナー研究(seminar study)として,この方向についての探索は少量にとどめた.もし強力な計算設備があれば大量データとよりディープなフォレストを試したいが,それは今後の課題である.原則的に,ディープフォレストは特徴抽出器としての動作や事前学習モデルなどディープニューラルネットワークが持つ他の能力を示すことも可能であるはずだ.複雑なタスクに取り組むには学習モデルはディープにならざるを得ないことは特筆に値する.しかし,現在のディープモデルはいつもニューラルネットワークばかりである.本論文はディープフォレストの構成法を説明したが,私達はそれが多くのタスクにおいてディープニューラルネットワークの代替へと向かう扉を開くことを信じている.
謝辞:
本論文の草稿を読んで頂いたSongcan Chen, Xin Geng, Sheng-Jun Huang, Chao Qian, Jianxin Wu, YangYu, De-Chuan Zhan, Lijun Zhang, Min-Ling Zhangに対して感謝の意を表したい.
引用文献
[Breiman, 1996] L. Breiman. Stacked regressions. Machine Learning, 24(1):49–64, 1996.
[Breiman, 2001] L. Breiman. Random forests. Machine Learning, 45(1):5–32, 2001.
[Choら., 2014] K. Cho, B. van Meriënboer, C. Gulcehre, D. Bahdanau, F. Bougares, H. Schwenk, and Y. Bengio. Learning phrase representations using RNN encoder-decoder for statistical machine translation. In 2014 Conference on Empirical Methods in Natural Language Processing, pages 1724–1734, 2014.
[Dietterichら., 1997] T. G. Dietterich, R. H. Lathrop, and T. Lozano-Pérez. Solving the multiple-instance problem with axis-parallel rectangles. Artificial Intelligence, 89(1-2):31–71, 1997.
[Freund および Schapire, 1997] Y. Freund and R. E. Schapire. A decision-theoretic generalization of on-line learning and an application to boosting. Journal of Computer and System Sciences, 55(1):119–139, 1997.
[Gersら., 2001] F. A. Gers, D. Eck, and J. Schmidhuber.Applying LSTM to time series predictable through time-window approaches. In International Conference on Artificial Neural Networks, pages 669–676, 2001.
[Goodfellowら., 2016] I. Goodfellow, Y. Bengio, and A. Courville. Deep Learning. MIT Press, Cambridge,MA, 2016.
[Gravesら., 2013] A. Graves, A. R. Mohamed, and G. Hinton. Speech recognition with deep recurrent neural networks. In 38th IEEE International Conference on Acoustics, Speech and Signal Processing, pages 6645–6649, 2013.
[Hintonら., 2006] G. E. Hinton, S. Osindero, and Y.-W.Simon. A fast learning algorithm for deep belief nets. Neural Computation, 18(7):1527–1554, 2006.
[Hintonら., 2012] G. Hinton, L. Deng, D. Yu, G. Dahl, A. Mohamed, N. Jaitly, A. Senior, V. Vanhoucke, P. Nguyen, T. Sainath, and B. Kingbury. Deep neural networks for acoustic modeling in speech recognition. IEEE Signal Processing Magazine, 29(6):82–97, 2012.
[Kim, 2014] Y. Kim. Convolutional neural networks for sentence classification. arXiv:1408.5882, 2014.
[Krizhenvskyら., 2012] A. Krizhenvsky, I. Sutskever, and G. Hinton. ImageNet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems 25, pages 1097–1105. 2012.
[Kuncheva および Whitaker, 2003] L. I. Kuncheva and C. J.Whitaker. Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy. Machine Learning, 51(2):181–207, 2003.
[LeCunら., 1998] Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
[Lichman, 2013] M. Lichman. UCI machine learning repository, 2013.
[Liuら., 2008] F. T. Liu, K. M. Ting, Y. Yu, and Z.-H.Zhou. Spectrum of variable-random trees. Journal of Artificial Intelligence Research, 32:355–384, 2008.
[Maasら., 2011] A. L. Maas, R. E. Daly, P. T. Pham, D. Huang, A. Y. Ng, and C. Potts. Learning word vectors for sentiment analysis. In 49th Annual Meeting of the Association for Computational Linguistics, pages 142–150, 2011.
[Mallat, 1999] S. Mallat. A Wavelet Tour of Signal Processing. Academic Press, London, UK, 2nd edition, 1999.
[Maron および Lozano-Pérez, 1998] O. Maron and T. Lozano-Pérez. A framework for multiple-instance learning. In Advances in Neural Information Processing Systems 10, pages 570–576. 1998.
[Peterら., 2015] K. Peter, F. Madalina, C. Antonio, and R. Samuel. Deep neural decision forests. In IEEE International Conference on Computer Vision, pages 1467–1475, 2015.
[Samaria および Harter, 1994] F. Samaria and A. C. Harter. Parameterisation of a stochastic model for human face identification. In 2nd IEEE Workshop on Applications of Computer Vision, pages 138–142, 1994.
[Sapsanisら., 2013] C. Sapsanis, G. Georgoulas, A. Tzes,and D. Lymberopoulos. Improving EMG based classification of basic hand movements using EMD. In 35th Annual International Conference on the IEEE Engineering in Medicine and Biology Society, pages 5754–5757, 2013.
[Simonyan および Zisserman, 2014] K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556, 2014.
[Ting および Witten, 1999] K. M. Ting and I. H. Witten. Issues in stacked generalization. Journal of Artificial Intelligence Research, 10:271–289, 1999.
[Tzanetakis および Cook, 2002] G. Tzanetakis and P. R. Cook. Musical genre classification of audio signals. IEEE Trans. Speech and Audio Processing, 10(5):293–302, 2002.
[Viola および Jones, 2001] P. Viola and M. Jones. Rapid object detection using a boosted cascade of simple features. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pages 511–518, 2001.
[Webb, 2000] G. I. Webb. MultiBoosting: A technique for combining boosting and wagging. Machine Learning, 40(2):159–196, 2000.
[Wei および Zhou, 2016] X.-S. Wei and Z.-H. Zhou. An empirical study on image bag generators for multi-instance learning. Machine Learning, 105(2):155–198, 2016.
[Wolpert, 1992] D. H. Wolpert. Stacked generalization. Neural Networks, 5(2):241–260, 1992.
[Zhou, 2012] Z.-H. Zhou. Ensemble Methods: Foundations and Algorithms. CRC, Boca Raton, FL, 2012.