Rで条件付き分布の計算とベイジアンネットワークの描画

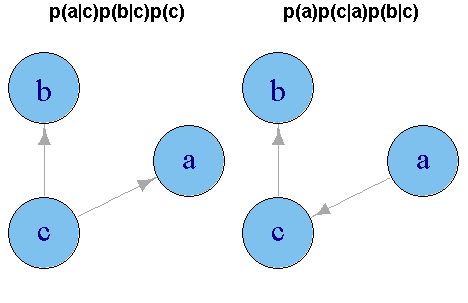
PRML演習8.3の通り、与えられた2値変数a,b,cの同時分布から、aとbが独立でなく、cのもとで条件付き独立であることを確認し、p(a,b,c)=p(a,b|c)p(c)=p(a|c)p(b|c)p(c)に対応するベイジアンネットワークを描画します。また、演習8.4の通り、同時分布がp(a,b,c)=p(a)p(c|a)p(b|c)とも因数分解できることを確認し、対応するベイジアンネットワークを描画します。

  a b p(a,b) p(a)p(b) p(a,b|c=0) p(a|c=0)p(b|c=0) p(a,b|c=1) p(a|c=1)p(b|c=1)
1 0 0  0.336   0.3552        0.4              0.4  0.2769231        0.2769231
2 0 1  0.264   0.2448        0.1              0.1  0.4153846        0.4153846
3 1 0  0.256   0.2368        0.4              0.4  0.1230769        0.1230769
4 1 1  0.144   0.1632        0.1              0.1  0.1846154        0.1846154
  a b c     p p(a|c)p(b|c)p(c) p(a)p(c|a)p(b|c)
1 0 0 0 0.192            0.192            0.192
2 0 0 1 0.144            0.144            0.144
3 0 1 0 0.048            0.048            0.048
4 0 1 1 0.216            0.216            0.216
5 1 0 0 0.192            0.192            0.192
6 1 0 1 0.064            0.064            0.064
7 1 1 0 0.048            0.048            0.048
8 1 1 1 0.096            0.096            0.096

library(igraph)
frame()
set.seed(0)
par(mfcol=c(1, 2))
par(mar=c(0, 0, 1, 0))

d <- data.frame(matrix(c(
    0, 0, 0, 192,
    0, 0, 1, 144,
    0, 1, 0, 48,
    0, 1, 1, 216,
    1, 0, 0, 192,
    1, 0, 1, 64,
    1, 1, 0, 48,
    1, 1, 1, 96
    ), ncol=4, byrow=T))
names(d) <- c("a", "b", "c", "p")
d$p <- d$p / 1000

# p(a,b)
dab <- data.frame()
for (a in 0:1) {
    for (b in 0:1) {
        pa <- sum(d[d$a == a,]$p) # p(a)
        pb <- sum(d[d$b == b,]$p) # p(b)
        dab <- rbind(dab, c(
            a, 
            b, 
            sum(d[d$a == a & d$b == b,]$p), 
            pa * pb
            ))
    }
}
names(dab) <- c("a", "b", "p(a,b)", "p(a)p(b)")

# p(a,b|c)
for (a in 0:1) {
    for (b in 0:1) {
        for (c in 0:1) {
            pc <- sum(d[d$c == c,]$p) # p(c)
            pabc <- sum(d[d$a == a & d$b == b & d$c == c,]$p) / pc
            dab[dab$a == a & dab$b == b, paste0("p(a,b|c=", c, ")")] <- pabc
            pac <- sum(d[d$a == a & d$c == c,]$p) / pc # p(a|c)
            pbc <- sum(d[d$b == b & d$c == c,]$p) / pc # p(b|c)
            dab[dab$a == a & dab$b == b, paste0("p(a|c=", c, ")p(b|c=", c, ")")] <- pac * pbc
        }
    }
}
print(dab)

# p(a,b,c)=p(a|c)p(b|c)p(c)
for (i in 1:nrow(d)) {
    pc <- sum(d[d$c == d[i,]$c,]$p) # p(c)
    pac <- sum(d[d$a == d[i,]$a & d$c == d[i,]$c,]$p) / pc # p(a|c)
    pbc <- sum(d[d$b == d[i,]$b & d$c == d[i,]$c,]$p) / pc # p(b|c)
    d[i,"p(a|c)p(b|c)p(c)"] <- pac * pbc * pc
}
g1 <- graph(c(3, 1, 3, 2))
V(g1)$size <- 100
V(g1)$label.cex <- 2
V(g1)$label <- letters[1:3]
plot(g1, layout=layout.circle)
title("p(a|c)p(b|c)p(c)")

# p(a,b,c)=p(a)p(c|a)p(b|c)
for (i in 1:nrow(d)) {
    pa <- sum(d[d$a == d[i,]$a,]$p) # p(a)
    pc <- sum(d[d$c == d[i,]$c,]$p) # p(c)
    pca <- sum(d[d$c == d[i,]$c & d$a == d[i,]$a,]$p) / pa # p(c|a)
    pbc <- sum(d[d$b == d[i,]$b & d$c == d[i,]$c,]$p) / pc # p(b|c)
    d[i,"p(a)p(c|a)p(b|c)"] <- pa * pca * pbc
}
g2 <- graph(c(1, 3, 3, 2))
V(g2)$size <- 100
V(g2)$label.cex <- 2
V(g2)$label <- letters[1:3]
plot(g2, layout=layout.circle)
title("p(a)p(c|a)p(b|c)")

print(d)