Ex2.11
;ついでに Ben はまた謎めいたコメントを残した。
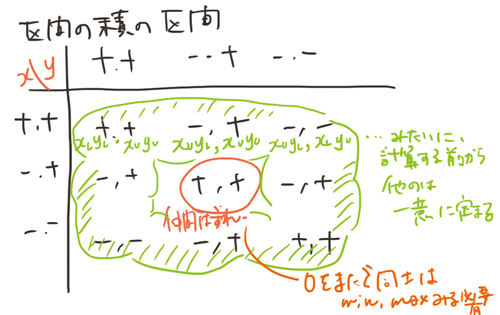
;“区間の両端点の符号をテストすると mul-interval は 9 パターン
;に場合分けできて、2 回以上のかけ算が必要になるのはその中のひ
;とつだけだよ。” Ben の提案に従って、この手続きを書き直せ。
ここの図がわかりやすい:http://www.serendip.ws/archives/553
(define (make-center-width c w)
(make-interval (- c w) (+ c w)))
(define (center i)
(/ (+ (lower-bound i) (upper-bound i)) 2))
(define (width i)
(/ (- (upper-bound i) (lower-bound i)) 2))
Ex 2.12
;; Ex 2.12
;; SAMPLE
(define interval-pp (make-interval 9.0 11.0))
(define interval-mp (make-interval -2.0 2.0))
(define interval-mm (make-interval -10.0 -2.0))
;; 中央値と%の許容誤差を取る
(newline)
(display "=========Ex 2.12==========")
(newline)
(define (percent i)
(* (/ (width i) (center i)) 100))
(define (make-center-percent i)
(cons (center i) (percent i)))
(define (print-center-interval i)
(print "[ " (car i) "±" (cdr i) "%" " ]\n"))
(print-interval interval-pp)
(print-center-interval (make-center-percent interval-pp))
;9. ~ 11.
;[ 10.±10.% ]
(print-interval interval-mp)
(print-center-interval (make-center-percent interval-mp))
;-2. ~ 2.
;[ 0.±+inf.0% ]
Ex 2.13
;; 2.13
; パーセント許容誤差が小さいという前提のもとで
;は、二つの区間の積のパーセント許容誤差を因数の許容誤差の積
;によって近似する簡単な式が存在することを示せ。すべての数値
;は正であると仮定して問題を単純化してもよい。
;意味がわからない(((((((((((っ・ω・)っ
Ex 2.14
;; 2.14
(newline)
(display "=========Ex 2.14==========")
(newline)
(define A (make-interval 6 10))
(define B (make-interval 19.0 21.0))
(print "A:")
(print-center-interval (make-center-percent A))
(print "B:")
(print-center-interval (make-center-percent B))
(print "par1: ")
(print-interval (par1 A B))
(print "par2: ")
(print-interval (par2 A B))
;par1: 3.6774193548387095 ~ 8.4
;par2: 4.5600000000000005 ~ 6.774193548387097
(print "A/A: ")
(define AA (div-interval A A))
(print-interval AA)
;; これが1にならない
(print "A/B: ")
(define AB (div-interval A B))
(print-interval (make-center-percent AB))
;A/A: 1.1333333333333333 ~ 47.058823529411754
;A/B: .40601503759398494 ~ 29.629629629629626
以下メモ


2.15
「変数が繰り返し出てこないように書くほどより厳密な誤差限界を返すようにできる」は真か
区間に対して四則演算をすればするほど差は解の区間は大きくなる
widthが演算後に小さくなることはない。
とはいえ、加算と乗算で誤差の広がる範囲が同じわけでもないし、
一概に区間が出てくる回数が少ないほど小さいと言えるわけでもない・・・??
と思ったけど、問題の趣旨は、
代数として等価な式であれば、
区間が少ないほうが誤差が小さい
ってことかな?
R1 を区間としたときに
- R1 / R1 よりも 1のほうが誤差がない
- (R1 * R1) / R1 よりも R1のほうが誤差ができない
(newline)
(display "=========Ex 2.15==========")
(newline)
(newline)
(display "========= diff > 1 ==========")
(newline)
(define i1 (make-interval 5.0 7.0)) ;width 1
(define i2 (make-interval -5 -2))
(print (width (add-interval i1 i2)) "\n")
(print (width (mul-interval i1 i2)) "\n")
(print (width (sub-interval i1 i2)) "\n")
(print (width (div-interval i1 i2)) "\n")
(newline)
(display "========= diff < 1 ==========")
(newline)
(define i1 (make-interval 1 5)) ;width2
(define i2 (make-interval 1 1.2))
(print (width (add-interval i1 i2)) "\n")
(print (width (mul-interval i1 i2)) "\n")
(print (width (sub-interval i1 i2)) "\n")
(print (width (div-interval i1 i2)) "\n")
;========= diff > 1 ==========
;2.5
;12.5
;2.5
;1.25
;全部元のwidth(1)以上
;========= diff < 1 ==========
;2.1
;2.5
;2.1
;2.0833333333333335
;全部元のwidth(2)以上
2.16
次回に繰越