(2015/07/15 9:30 追記)
結論から言うと、球面上に一様分布する関数を使うことで分散できたので、最終的なコードも含めていちばん最後に追記しました。
最近Processingで遊んでいて、「3D空間に三角関数を使ったプロットをいっぱい置いて球面を作る」というコードを書いていたんだけど、一部にプロットが集まってきてしまうのが気になっていた(ちょっとわかりにくいけど、下の画像でいうと中心左寄りの部分)。
そこで、乱数の生成処理を工夫して、ある程度ランダムでプロットを置きつつも一部に集中してしまうのを回避しようといろいろ試してみたので、その内容をメモる。
(途中からそれって乱数なの?みたいな気分になってきたけど、考えがまとまらなくなりそうだったので気にしていません……。)
元々のコードはこんな感じ。このコード自体はこのサイトを参考にして作った。
private static final int PLOTS_COUNT = 3000;
private static final int RADIUS = 100;
private Plot[] plots = new Plot[PLOTS_COUNT];
void setup() {
size(250, 250, P3D);
// プロットを作成
for (int i = 0; i < PLOTS_COUNT; i++) {
plots[i] = new Plot();
}
// プロットの色と大きさ
stroke(0, 192, 255, 180);
strokeWeight(4);
}
void draw() {
background(0);
// 中心点を移動
translate(width/2, height/2, 0);
rotateY(frameCount*0.005);
rotateZ(frameCount*0.005);
for (Plot p : plots) {
point(p.x, p.y, p.z);
}
}
private class Plot {
final float x, y, z;
Plot() {
// 球面上の座標をランダムで計算
float radianS = radians(random(180));
float radianT = radians(random(360));
x = RADIUS * sin(radianS) * cos(radianT);
y = RADIUS * sin(radianS) * sin(radianT);
z = RADIUS * cos(radianS);
}
}
プロットが一部に集まってしまうのは、Z軸にcosを使って球体の赤道上にあたる部分を大きく、北極・南極の部分を小さく、という計算をしているため。
Z座標が0に近づくほどプロット感の開きが大きくなり、逆に遠ざかるほど密集してしまう。
各プロットのZ軸はradianSにより、0°〜180°をの中から完全にランダムで選び出している。
なので、この値が90°に近づくほど多めに出現する乱数生成器のようなものができれば、目的が達成できそう。
中央値に近いほど多く出現させる
まず考えたのは、乱数で中央値からの上下範囲を出してから、その範囲内で乱数を出現させる方法。
// 値の出現回数を棒グラフっぽく表示
void setup() {
size(180*2, 250);
background(255);
noLoop();
int[] counts = new int[180];
for (int i = 0; i < 100000; i++) {
float r = generateRandom1(180);
counts[(int)r]++;
}
stroke(0);
strokeCap(SQUARE);
for (int i = 0; i < 180; i++) {
line(i*2, height, i*2, height - counts[i] / 10);
}
stroke(224);
fill(0);
for (int i = 1; i < 5; i++) {
line(0, height-i*50, width, height-i*50);
text(i*500, 5, height-i*50);
}
}
// 乱数生成
float generateRandom1(float high) {
float range = random(0.5);
return random(high * range, high * (1 - range));
}
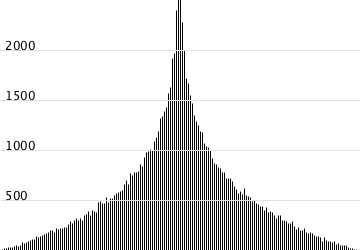
実行結果。右の画像は0°〜180°の各値の出現回数で、左は実際に球面上にプロットしてみたもの。90°に近くなるほど二次関数的に増えてしまい、プロットが天の川みたいになってしまった。これはこれでおもしろいけど今回やりたいこととはちょっと違う。
中央値から上下それぞれの出現範囲を乱数で決定する
中央値に寄り過ぎるとまずいので、中央値からの値の出現範囲を上下別々に乱数で生成し、その範囲内で乱数を出現させるようにしてみた。
float generateRandom2(float high) {
float min = high * random(0, 0.5);
float max = high * random(0.5, 1);
return random(min, max);
}
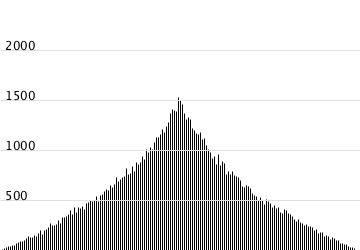
実行結果はこんな感じ。今度はグラフの勾配がだいぶ緩やかになった。球面上のプロットもだいぶ天の川感が解消されたように感じる。もう少しこの勾配を緩やかにする方法を考えてみる。
偏りの中央値を分散させた乱数をいくつか組み合わせて作る
今までの2つは90°を中央値として偏った乱数が発生するようなものを考えてきたが、指定した位置に向けて偏りのある乱数が発生するような処理を考えてみる。具体的にはこんな感じ。
// 乱数生成
float generateRandom3(float high, float bias) {
float min = high * random(0, bias);
float max = high * random(bias, 1);
return random(min, max);
}
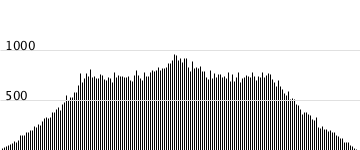
これを使って、45°, 90°, 135°のそれぞれの位置を中央値として、同じ数だけ生成した数を合わせてみると、こういうグラフになる。
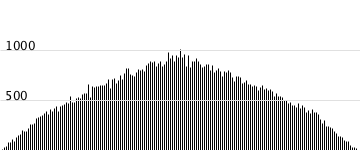
良さげ。このままだと変な位置にピークがあってまだ微妙な感じなので、もっと中央値にバリエーションを持たせて生成した乱数を組み合わせてみた。生成した乱数を扱う側はこういう感じになる。
// 値の出現回数を棒グラフっぽく表示
void setup() {
size(180*2, 200);
background(255);
noLoop();
float[] biases = {
0.125, 0.25, 0.35, 0.425, 0.475, 0.5, 0.525, 0.575, 0.65, 0.75, 0.875
};
int[] counts = new int[180];
for (int i = 0; i < 100000; i++) {
float bias = biases[i % biases.length];
float r = generateRandom3(180, bias);
counts[(int)r]++;
}
// 棒グラフ描く処理 ...
}
// 乱数生成
float generateRandom3(float high, float bias) {
float min = high * random(0, bias);
float max = high * random(bias, 1);
return random(min, max);
}
だいぶいい感じになってきた。あんまり偏ってる感じもないし、逆に整列している感じもない。
まとめ
中央値がピークになるような、なだらかなカーブを描く分布の乱数が生成できれば、かなりいい具合にプロットが分散できそうだなという感じです。
それと、ここまで来るとグラフの分布が正弦波に近い……ような気がしてきたので、乱数の分布が正弦波となるような乱数生成器ができればいちばん正解に近いのかな。
球面上に一様分布させる計算方法があった(追記)
これまでの考えは、平面上に分布したプロットを球面上に再配置するような計算をしていた。そもそも球面上に一様分布するような乱数の計算方法ってありそうだなと思って探したところ、見事に見つかった(これまで考えてきた時間はなんだったのか……)。
このPDF資料に、まさに単位球面に一様分布する点の計算方法がある。
今までの計算では、0°〜180°の一様分布からcosを使ってz軸の値を求めていた。cosの値の変化量は、0°、180°に近いほど少なく、90°に近いほど多くなるため偏りが出てしまう。
このため、まずz軸の値cos(θ)そのものを-1〜1の一様分布から取り出し、その値を元にsin(θ)を求めてx,yの値を決める。
$sin^2(θ) = 1 - cos^2(θ)$なので、x,y,z座標はそれぞれ下記の数式で求まる。
\begin{aligned}
x & = \sqrt{1 - z^2} * cos(φ) \\
y & = \sqrt{1 - z^2} * sin(φ) \\
z & = z
\end{aligned}
これを使って球面にプロットしてみる。コードと実行結果。
private static final int PLOTS_COUNT = 3000;
private static final int RADIUS = 100;
private Plot[] plots = new Plot[PLOTS_COUNT];
void setup() {
size(250, 250, P3D);
for (int i = 0; i < PLOTS_COUNT; i++) {
plots[i] = new Plot();
}
// プロットの色と大きさ
stroke(0, 192, 255, 180);
strokeWeight(4);
}
void draw() {
background(0);
// 中心点を移動
translate(width/2, height/2, 0);
rotateY(frameCount*0.005);
rotateZ(frameCount*0.005);
for (Plot p : plots) {
point(p.x, p.y, p.z);
}
}
private class Plot {
final float x, y, z;
Plot() {
// 球面上の座標をランダムで計算
float unitZ = random(-1, 1);
float radianT = radians(random(360));
x = RADIUS * sqrt(1 - unitZ * unitZ) * cos(radianT);
y = RADIUS * sqrt(1 - unitZ * unitZ) * sin(radianT);
z = RADIUS * unitZ;
}
}
きれいに分散した。この方法であれば乱数生成回数自体も抑えられるのでパフォーマンス的にも良さそう。