Qiitaでの初投稿です。
今までHPでまとめていたのですが、Qiitaの方がアップがしやすいので、少しずつこちらにTipsをまとめていきたいと思います。(①書きながらプレビューで記載内容が確認できる、②mathjaxも使える、③簡単に画像がアップできる、④目次が自動生成されるのは素晴らしいですね!)
手軽にアップできるので、HPよりも少し詳細に書いていきます。
私は職業柄、VBAで数値計算を行う機会が多いのですが、その中で特に役立った知見をご紹介します。
陽解法Eulerの安定限界
さて本題ですが、数値計算を行う際、重要になるのが計算刻みです。計算精度をよくするためには計算刻みを細かくしたいところですが、細かく刻みすぎると計算コストが高くなってしまいます。
一方で計算速度を上げようとして、刻みを粗くすると収束性が悪くなってしまいますし、場合によっては発散してしまう可能性があります。
ちょうど良いバランスを探す必要がありますが、例えば、陽解法Eulerであれば、一つの目安として安定性の限界条件があります。
陽解法Eulerの安定性限界は、計算刻み(Δt)を、系の最小時定数τminの2倍以下にする必要があるというものです。
2\cdot\tau_{min}\geq\Delta t
実際に陽解法Eulerの安定条件について、シンプルな2階常微分方程式の安定性をVBAで調べてみます。
確認式例
\frac{d^2y}{dt^2}+7\frac{dy}{dt}+6y=0
ただし、初期条件は、y(0)=2、y'(0)=-7とします。
まずはVBAで数値計算として求める前に上記の常微分方程式を解析的に求めておきます。
特性方程式は、
\lambda^2+7\lambda+6=0
\left(\lambda+6\right)\left(\lambda+1\right)=0
となりますので、一般解は、
C_1e^{-t}+C_2e^{-6t}=0
ちょっとはしょりますが、初期条件、y(0)=2、y'(0)=-7を代入して、解析解は以下になります。
e^{-t}+e^{-6t}=0
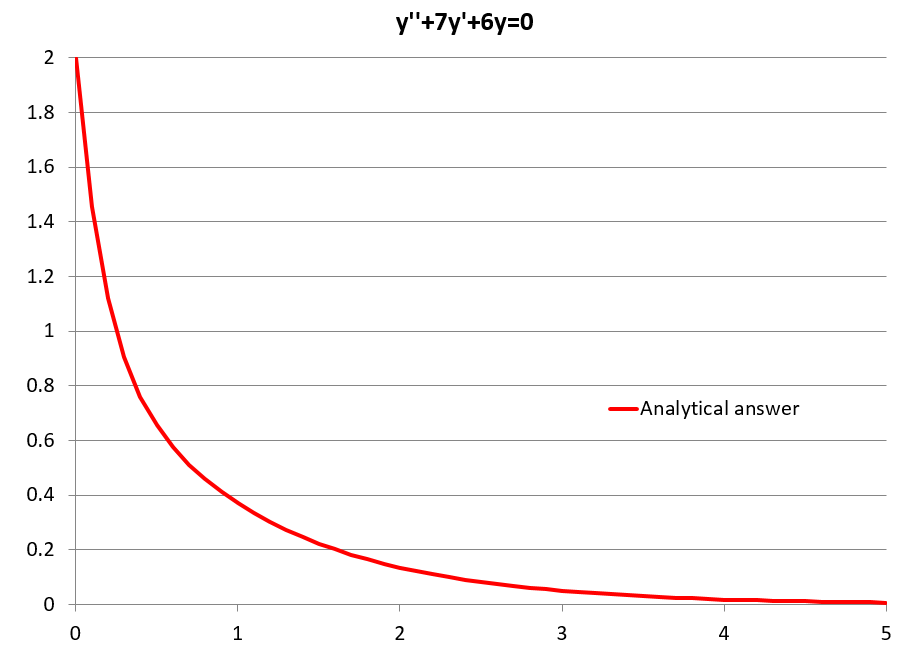
エクセルでプロットすると、上図のようになります。
大分前準備が長くなりましたが、いよいよVBAで数値計算上の安定限界を確認してみます。
VBAでの陽解法Eulerの実装
数値計算で求めるために、微分方程式を離散化していきます。
一気には解けないので、まず$\frac{dy}{dt}=u$とすると、以下の連立方程式に変換できます。
\frac{dy}{dt}=u
\frac{du}{dt}=-7u-6
続いて離散化していきます。
\frac{y_{n+1}-y{n}}{\Delta t}=u_n
\frac{u_{n+1}-u{n}}{\Delta t}=-7u_n-6y_n
整理すると、
y_{n+1}=y_n+u_n{\Delta t}
u_{n+1}=u_n-7u_n{\Delta t}-6y_n{\Delta t}
初期値は、y(0)=2, u(0)=-7なので、例えば時間刻みが0.2であれば、次のステップは
y_{1}=y(0)+u(0){\Delta t}=2-7*0.2=0.6
u_{1}=u(0)-7u(0){\Delta t}-6y(0){\Delta t}=-7-7*(-7)*0.2-6*2*0.2=0.4
では、上記の関係式をVBAで計算していきます。
VBAで計算する方法は色々考えられるかと思いますが、以下コードの一例です。
Dim y, py As Double
Dim u, pu As Double
Dim i, t, dt As Double
Dim n As Integer
n = 20
dt = 0.3
t = 0
py = 2
pu = -7
For i = 1 To n
y = py + pu * dt
u = pu - 7 * pu * dt - 6 * py * dt
Cells(1 + i, 1) = t
Cells(1 + i, 2) = y
Cells(1 + i, 3) = u
t = t + dt
py = y
pu = u
Next
$y_{n+1}$をy、$y_n$をpy、$u_{n+1}$をu、$u_n$をpuとして計算しています。
時間刻みを0.3とし、20time step分の計算を行っています。
t,y,uはそれぞれA~C列に順次入力していくようにしています。
上記のVBAを走らせると、以下のようになります。
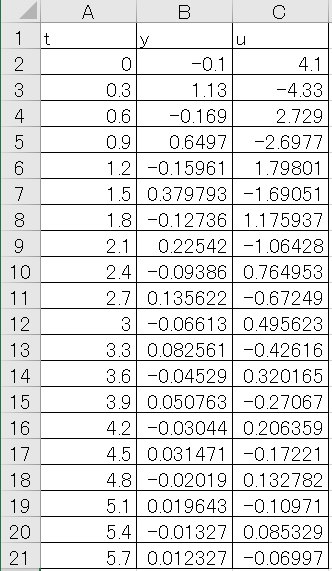
陽解法Eulerの安定性の確認結果
さて、本題の陽解法Eulerの安定性についてですが、解析解の形から分かるように、今回のケースでは、時定数が1、1/6ですので、最小の時定数$\tau _{min}$は、2/6=1/3以上である必要があります。
では、計算時間刻みを0.3、0.34とし時間変化を比較してみます。
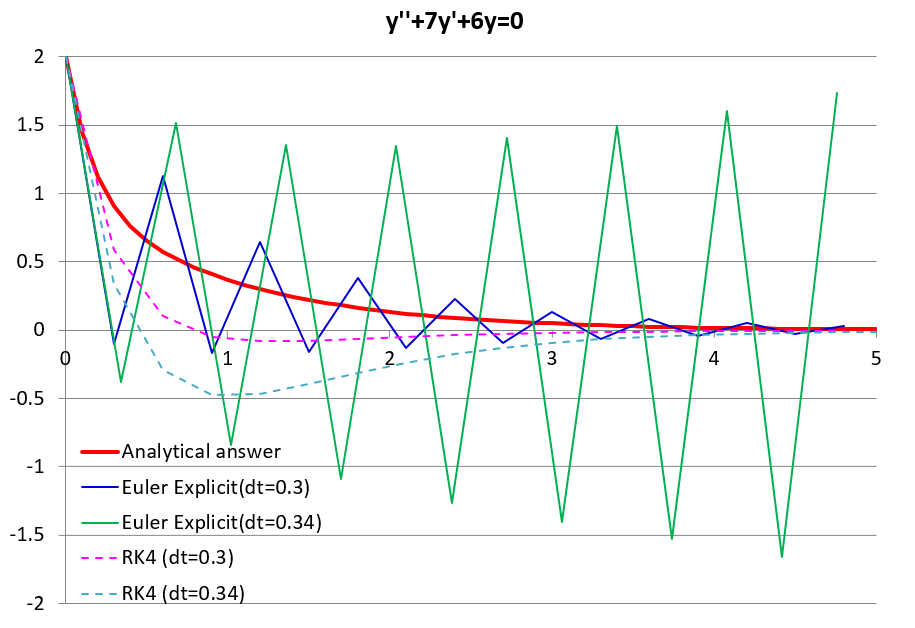
赤い線が解析解、緑の線が時間刻みを0.34secで、青い線が0.3secで計算した結果になります。
時間刻みを0.34secにしてしまうと徐々に計算が発散していってしまうことが確認できます。
ちなみに参考までに4次のRunge-Kuttaであれば、時間刻み0.34secでも発散しません。
陽解法Eulerの安定性限界が、「計算時間刻みを最小時定数の2倍以下にすること」であることが確認できました。
なお、陽解法Eulerの安定性限界が上記の条件となることは計算で導くことができます。
本稿では省きますが、興味のある方は以下の本を参照してみてください。
(4次のRunge-Kutta安定限界についても記載されています。)
Philip J Thomas,; ”Simulation of Industrial Processes for Control Engineers”; Butterworth-Heinemann, 1999