異常検知と変化検知 (機械学習プロフェッショナルシリーズ) の第6章の輪読資料です。
前節までの流れと本節
ホテリングのT2の異常検知では、単一の正規分布仮定で異常検知モデルを作った。その後、4~5章で局所データの散らばりに着目、近傍法、混合分布モデルにて異常検知モデルを作成した。今回扱うのは、ホテリングのT2の世界にもう一度戻って、異常検知を行う手法。
サポートベクトルデータによる異常検知の考え方
ラベルが与えられていないデータ
\quad \mathcal{D} = \bigl\{ {x^{(1)}, x^{(2)}, \cdots, x^{(N)}} \bigr\}
を考える。この中には異常標本は含まれていない、またはごく少数の前提。
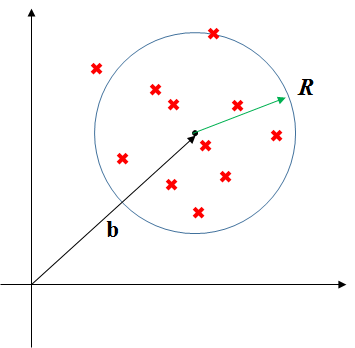
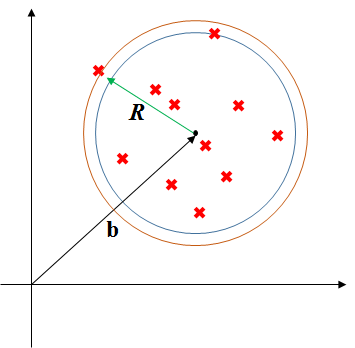
このデータDに対して、半径RにデータDを全て含む球を考え、最少のRを求める最適化問題
\min_{R^2, b} R^2 \quad subject \quad to \quad ||x^{{(n)}} - b||^2 \leq R^2 \\
ただし n=1 \cdots N ,\quad ||a|| = a^Ta
を解く。
しかしながら、半径Rだけだと厳格すぎるので、R2に対し、データDのデータごとにu(n)の遊びを用意する。
\min_{R^2, b} \bigl\{{R^2 + C \sum_{n=1}^N} {u^{{(n)}}}\bigr\} \quad subject \quad to \quad ||x^{{(n)}} - b||^2 \leq R^2 + u^{{(n)}} \tag{6.1} \\
ただし n=1 \cdots N ,\quad ||a|| = a^Ta, \quad C:正則化定数, \quad u^{{(n)}} \geq 0
すると、この図のように、各データが収まるべき球が少し大きくなる。これがいわゆる遊びと考えられる。
(6.1)の最適化を解いた結果が、
(R^{2*},b^*, u^* )
とすると、異常度を「球からはみ出した長さ」として定義すると、
\begin{align}
a(x') &= ||x' - b||^2 - R^2 \\
&=K(x', x') - 2K(b^*, x') + K(b^*,b^*) - R^{2*} \tag{6.2} \\
\end{align} \\
K(・,・)の表記は、基本は内積でK(b,x')=bTx'だが、のちに拡張定義あり。
このように異常度が求められるので、先ほどの(6.1)の最適化問題を解きたい。しかし、複数の不等式制約がある問題は大変なので、ラグランジュ関数に変換して、解きやすい形にして問題を解く、双対問題として最適化問題を解く。
ラグランジュ乗数法
ラグランジュ乗数法とは、等式制約h(x)=0、もしくは不等式等式制約g(x)≧0の元で、関数f(x)を最大化させるために、
ラグランジュ関数L(x,λ)=f(x)+λg(x)を作って、ラグランジュ関数の最適化問題を解く方法。
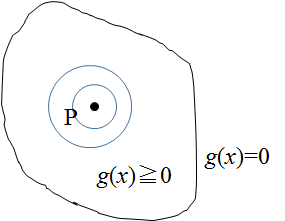
g(x)≧0の領域内にf(x)の最大値がある場合
もしf(x)の最大値を取る点Pが、g(x)≧0の領域にあれば、領域関係なくそのPのときの値が最大値になるため、制約に関係なくf(x)の最大値を求めればよい。この場合の制約は、無効制約と呼ばれる。(PRML本より)
無理やりラグランジュ関数の形に置き換えると、ラグランジュ乗数λ=0として、
L(x,\lambda) = f(x) + \lambda g(x)
となる。右辺第二項は0になるので、実質的にf(x)を最大化することになる。
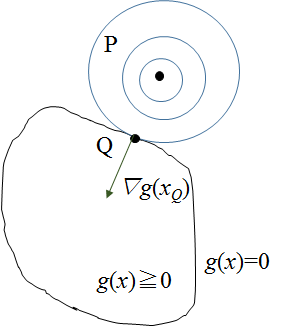
g(x)≧0の領域外にf(x)の最大値がある場合
g(x)≧0の領域外に点Pがある場合は、点Pからf(x)の等高線を引いていき、g(x)=0の制約面と接する点QでF(x)の最大値を取るはず。
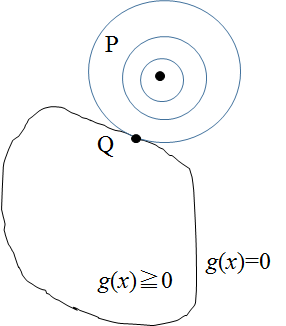
この場合の制約は、先ほどの無効制約に対して、有効制約と呼ばれる。(PRML本より)
ここで、制約式g(x)の勾配∇g(x)は、g(x)=0の制約面において、常に垂直になる。
このことは、PRML本に以下のように説明されていた。
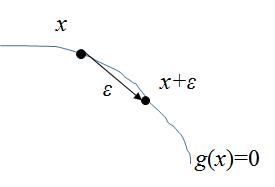
まず制約面g(x)=0上の点、x, x+εを考える。
εは微小で、互いに近傍である。ここでg(x+ε)をテーラー展開すると、
g(x+\epsilon) \simeq g(x) + {\epsilon}^T \nabla g(x)
xとx+εはg(x)=0上なので、g(x+ε) = g(x) よって
{\epsilon}^T \nabla g(x) \simeq 0
が成立。||ε||→0の極限では、
{\epsilon}^T \nabla g(x) = 0
となり、
また||ε||→0の極限では、εはg(x)=0の接線になる。すると内積の形をしているこの式は、εと∇g(x)が垂直であることを示している。
よって∇g(x)は曲面g(x)=0上で常に垂直になる。
また点Qにおいてf(x)の勾配∇f(x)も、制約面g(x)=0に垂直である必要がある。垂直でない場合は、g(x)=0上に沿って、f(x)がより大きくなる点を探せてしまう。
よって、∇g(x)と∇f(x)はお互いg(x)=0に対して垂直となり、f(x)の方向は制約面に対して外向きに、g(x)は内向きになるため、この図のようになる。
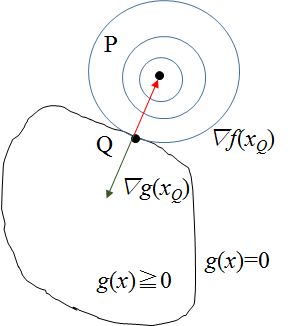
ここでラグランジュ乗数λを導入すると、この関係は
\nabla f(x_Q) = -\lambda \nabla g(x_Q) \\
ただし \lambda > 0
となる。変形させると、
\frac{\partial }{\partial x} \bigl\{ f(x) + \lambda g(x) \bigr\} = 0
ここで、偏微分の中身は、ラグランジュ関数L(x,λ)になっていることに気付く。
g(x)=0なので、結果的にλg(x)=0となる。
KKT条件
以上、g(x)=0の領域内と領域外の2通りで検証したところ、
ラグランジュ関数を最大化させると、λg(x)=0となるため、結果的にf(x)の最大化をしていることになる。
まとめると、
\max_x f(x) \quad subject \quad to \quad g(x) \geq 0 \tag{6.15} \\
の局所最適解は、ラグランジュ関数
L(x,\lambda) = f(x) + \lambda g(x) \\
に対して 次の条件を満たす
\frac{\partial }{\partial x} \bigl\{ L(x, \lambda) \bigr\} = 0 \tag{6.17} \\
g(x) \geq 0 \tag{6.18} \\
\lambda \geq 0 \tag{6.19} \\
\lambda g(x) = 0 \tag{6.20} \\
これらを、カルーシュ・キューン・タッカー条件(KKT条件)と呼ぶ。
ラグランジュ乗数法の一般化と双対問題
以上の内容を、複数の不等式制約g(x)≧0, 等式制約h(x)=0について一般化すると
f(x)の最大化問題
\max_x f(x) \quad subject \quad to \quad g_i(x) \geq 0, \quad h_j(x) =0 \tag{6.21} \\
ただし i=1 \cdots C, \quad j=1 \cdots D
において、ラグランジュ関数
L(x, \lambda, \mu) = f(x) + \sum^C_{i=1} \lambda_i g_i(x) + \sum^D_{j=1} \mu_j h_j(x) \tag{6.22}
を作る。
このとき、KKT条件(6.17)を元に、
\frac{\partial L(x, \lambda, \mu)}{\partial x} = 0 \tag{6.23}
をxについて解析的に求めると、x = u(λ, μ)のような式となる。このxをラグランジュ関数L(x,λ, μ)に代入すると、
l(\lambda, \mu) \equiv \max_x L(x, \lambda, \mu)
となる。
この式について、f(x)との関係を考えると
l(\lambda, \mu) \geq f(x) + \sum^C_{i=1} \lambda_i g_i(x) + \sum^D_{j=1} \mu_j h_j(x) \geq f(x) \tag{6.24}
が成立する。
第1項と第2項については、第2項がラグランジュ関数そのもので、それを最大化させた第1項のほうが大きいのは明らか。
第2項と第3項については、g(x)≧0とλ≧0が成立することから。
このことから、
l(\lambda, \mu) \rightarrow 最小化 \quad subject \quad to \quad \lambda_1 \cdots \lambda_C \geq 0 \tag{6.25}
を解くことで、l(λ,μ)の最小値を求めることで、f(x)の最大値を求める。
(6.21)を主問題、ラグランジュ関数に変換した新しい問題(6.25)を双対問題
と呼ぶ。
元問題に対する双対問題への適用
元問題のおさらい
もともとの問題(6.1)に対して、双対問題に変換する。(6.1)をラグランジュ乗数法の形で書き直すと、
f(x) = R^2 + C \sum_{n=1}^N} {u^{(n)}
制約が
R^2 + u^{(n)} - ||x^{(n)} - b||^2 \geq 0, \quad u^{(n)} \geq 0, \quad ただしn=1 \cdots N
となる。
ラグランジュ乗数法の最小化について
また、元々の最適化問題は、最小化であり、先に述べたラグランジュ乗数法は最大化であるので、ラグランジュ関数の作り方を少し変える。
g(x)≧0の元でf(x)を最大化したいときは、ラグランジュ関数を、
L(x, \lambda) = f(x) + \lambda g(x)
としていたが、最小化する場合は、
L(x, \lambda) = f(x) - \lambda g(x)
と、符号を変える。
ラグランジュ関数適用
制約にそれぞれ、α、βのラグランジュ乗数を導入すると、ラグランジュ関数は、
L(R^2,b,u,\alpha, \beta) \equiv R^2 + C \sum_{n=1}^N u^{(n)} - \sum^N_{n=1} \beta_n u^{(n)} - \sum^N_{n=1} \alpha_n \{
R^2 + u^{(n)} - ||x^{(n)}-b||^2 \}
双対問題の作成
KKT条件(6.17)より、R,b,uについて変微分することで最大化させ、Lをαとβだけの関数にする。
R2で微分
\frac{\partial L}{\partial R^2} = 1 - \sum^N_{n=1} \alpha_n =0 より、\tag{6.3}
\sum^N_{n=1}\alpha_n=1 \tag{6.3'}\\
bで微分
\frac{\partial L}{\partial b} = 2 \sum^N_{n=1}\alpha_n b - 2 \sum^N_{n=1}\alpha_n x^{(n)} =0 より \tag{6.4}
b \sum^N_{n=1}\alpha_n = \sum^N_{n=1}\alpha_n x^{(n)}
(6.3')を代入して
b = \sum^N_{n=1}\alpha_n x^{(n)} \tag{6.4'}
uで微分
\frac{\partial L}{\partial u^{(n)}} = C - \beta_n - \alpha_n = 0 \quad ただしn=1 \cdots N \tag{6.5}
ラグランジュ関数を整理すると、
L(R^2,b,u,\alpha, \beta) = R^2(1- \sum^N_{n=1} \alpha_n) + \sum_{n=1}^N u^{(n)}(C - \beta_n - \alpha_n)
+ \sum^N_{n=1} \alpha_n ||x^{(n)}-b||^2
(6.3')(6.4')(6.5)を代入して第一項、第二項を削除
l(\alpha, \beta) = \sum^N_{n=1} \alpha_n ||x^{(n)}-\sum^N_{n=1}\alpha_n x^{(n)}||^2
ここで内積っぽい定義Kを
K_{n,n'} = K(x^{(n)}, x^{(n')})
として展開すると、
l(\alpha, \beta) = \sum^N_{n=1}\alpha_n K_{n,n}
- 2\sum^N_{n=1} \alpha_n K(x^{(n)}, \sum^N_{n'=1}\alpha_{n'}x^{(n')})
+ \sum^N_{n=1} (\alpha_n \sum^N_{n'=1}K_{n',n'})
ここから不明・・・
結果
l(\alpha, \beta) \equiv \min_{R^2,b,u} L(R^2,b,u,\alpha, \beta) \\
= \sum^N_{n=1}\alpha_n K_{n,n} - \sum^N_{n=1,n'=1} \alpha_n \alpha_{n'} K_{n,n'} \tag{6.6}
となる。
ここで各α、βに対して非負条件がKKT条件によって与えられるが、βは(6.6)にないので、式(6.5)より
0 \leq \beta_n \leq C- \alpha_n
となる。
出来上がった双対問題
ラグランジュ乗数法によって双対問題に変換された、解くべき問題は以下の通りである。
\max_{\alpha} \bigl\{ \sum^N_{n=1}\alpha_n K_{n,n} - \sum^N_{n=1,n'=1} \alpha_n \alpha_{n'} K_{n,n'} \big \} \\
\quad subject \quad to \quad 0 \leq \alpha_n \leq C \quad (n=1\cdots N) \tag{6.8}
続きます。
サポートベクトルデータによる異常検知の続き