強化学習の一手法であるQ-learning とディープニューラルネットを組み合わせた Deep Q Network、通称DQNを使って倒立振子の振り上げ問題を解決してみます。
問題設定
「倒立振子の振り上げ問題」というのは、今回はこういう問題設定です。
まず空中に静止したモータがあって、モータ軸に棒の一端がつながっています。棒は中心に質量が集中していて剛性$\infty$で太さ0の、よくある棒です。初期状態では棒は重力にしたがって下向きにぶら下がっています。この状態から振り子を振り上げて倒立状態で静止させてください、という問題です。古きよき制御工学では、振り上げ用と静止用に別設計されたコントローラを2つ用意して切り替えるなど、非線形要素を含むコントローラを用いて対処することになります。いや、やったことないですけど、そうらしいです。
今回は、モータは右か左に一定トルクの回転しかできない、とします。また、ちょっとしたいじわるですが、モータのトルクはさほど大きくなく、初期状態から一方向に回し続けても重力に勝てず振り上げはできない、という条件にしました。下記はその罠にハマっているときのアニメーションです。ずっと右にトルクをかけている状態ですが、水平に向かうほど重力加速度の角度方向への寄与が大きくなるので押し戻され、振動します。
DQNそのものについてはこちらの素晴らしい記事が詳しいので、主に結果と、実装まわりの工夫を今回の記事では説明します。
まず結果から
エージェント(今回はモータのコントローラ)は環境(モータと棒)に対してアクション(モータの回転方向の指示)を行い、報酬と何らかの観測結果を得る、という条件下でエージェントに最適方策を学ばせます。
報酬は、モータから見た棒の先端の高さを$h$としたとき、高いほどうれしい、という下記のような関数$r(h)$を用いました。
r(h)= \Biggl\{\quad
\begin{eqnarray}
5h & \mathrm{if} h\ge 0\\
h & \mathrm{if} h< 0
\end{eqnarray}
プラス側にバイアスをかけたのですが、余計なお世話だったかもしれません。観測は、ATARIの例などでは画面の画像を直接入力していますが、今回は振り子の角度そのものを入力してみました。シミュレーションの4ステップぶんの角度列をシーケンスとして得られることとします。
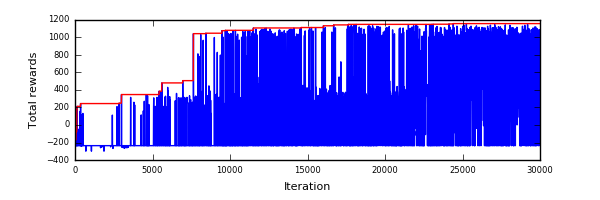
下記が成長の様子をプロットしたものです。横軸が試行回数、縦軸が試行で得られた総得点です。青点が各世代の結果、赤線がハイスコアです。
非線形性と多峰性を持った系のせいか、結果はとっても振動的で、収束後にも正負の成績で振動していますが、ハイスコア結果は確実に成長しています。以下で成長の過程を見てみます。
120回目、往復すれば振り上げが可能だということに気づきますが、その後止めることができません。

6950回目、振り上げ後の静止のコツをつかんできたようです。もうちょっとだ!がんばれー!

30000イテレーション内のベスト結果がこれです。ち
ょっと行き過ぎてますが、最初の振り上げを最短時間でやるほうが有利と気づいたようです。
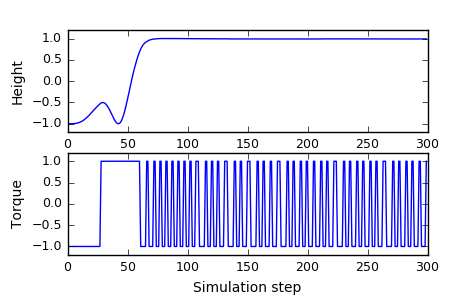
思ってたよりうまくいってちょっと驚いています。最後の例について、時系列で高さとモータへの制御入力のプロファイルをプロットしたのが以下です。振り上げ動作と保持では考え方が全く違うのですが、そのことを学べている様子がわかります。
DQNの実装について
先ほど紹介したDQNの記事には実装も示されているのですが、今回は理解のために車輪の再実装をしてみました。こちらの論文にしたがって実装したものをこちらに置きました。
論文を読んだだけでは十分理解できていなかったのは、肝心のディープネットはどのように構成するのか、どのように更新するのか、というところでした。その辺りを解説します。
ディープニューラルネット$Q$は状態観測結果のシーケンスを入力すると、各行動の行動価値を出力するネットです。行動価値は、今回の場合は「入力された角度シーケンスの示す状況では、モータを右、左に回すのはそれぞれ、どれぐらいうれしいか」ということを示すベクタになります。
もちろん学習初期ではこのネットはランダムなので、でたらめな結果を返します。これを今から説明する手順で更新していくと、将来にわたってトータルの報酬がたくさん得られるようないいかんじのネットに成長していきます。
状態$s_t$に対してあるアクション$a_t$ を行って報酬$r_t$が得られ、$s_{t+1}$に変わったとします。このとき、$s_t$を入力したときの$Q$の出力である行動価値ベクタ$Q(s_t)$のうち、$a_t$に相当する行動価値だけを下記の式にしたがって書き換えた$y_t$を作ります(だいぶ元論文から記号を変えています)。
y_t = Q(s_t) \\
y_t[a_t] \leftarrow r_t + γ max Q(s_{t+1})
この$y_t$に$Q(s_t)$が近づくように、ネットの重みを一歩更新します。今回の報酬と、次の一手で得られる最大の行動価値に一定の割引率$\gamma$ をかけたものを足しています。エピソード終端までの行動価値を足した和から、今回の行動の価値を決めるのが理想ですが、演算時間的にも無理があるので、次の一歩だけを行います。この更新手順を無限回繰り返せば、状態から総報酬に基づいた行動価値を得られることになります。ほんとかしら。少なくとも私はそう理解しました、ぐらいの表現にしておきます。
ディープネットそのものの構成はあまり試行錯誤をしていませんが、深めにしておいて間違いはないのかなと思います。ほんとうはDropoutやBatch Normalizationなどを入れて汎化性能をあげたほうがよいのでしょうか。問題によるとは思いますが。
Best Experience Replay
今回の実装は基本的には論文通りですが、一点だけ工夫した点があるので解説します。
学習に使う「状態・アクション・報酬」のセットは、お互いに相関のないものを使ったほうがよいそうです。このためにER(Experience Replay)という手法が重要になります。DQNの最大のポイントの一つのようですね。過去の経験を覚えておいて、そこからランダムで先ほどのセットを取り出したものに対して学習を行う、という手法です。
一回の試行のことをエピソードと呼びますが、元論文ではすべてのエピソードをまるごと記憶します。あたらしい経験を得るために、各エピソードでは $\epsilon$-greedyと呼ばれる方法でいろいろと試します。一定確率$\epsilon$でランダム動作とネットにしたがった動作(greedy動作)を選択するのが$\epsilon$-greedyです。学習初期は$\epsilon$が大きく、ほとんどランダム動作だけから学ぶことになります。
学習が十分に進んだあとは、greedy動作だけで結果を出すことができます。このため、ときどき完全greedy動作をしてみて様子を見ます。
DQNの論文で常々疑問だったのですが試してみるとやはりその通りで、初期は特に、あきらかに覚える価値のないエピソードがどんどん溜まっていき、数少ない良い経験はメモリから消えていきます。なにせ完全ランダムですから。もちろん失敗例から学べることもあるでしょうが、どうせならちょっとでもいい経験を手本にしたほうがよいのではないかと思います。というわけで今回は、$\epsilon$-greedyエピソードもgreedyエピソードも区別せず、良い点数(生涯報酬)を得たエピソードを優先して記憶に残すことにしました。歴代ベスト100エピソード、を保持することにして、ランキング内に入る点数のエピソードだけ記憶入りします。ただし、ランキングに入れなくても1%の確率で記憶入りできます。
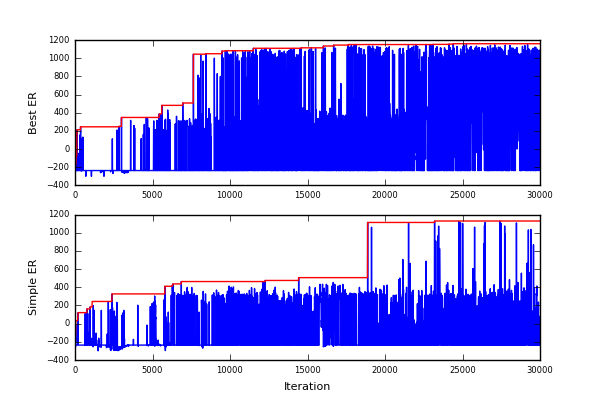
この方法を仮にBest ERと呼ぶことにします。同じシード値で初期化した状態から、Best ERとシンプルなERとの収束状況の違いをプロットしてみました。
だいぶ効果あるように見えます。計算機資源の都合からいろんなケースでは試してませんが。。
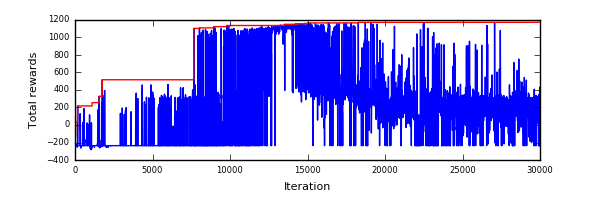
新しい経験をまったく取り入れない方式をしばらく試したのですが、収束後、しばらく黄金時代を迎えたあとに衰退していくことがわかりました。下記のようになりました。
乱数のseedを変えても同じようなことが起きました。原因はよく調べていませんが想像するに、成長したgreedyエピソードの高得点な実績がランキングを埋め尽くしたあとの出来事なので、データの相関がありすぎたり多様性を失ったりしているためではないかと思います。ただ、改善版は黄金時代にも至っていないだけにも見えますのでまだ改良の余地があるかなとも思います。
また、Best ERは小さな成功にとらわれすぎてハマる場合があると思います。あとは環境の変化にも十分対応できませんね。過去の栄光にとらわれてしまうので。なんだか先ほどの黄金時代の件といい、つい人生論に重ねたくなってしまいますが、まあ、タスクによる、ということですね。
DQNというものの傾向なのかもしれませんが、学習が進んでるかどうかがわかりにくいので、良さそうな候補はセーブ、というのは必須ですね。また、多峰性関数の数値最適化にありがちなことですが、成果が出るまでの時間が初期値にすごく依存するなあというのが印象です。とはいえ、今回のケースを何回か試した感じだと1万イテレーション付近でほぼ最高スコアを叩き出せます。手元のPC(MacBook Pro Core i5 2.5GHz x2Core)で1時間ぐらいでした。
まとめ
常々やってみたかったDQNを試すことができました。また、収束を早める方法としてBest ERという方法を提案してみました。自分で実装すると理解が深まって良いですね。
コントローラ側のチューニングも切り替えも行わず、こういう結果が出るのは驚きです。モータ制御量を連続量にする、二重振り子化、観測を角度ではなく画像でやる、実機とウェブカメラでやる、などなど、やりたいことはいろいろ出てきますが時間の都合でここまでとします。
今回はCPUでやりましたが、やはりこの分野で試行錯誤するにはCPUでは限界ですね。先日発表されたCloud Machine Learningが楽しみです。おとなしくGPUを買えよという声も聞こえますが。。。