数学が苦手な人のためのNumPy用例集

NumPyは、科学技術計算を行う、特に行列や多次元配列の計算をするのに便利なPython用の拡張モジュールです。

ですが、数学を使わなくても、NumPyは便利です。
特に、[ [1,2],[3,4],[5,6] ]のような多重リストを使う代わりに、NumPyの配列を使った方が便利な場合があります。

今回は、NumPyの主に配列の使い方について、用例を挙げて紹介したいと思います。

はじめに

NumPyは、数学向けのライブラリーではありますが、NumPyの配列は、数学とは関係なく便利に使える部分もあります。
とは言え、ウェブ上のサンプルは数学で使う人のものが多いですし、数学以外で具体的にどう使うのかは分かりにくいのではないかと思いました。

そこで、数学とはほとんど関係ない使い方をいくつか例示して、NumPyの（主に配列の）便利さを紹介するのがこの記事の目的です。

私も数学は得意ではないですし、使っていないのでほとんど分からないレベルです。

もちろん、プログラミングは少なからず数学に関係しているので、全く使わないという意味ではありません。
ここで言っている数学とは、行列とか微分積分などで使う数式をプログラミングで表現するような使い方のことを指しています。

内容の一部に数学っぽいものが少しだけ含まれていますが、そこは分からなくても本題には関係ないので気にしないで読み進めてください。

使用上の注意

ここで取り上げている用例は、データ操作を学ぶためのヒントを提供するものであり、必ずしも取り上げているコードが効率の良い処理とは限りません。

実際に運用で使用する際には、必ずご自身で検証してからにして下さい。

対象となる読者

NumPyを使ったことがないPythonユーザー。
特に、数学が苦手でNumPyを敬遠している方や、数学と無縁でNumPyを使っていない方が対象です。

実行環境

OS・処理系など

動作を確認した環境は、主にこれ↓です。

• Python 3.5.2 | Anaconda 4.1.1 (64-bit)
• Windows 7 64bit

全部は確認していませんが、特にOS依存のものは扱っていません。
結果は主に対話環境のものを掲載していますが、Jupyter Notebookを使っている箇所もあります。

使用しているモジュール・ツール

下記のうち、標準モジュールはcalendarだけです。

モジュール名	バージョン	説明
NumPy	1.11.1	今回の主役となる数値計算ライブラリーモジュール
calendar	(3.5.2)	テキストカレンダーを扱うための標準モジュール
PIL	1.1.7	画像処理モジュール
Matplotlib	1.5.1	グラフをプロットするモジュール 今回は画像表示で使用
Jupyter Notebook	4.2.1	Webブラウザー上で使えるREPL

※ Jupyter Notebookのバージョンは、Notebook Serverのもの

基礎知識

NumPyモジュールnumpyを使うには、別名npを使うのが一般的です。
公式リファレンスでもそうなっています。

import numpy as np

この記事でもそれに倣います。
本文中では、このインポートが無い場合でも、常にインポート済みのものとして読んでください。

NumPyの配列は、numpy.ndarray（以降、本文中では"NumPyの配列"と表記）という型になります。

>>> np.array([1, 2])
array([1, 2])
>>> type(np.array([1, 2]))
<class 'numpy.ndarray'>

これは標準のリストと一見似ていますが、NumPyの配列はそれと比べて非常に豊富な操作が可能です。
標準のリストとの性質の違いについては、下記リンクの記事を参照してください。

NumPy 配列の基礎 — 機械学習の Python との出会い
http://www.kamishima.net/mlmpyja/nbayes1/ndarray.html

テキストカレンダー - 1次元配列から2次元への変換

テキストカレンダーとは、コンソール上にテキストでカレンダーを表示するものを指します。
Unix-like環境のcalコマンドで出力されるのもテキストカレンダーです。

実は、Pythonの標準モジュールには「テキストカレンダー」そのものを扱うモジュールcalendarがあります。

calendar – 日付の処理 - Python Module of the Week
http://ja.pymotw.com/2/calendar/

なので、わざわざイチから作る必要はありませんが、NumPyを使う例として分かりやすい題材だったので、取り上げてみました。

この項では、calendarモジュールをほぼ使わずに処理する方法について考えてみます。
「ほぼ」と書いたのは、テキストカレンダーを作るには月初日と月末日を求める計算が必要になりますが、その計算について考えるのは今回の目的ではないので、それを求めるのにcalendarモジュールのmonthrange()関数を使うからです。

処理イメージ

それでは本題に入ります。

実物のカレンダーを見ていただくと分かると思いますが、テキストカレンダーは7x6の固定サイズの2次元表に適切な値を当てはめていけば、9割9分完成です。
とはいえ、最初から2次元だと処理が面倒な気がします。データを作るところは1次元配列で行い、後で2次元に変換するのが良さそうです。

NumPyの配列には、N次元の配列を任意の次元に変換する、reshape()メソッドがあります。
これを使えば、1次元配列を2次元に変換できます。

おおざっぱに書くと、下記のような流れで処理をすればOKでしょう。

・先頭の空データ（1次元）
・1〜31（1次元）
・末尾の空データ（1次元）
   ↓ 結合
・先頭の空データ＋1〜31＋末尾の空データ（1次元） ※サイズは42
   ↓ 2次元に変換(reshape)
・先頭の空データ＋1〜31＋末尾の空データ（2次元）
   ↓ 各要素を文字列に変換
・カレンダーデータ（2次元）

1次元のデータを生成

まず、calendar.monthrange()関数で、必要な数値を求めます。

>>> import calendar
>>>
>>> w, c = calendar.monthrange(2016, 7)
>>> w # 月初日の曜日
4
>>> c # 月の日数
31

月初日の曜日は、月曜日始まりの曜日が返されます。つまり、月曜日が0で日曜日が6になります。
今回は日曜日始まりのカレンダーを作りたいので、補正しておきます。

# （続き）

>>> w = w + 1 if w < 6 else 0
>>> w
5

ゼロがセットされた配列を作るには、np.zeros()関数を使います。
数字の並びで配列を作るには、標準のrange()関数と似たnp.arange()関数を使います。

dtypeを指定しない場合、デフォルトのデータ型はfloat64となります。

# （続き）

>>> np.zeros(1).dtype
dtype('float64')
>>> np.zeros(1, dtype=int).dtype
dtype('int32')
>>> np.zeros(w, dtype=int)
array([0, 0, 0, 0, 0])
>>> np.arange(start=1, stop=c+1, dtype=int)
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16, 17,
       18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31])
>>> np.zeros(42 - w - c, dtype=int)
array([0, 0, 0, 0, 0, 0])

np.concatenate()関数で、配列を結合できます。
2つのNumPy配列を+で計算してしまうと、ベクトル・行列計算になってしまいますので、ご注意ください。

# （続き）

>>> np.array([1, 2]) + np.array([3, 4])
array([4, 6]) # ベクトルとしての和
>>> headfiller = np.zeros(w, dtype=int)
>>> days = np.arange(start=1, stop=c+1, dtype=int)
>>> tailfiller = np.zeros(42 - w - c, dtype=int)
>>> np.concatenate((headfiller, days, tailfiller))
array([ 0,  0,  0,  0,  0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,
       13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29,
       30, 31,  0,  0,  0,  0,  0,  0])

最初に42個のゼロを用意して、それに日の並びを上書きする方法も考えられます。
この場合、上書きする配列のサイズと範囲のサイズが合っていないとエラーになりますので注意してください。

# （続き）

>>> days = np.zeros(42, dtype=int)
>>> days[w:w+c] = np.arange(start=1, stop=c+1, dtype=int)
>>> days
array([ 0,  0,  0,  0,  0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,
       13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29,
       30, 31,  0,  0,  0,  0,  0,  0])

標準のリストから生成するほうが分かりやすければ、np.array()関数で後からNumPy配列に変換します。
dtypeは元のリストの型が維持されます。

# （続き）

>>> days = np.array([0] * w + list(range(1, c+1)) + [0] * (42 - w - c))
>>> days.dtype
dtype('int32')
>>> days
array([ 0,  0,  0,  0,  0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12,
       13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29,
       30, 31,  0,  0,  0,  0,  0,  0])

これで1次元配列のカレンダーができました。

1次元配列を2次元配列に変換

次に、これを2次元配列に変換します。
次元の指定は、行・列の順番なので、(6, 7)になります。

# （続き）

>>> days.reshape((6, 7))
array([[ 0,  0,  0,  0,  0,  1,  2],
       [ 3,  4,  5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14, 15, 16],
       [17, 18, 19, 20, 21, 22, 23],
       [24, 25, 26, 27, 28, 29, 30],
       [31,  0,  0,  0,  0,  0,  0]])

あとは、数値を文字列表現に変換すれば、データは完成です。

各要素を文字列表現に変換

リストの各要素を変換した新しいリストを作るには、標準関数ではmap()関数やリスト内包表記を使います。
NumPyの配列で同じようなことをするには、np.vectorize()関数を使います。

# （続き）

>>> mapper = np.vectorize(lambda x: "  " if x == 0 else "%2d" % x)
>>> mapper
<numpy.lib.function_base.vectorize object at 0x0000000002D3C668>
>>> mapper(days.reshape((6, 7)))
array([['  ', '  ', '  ', '  ', '  ', ' 1', ' 2'],
       [' 3', ' 4', ' 5', ' 6', ' 7', ' 8', ' 9'],
       ['10', '11', '12', '13', '14', '15', '16'],
       ['17', '18', '19', '20', '21', '22', '23'],
       ['24', '25', '26', '27', '28', '29', '30'],
       ['31', '  ', '  ', '  ', '  ', '  ', '  ']],
      dtype='<U2')

vectorizeで生成された関数オブジェクトは、map()関数に変換関数を部分適用したようなものになります。
この関数オブジェクトに配列を適用すると、mapされた配列が返されます。

このマッピングとreshapeの処理順序は逆でもかまいません。

あとは、結合して出力するだけです。
装飾はお好きなように。

# （続き）

>>> strdays2d = mapper(days.reshape((6, 7)))
>>> print("\n".join([" ".join(x) for x in strdays2d]))
                1  2
 3  4  5  6  7  8  9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
31

完成版

最後に、関数にまとめたものを掲載します。

• テキストカレンダーのPythonコード

import numpy as np
import calendar

def print_calendar(y, m):
    w, c = calendar.monthrange(y, m)
    w = w + 1 if w < 6 else 0
    # ゼロ配列ではさむバージョン
    headfiller = np.zeros(w, dtype=int)
    tailfiller = np.zeros(42 - w - c, dtype=int)
    days = np.concatenate((headfiller, np.arange(start=1, stop=c+1, dtype=int), tailfiller))
    # 最初にゼロを作るバージョン
    # days = np.zeros(42, dtype=int)
    # days[w:w+c] = np.arange(start=1, stop=c+1, dtype=int)
    # 標準リストから作るバージョン
    # days = np.array([0] * w + list(range(1, c+1)) + [0] * (42 - w - c))
    mapper = np.vectorize(lambda x: "  " if x == 0 else "%2d" % x)
    strdays2d = mapper(days).reshape((6, 7))
    print("%d %d" % (y, m))
    print()
    print("\n".join([" ".join(x) for x in strdays2d]))

if __name__ == "__main__":
    print_calendar(2016, 8)

• 実行結果

2016 8

    1  2  3  4  5  6
 7  8  9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31

ビットマップ - 2次元＋1次元の配列から画像を生成

画像を表現するビットマップは、XY座標の2次元配列と、各ピクセルの色を表す情報で構成されます。
これを、NumPyの2次元配列で表現してみましょう。

今回使用するモジュールは、色をサイズ3の配列（[R, G, B]）で表すので、それを合わせて3次元で表現します。
ライブラリーによっては、色名または#rrggbb形式で指定するものがありますので、その場合はintかstrの2次元配列で表現することになります。

画像の処理についてはPILモジュールの機能は豊富なので、本格的に画像の処理を行う場合は、そちらの機能を駆使して下さい。

PILで画像を生成

PILでNumPyの配列から画像を生成するには、次のようにします。

import numpy as np
from PIL import Image

imgdata = np.zeros((16, 16, 3), dtype=np.uint8)
imgdata[:] = [255, 0, 0]

im = Image.fromarray(imgdata)
im.show() # WindowsではイメージビューアーでBMPファイルとして表示された
im.save("/path/to/image.png", "PNG")

imgdata[:] = ...とすることで、2次元のすべての要素に同じ値を代入することができます。（3次元の、ではないところがポイント。）

Image.fromarray()関数で、画像オブジェクトを生成します。
show()メソッドを実行すると、OSのイメージビューアーなどで表示されます。
save()メソッドを実行すると、画像をファイルに保存できます。

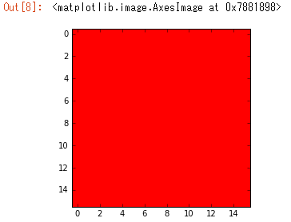
このコードを実行すると、16x16の赤で塗りつぶされたPNG画像ファイルが生成されます。

Jupyter Notebook上でMatplotlibで描画

もっと手軽な方法として、Matplotlibを使ったものがあります。
Jupyter Notebook上で、直接生成した画像を表示するには、次のコードを実行します。
データはPILのときと同じです。

%matplotlib inline

import matplotlib.pyplot as plt
import numpy as np

imgdata = np.zeros((16, 16, 3), dtype=np.uint8)
imgdata[:] = [255, 0, 0]

# plt.figure(figsize = (1.75, 1.75)) # サイズが100x100の場合にほぼ原寸
# plt.axis("off") # 目盛りを表示しない
plt.imshow(imgdata)
# plt.show() # オブジェクトの文字列表現を消す

この方法は、デフォルトでは画像のサイズが自動的に拡縮されてしまいます。
また、グラフとして表示されるので、メモリが表示されます。
コード例のコメントアウトしている箇所のコードを使えば、サイズを調整したり、画像だけを表示したりできます。

これ以降の例ではこの設定は冗長なので、imshow()関数だけを使っています。

• 実行結果

※画像は縮小しています。（以下同様。）

これ以降は、Jupyter Notebookで実行したものを掲載していますので、Jupyter Notebookを使わない場合は、PILでファイル出力するコードに読み替えてください。

ループで処理

ここでは、ビットマップの操作を通して、NumPyの多次元配列を操作する方法について見ていきます。

100x100の画像を作ってみましょう。
そして、緑をx,yの数値に対応させて、値を変化させてみます。

NumPyの配列は、imgdata[y, x]のように多次元配列を自然に扱えるようになっています。
注意すべきなのが、2次元配列へのアクセスは、1次元目が縦方向、2次元目が横方向を意味するので、[y, x]となる点です。

次の例は、ループで各要素に色情報をセットする処理です。
xとyの値を使って緑の値だけを変化させています。

%matplotlib inline

from matplotlib.pyplot import imshow
import numpy as np

w, h = 100, 100 # 幅・高さ
imgdata = np.zeros((w, h, 3), dtype=np.uint8)
for x, y in [(x, y) for x in range(w) for y in range(h)]:
    imgdata[y, x] = [0, x + y, 0]

imshow(imgdata)

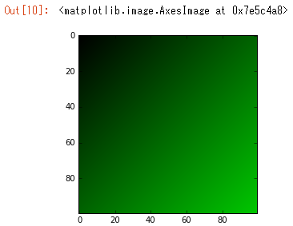
• 実行結果

緑のグラデーションが描画できました。

範囲で処理

範囲を指定して、そこに同じ値をセットすることもできます。
[10:30, 50:80]とすることで、(50, 10),(50, 30),(80, 30),(80, 10)を頂点とする長方形の範囲の要素をすべて指定することができます。

%matplotlib inline

from matplotlib.pyplot import imshow
import numpy as np

w, h = 100, 100
imgdata = np.zeros((w, h, 3), dtype=np.uint8)
imgdata[10:30, 50:80] = [0, 0, 255]

imshow(imgdata)

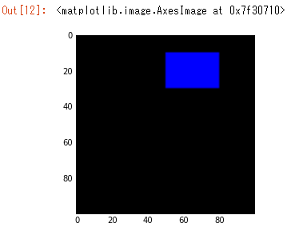
• 実行結果

バリエーション

これらを組み合わせて、模様や図形を描画することができます。

次のコードは、ループの処理と範囲の処理を組み合わせて画像を描画する例です。
※sin関数、cos関数は、周期的な値を得るためのもので、ここでは数学の知識は関係ないので、難しく考えなくて良いです。

• 模様と長方形数個を描画するPythonコード例

%matplotlib inline

from matplotlib.pyplot import imshow
import numpy as np
from math import sin, cos

w, h = 100, 100
a = np.zeros((w, h, 3), dtype=np.uint8)
for x, y in [(x, y) for x in range(w) for y in range(h)]:
    v = int(127 + sin(x * 0.6) * cos(y * 0.6) * 128)
    a[y, x] = [v, v, 0]
a[10:30, 10:70] = [int("ff", 16), int("66", 16), 0]
a[20:50, 20:80] = [int("ff", 16), int("cc", 16), 0]
a[30:70, 30:90] = [int("66", 16), int("ff", 16), 0]

imshow(a)

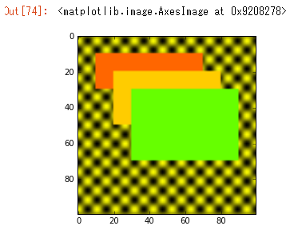
• 実行結果

数独 - 行や列などのスライス（部分配列）の取り出し

数独、またはナンバープレイスとは、数字パズルの一種です。
9x9の表に、縦・横・3x3に同じ数字が入らないように1〜9の数字を埋めていくパズルです。

数独 - Wikipedia
https://ja.wikipedia.org/wiki/%E6%95%B0%E7%8B%AC

NumPyの2次元配列を使って、数独を解くプログラムを作ってみましょう。
ここではごく単純なロジックしか扱いませんので、数独を知らなくても大丈夫です。

数字を埋めるためのもっとも単純なロジックは、あるマスから見て、縦・横・3x3に使われていない数字を探すことです。
縦の数字リスト、横の数字リスト、3x3の数字リストを取り出すのに、NumPyの配列が便利です。
ただし、NumPyの配列だけでは少し面倒な操作もありますので、標準のコレクション型と組み合わせて使います。

問題のサンプルデータとして、下記の2次元配列を使います。
ゼロは埋まっていないマスを示します。

grid = np.array([
[3, 0, 0, 0, 0, 9, 0, 0, 8],
[0, 0, 0, 0, 0, 6, 7, 0, 0],
[9, 8, 2, 0, 0, 0, 6, 0, 0],
[0, 9, 0, 0, 3, 0, 4, 0, 0],
[0, 3, 5, 0, 0, 0, 2, 1, 0],
[0, 0, 7, 0, 2, 0, 0, 9, 0],
[0, 0, 4, 0, 0, 0, 9, 7, 5],
[0, 0, 9, 6, 0, 0, 0, 0, 0],
[8, 0, 0, 4, 0, 0, 0, 0, 2],
])

スライス（部分配列）を取り出す

9x9を標準の多重リストで表現した場合、行のリストはともかくとして、列のリストや3x3のリストを取り出すのは大変です。

NumPyでは、2次元の表としての操作が簡単にできるようになっています。

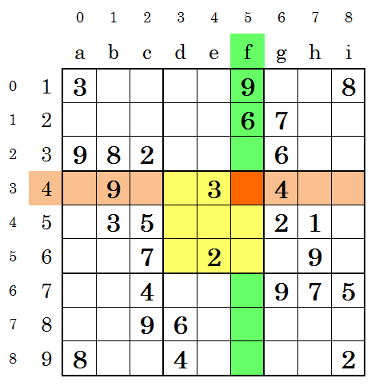
説明を分かりやすくするために、数独の問題に番号と色を付けた画像を用意しました。

この画像を参考にして、f4のマスについて調べてみましょう。

fの列（緑）の配列、4の行（ベージュ）の配列、d4-f6の3x3（黄色）の配列を取り出します。
3x3は2次元配列として取り出されますので、reshape()メソッドを使って1次元に変換します。

取り出した配列は、扱いやすくするためにlistに変換します。

ビットマップの項でも触れましたが、2次元配列へのアクセスは、1次元目が縦方向、2次元目が横方向を意味します。
つまり[x, y]ではなく、[y, x]ですので注意して下さい。

grid[:, 5],grid[3, :],grid[3:6, 3:6]のようにすることで、スライス（部分配列）を取得することができます。
同じ範囲指定を代入式で使えば、ビットマップの項で示した通り、その範囲すべてに代入できます。

# （続き）

>>> list(grid[:, 5]) # 列f: x=5の列
[9, 6, 0, 0, 0, 0, 0, 0, 0]
>>> list(grid[3, :]) # 行4: y=3の行
[0, 9, 0, 0, 3, 0, 4, 0, 0]
>>> list(grid[3:6, 3:6].reshape(9)) # d4-f6
[0, 3, 0, 0, 0, 0, 0, 2, 0]

数字リストを集計

ここからはNumPy配列を使わないで処理していきます。

列のリスト、行のリスト、3x3のリストが取得出来たら、それらを結合してからset型に変換すれば、すでに使われている数字のユニークなリストが得られます。

# （続き）

>>> used_nums = set(list(grid[:, 5]) + list(grid[3, :]) + list(grid[3:6, 3:6].reshape(9)))
>>> used_nums
{0, 2, 3, 4, 6, 9}

ゼロが不要ですが、あっても問題ないので、そのままにします。
used_nums - {0}とすればゼロを取り除くことができます。

1〜9の数列からすでに使われている数字を取り除けば、候補となる数字が残ります。
set型の-演算を使って、使われている数字を取り除きます。

# （続き）

# range(1, 10)は1～9の数字
>>> unused_nums = set(range(1, 10)) - used_nums
>>> unused_nums
{8, 1, 5, 7}

使われていない数字が1つだけなら、それがそのマスの数字に決定します。
f4は、今の状態では1つに絞れませんでした。

同様にc2について調べてみましょう。

# （続き）

>>> col = list(grid[:, 2]) # 列c: x=2の列
>>> row = list(grid[1, :]) # 行2: y=1の行
>>> sq = list(grid[0:3, 0:3].reshape(9)) # a1-c3
>>> col, row, sq
([0, 0, 2, 0, 5, 7, 4, 9, 0], [0, 0, 0, 0, 0, 6, 7, 0, 0], [3, 0, 0, 0, 0, 0, 9, 8, 2])
>>> used_nums = set(col + row + sq)
>>> used_nums
{0, 2, 3, 4, 5, 6, 7, 8, 9}
>>> unused_nums = set(range(1, 10)) - used_nums
>>> unused_nums
{1}

今度は、数字が1だけに絞れました。
ということで、c2には1が入ることが確定しました。

完成版（発展途上）

ここまでのロジックを、まだ埋まっていないマスに繰り返し適用していけば、とりあえず数独を解くプログラムの完成です。

ただし、1周の間にひとつのマスも埋めることができなければ、ギブアップとなります。
今のままでは、基本中の基本のロジックしか実装していませんので、よほど簡単な問題でなければ解けないでしょう。

完成例のコードを掲載します。

• 数独を解くPythonコード例（簡単な問題しか解けないバージョン）

import numpy as np

grid = np.array([
[3, 0, 0, 0, 0, 9, 0, 0, 8],
[0, 0, 0, 0, 0, 6, 7, 0, 0],
[9, 8, 2, 0, 0, 0, 6, 0, 0],
[0, 9, 0, 0, 3, 0, 4, 0, 0],
[0, 3, 5, 0, 0, 0, 2, 1, 0],
[0, 0, 7, 0, 2, 0, 0, 9, 0],
[0, 0, 4, 0, 0, 0, 9, 7, 5],
[0, 0, 9, 6, 0, 0, 0, 0, 0],
[8, 0, 0, 4, 0, 0, 0, 0, 2]])

nums = set(range(1, 10)) # 1～9
square_table = [0, 0, 0, 3, 3, 3, 6, 6, 6]

def fill(x, y):
    if (grid[y, x] != 0):
        return 0
    list1 = list(grid[:, x]) # 縦
    list2 = list(grid[y, :]) # 横
    xx, yy = square_table[x], square_table[y]
    list3 = list(grid[yy:yy+3, xx:xx+3].reshape(9)) # 3x3
    used_nums = set(list1 + list2 + list3)
    unused_nums = nums - used_nums
    if len(unused_nums) == 1:
        grid[y, x] = list(unused_nums)[0]
        return 1
    else:
        return 0

if __name__ == "__main__":
    for i in range(81):
        print("loop:", i + 1)
        filled = sum([fill(x, y) for x in range(9) for y in range(9)])
        if len(grid[grid == 0]) == 0:
            print("solved!")
            break
        if filled == 0:
            print("give up...")
            break
    print(grid)

このコードについて少し補足します。

filled = sum(...)のところは、ループの代わりにリスト内包表記をつかっています。
それぞれのfill()関数の呼び出し結果をsumすることで、その周回に埋めたマスの数を計算しています。

grid[grid == 0]はNumPy配列の便利な機能のひとつで、条件に一致する要素をまとめて取り出すことができます。
ここではgrid == 0としているので、ゼロの要素をすべて取り出しています。
この要素数を数えれば、埋まっていないマスの数が分かります。
これを使って、問題が解けたかどうかをチェックしています。

3x3の範囲を計算するために、変換テーブルsquare_tableを使用しています。
四則演算でもできますが、この場合はこちらの方が明快だと思います。

• 処理結果

loop: 1
loop: 2
loop: 3
loop: 4
give up...
[[3 0 6 0 0 9 5 0 8]
 [0 0 1 0 0 6 7 0 0]
 [9 8 2 0 0 0 6 0 0]
 [0 9 8 0 3 0 4 5 0]
 [0 3 5 0 0 0 2 1 0]
 [0 0 7 0 2 0 0 9 0]
 [0 0 4 0 0 0 9 7 5]
 [0 0 9 6 0 0 0 0 0]
 [8 0 3 4 0 0 1 6 2]]

最初に挙げた問題は、このロジックだけでは解けませんでした。
興味がある方は、より高度な問題が解決できるように、ロジックの追加・改造に挑戦してみて下さい。

ちなみに、Wikipediaに掲載されている最初の例題は、このロジックだけでも解けました。

おわりに

このように、処理によっては、標準のリストより格段に柔軟な操作ができます。
NumPyには他にもたくさんの機能がありますが、ここに挙げたものだけでもかなり便利なはずです。

数学に縁がない方も、まだNumPyを使ったことがない方も、ぜひNumPyを活用してみて下さい。

参考資料

Overview — NumPy v1.11 Manual
http://docs.scipy.org/doc/numpy/index.html

100 numpy exercises
http://www.labri.fr/perso/nrougier/teaching/numpy.100/

python - How do I convert a numpy array to (and display) an image? - Stack Overflow
http://stackoverflow.com/questions/2659312/how-do-i-convert-a-numpy-array-to-and-display-an-image