社会の実際の問題にデータ分析を適用してみるシリーズ。
株価の変動の分布は正規分布で考えるとよい、と大抵の投資の本に書いてありますが、本当にそうかどうか確かめてみます。と、言いますか正規分布を仮定していたLTCMが破綻したことから株価の変動は正規分布ではないよ、と投資の本にも書かれ始めてますが未だに正規分布としている本が多いところ。せっかくデータ分析を出来るようになったのだから、そういうごにょごにょしたところを、自分で試してみようとのこと。
今回はTOPIX(日次終値、2010-2016、前日との変動率)を扱い、データは http://k-db.com/ のものを使わせていただきました。
TOPIX2016<-read.csv('http://k-db.com/indices/I102/1d/2016?download=csv')
TOPIX2015<-read.csv('http://k-db.com/indices/I102/1d/2015?download=csv')
TOPIX2014<-read.csv('http://k-db.com/indices/I102/1d/2014?download=csv')
TOPIX2013<-read.csv('http://k-db.com/indices/I102/1d/2013?download=csv')
TOPIX2012<-read.csv('http://k-db.com/indices/I102/1d/2012?download=csv')
TOPIX2011<-read.csv('http://k-db.com/indices/I102/1d/2011?download=csv')
TOPIX2010<-read.csv('http://k-db.com/indices/I102/1d/2010?download=csv')
TOPIX<-rbind(TOPIX2016, TOPIX2015, TOPIX2014, TOPIX2013, TOPIX2012, TOPIX2011, TOPIX2010)
# 終値の前日との変動率
diff<-diff(TOPIX[, 5]) / TOPIX[-1, 5]
# c.f. http://kasumiko.hatenablog.jp/entry/2015/01/27/042051
# c.f. http://qiita.com/HirofumiYashima/items/69c08eba285cc278a5b5
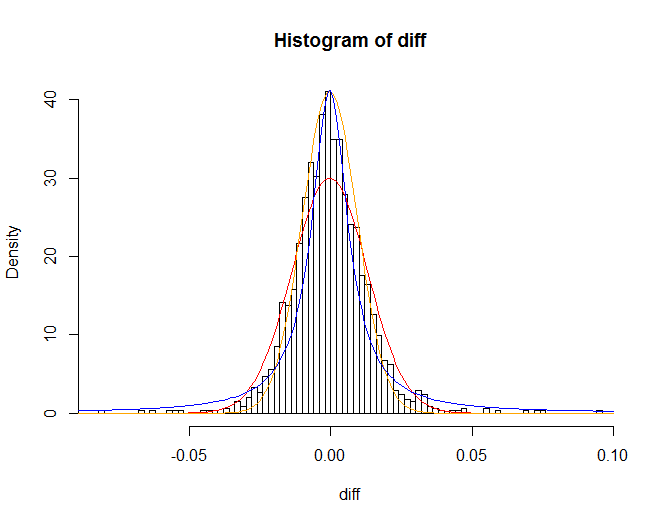
hist(diff, breaks = 100, freq = F)
lines(seq(-0.1, 0.1, 0.001), dnorm(seq(-0.1, 0.1, 0.001), mean = mean(diff), sd = sd(diff)), col = 'red')
lines(seq(-0.1, 0.1, 0.001), dnorm(seq(-0.1, 0.1, 0.001), mean = mean(diff), sd = sd(diff)*0.73), col = 'orange')
lines(seq(-0.1, 0.1, 0.001), dcauchy(seq(-0.1, 0.1, 0.001), location = mean(diff), scale = 0.0077), col = 'blue')
- 赤線:変動率と同じ平均値、同じ標準偏差の正規分布
- 橙線:上記の正規分布で最頻値の高さを合わせるため標準偏差を0.73倍したもの
- 青線:コーシー分布
正規分布より株価の変動率の方が、平均値に近いところと平均値により離れたところで度数が多くなっています。また、平均値より離れたところを拡大してみると、
hist(diff, breaks = 100, freq = F, xlim = c(-0.1, -0.03), ylim = c(0, 4))
lines(seq(-0.1, 0.1, 0.001), dnorm(seq(-0.1, 0.1, 0.001), mean = mean(diff), sd = sd(diff)), col = 'red')
lines(seq(-0.1, 0.1, 0.001), dnorm(seq(-0.1, 0.1, 0.001), mean = mean(diff), sd = sd(diff)*0.73), col = 'orange')
lines(seq(-0.1, 0.1, 0.001), dcauchy(seq(-0.1, 0.1, 0.001), location = mean(diff), scale = 0.0077), col = 'blue')
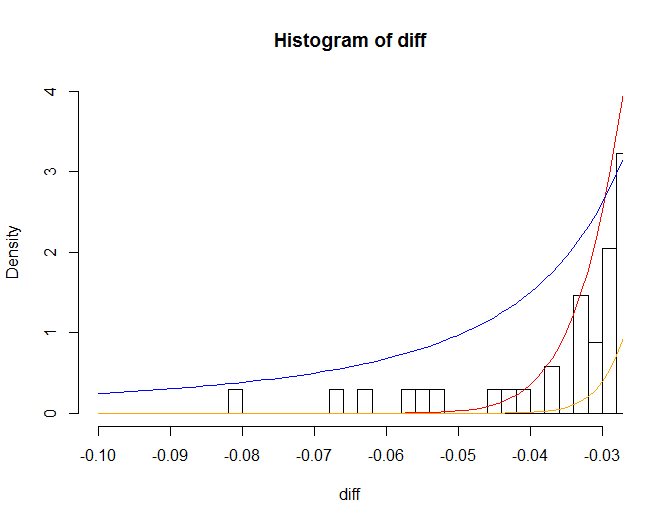
例えば、変動率が-0.08つまり、前日より終値で8%下落する度数が、正規分布ではほぼ0ですが実際の変動率ですと無視できない数存在します。標準偏差が0.013ですので-0.08は標準偏差の約6倍となり、正規分布では標準偏差の6倍の範囲に値が入る確率は99.999999%なので、それより外れる確率は、百万分の1となります。100万日に1回なのでおよそ2740年に1回のことが数年の株価の変動で発生してしまっています。正規分布では株価の変動を説明出来ないようですね。
念のためQQプロットは
# c.f. http://mizumot.com/handbook/?page_id=109
qqnorm(diff)
qqline(diff, col = 2)
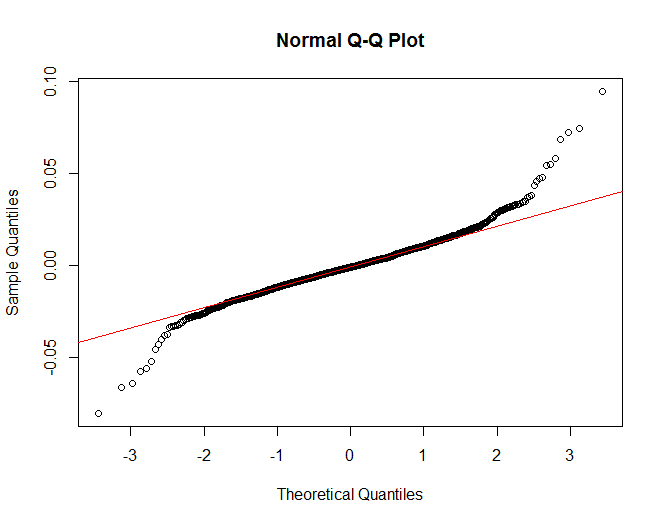
正規分布で想定される赤線より大きくずれています。
しつこく正規性の検定をしますと、
shapiro.test(diff)
Shapiro-Wilk normality test
data: diff
W = 0.951, p-value < 2.2e-16
ks.test(diff, "pnorm", mean=mean(diff), sd=sd(diff))
One-sample Kolmogorov-Smirnov test
data: diff
D = 0.053029, p-value = 0.0001361
alternative hypothesis: two-sided
p値が0.05を大きく下回り、データが正規分布に従っているという帰無仮説が棄却されます。
では、正規分布ではなくどういう分布かというと、べき分布の一種のコーシー分布に従うと言われているようです。コーシー分布は平均も分散も計算できない(最頻値はあり)という特異な分布です。平均も分散もないのでどう当てはめていいのか分かりませんが(今後の課題)仮にあてはめてみたのが上図の青線です。平均からはなれた位置でも比較的実際の度数に近い分布となっています。