『経済・ファイナンスデータの計量時系列分析』
の章末問題で「コンピュータを用いて」とあるものをRで解いています。
7.4
(1)
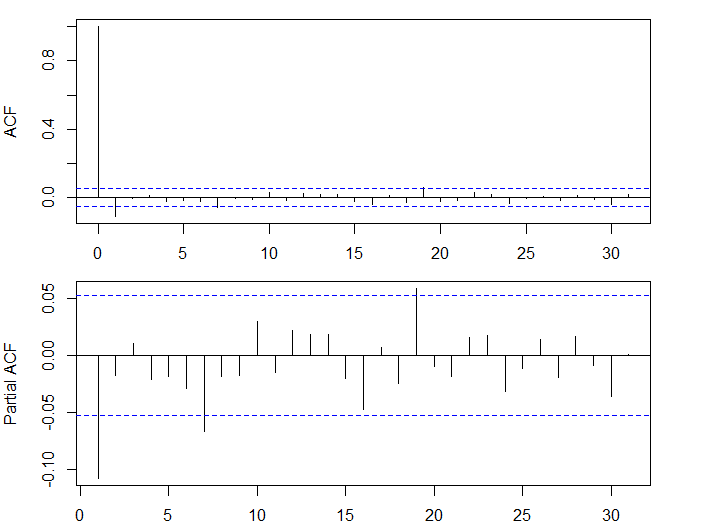
- 大きな自己相関はみられない
msci_day<-read.table("msci_day.txt",header=T)
par(mfrow=c(2,1))
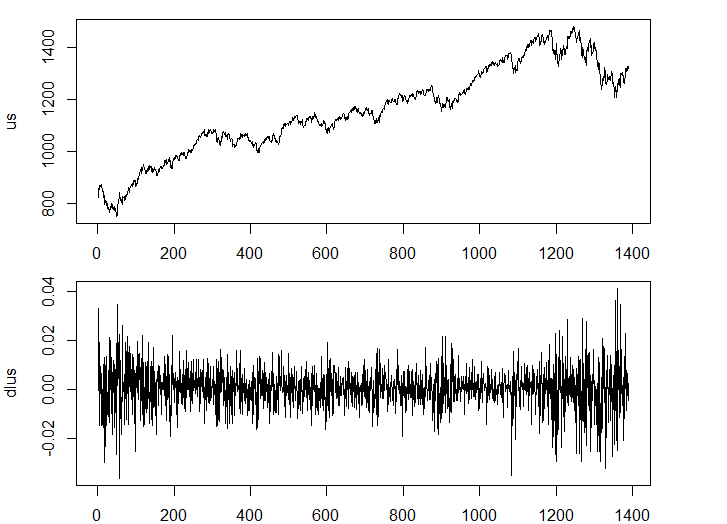
us<-msci_day$us
plot(us, type="l")
dlus<-diff(log(us))
plot(dlus, type="l")
acf(dlus)
pacf(dlus)
(2)
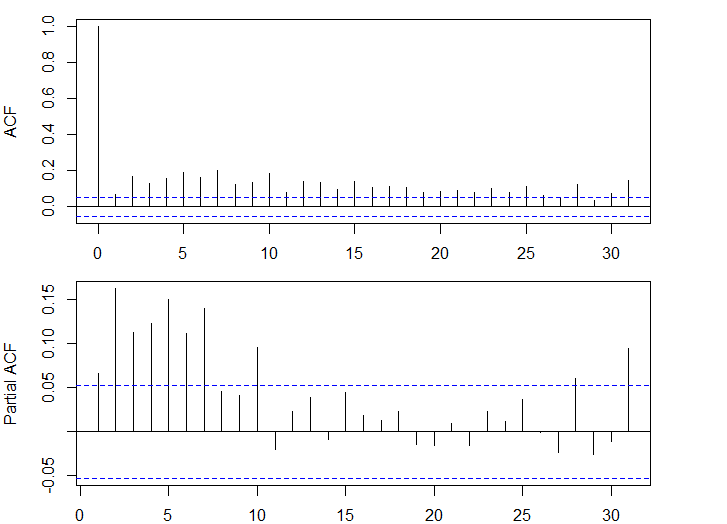
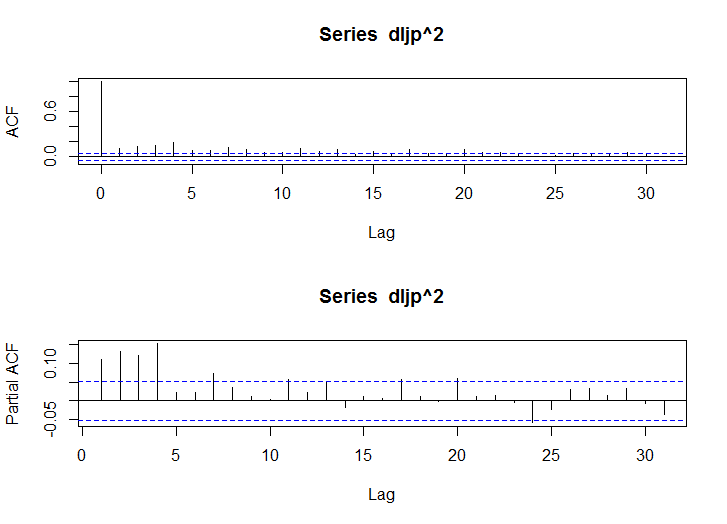
- 大きな自己相関がみられる
acf(dlus^2)
pacf(dlus^2)
(3)
# fGarch
library(fGarch)
dlus.garch<-garchFit(formula=~arma(1,0)+garch(1,1), data=dlus, trace=F)
summary(dlus.garch)
Title:
GARCH Modelling
Call:
garchFit(formula = ~arma(1, 0) + garch(1, 1), data = dlus, trace = F)
Mean and Variance Equation:
data ~ arma(1, 0) + garch(1, 1)
<environment: 0x0000000015605008>
[data = dlus]
Conditional Distribution:
norm
Coefficient(s):
mu ar1 omega alpha1
4.6782e-04 -7.8543e-02 1.0128e-06 5.0598e-02
beta1
9.3444e-01
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 4.678e-04 1.961e-04 2.386 0.01704 *
ar1 -7.854e-02 2.795e-02 -2.810 0.00495 **
omega 1.013e-06 3.489e-07 2.903 0.00370 **
alpha1 5.060e-02 9.937e-03 5.092 3.55e-07 ***
beta1 9.344e-01 1.314e-02 71.103 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Log Likelihood:
4756.516 normalized: 3.421954
Description:
Sun Jan 29 10:00:51 2017 by user: aoki
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 180.9516 0
Shapiro-Wilk Test R W 0.9840602 2.999756e-11
Ljung-Box Test R Q(10) 10.05805 0.4354152
Ljung-Box Test R Q(15) 14.6652 0.4757913
Ljung-Box Test R Q(20) 17.64631 0.6106947
Ljung-Box Test R^2 Q(10) 13.96237 0.174715
Ljung-Box Test R^2 Q(15) 16.33594 0.3600828
Ljung-Box Test R^2 Q(20) 17.08671 0.6473361
LM Arch Test R TR^2 15.48142 0.2161583
Information Criterion Statistics:
AIC BIC SIC HQIC
-6.836714 -6.817875 -6.836740 -6.829669
# rugarch
library(rugarch)
dlus.spec<-ugarchspec(variance.model=list(model="sGARCH", garchOrder=c(1,1)), mean.model=list(armaOrder=c(1,0), include.mean=T))
dlus.garch<-ugarchfit(data=dlus, spec=dlus.spec)
dlus.garch
> dlus.garch
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : sGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000441 0.000183 2.41849 0.015585
ar1 -0.079111 0.028059 -2.81940 0.004811
omega 0.000001 0.000002 0.59728 0.550317
alpha1 0.049525 0.020256 2.44490 0.014489
beta1 0.935539 0.023125 40.45591 0.000000
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000441 0.000355 1.243796 0.213575
ar1 -0.079111 0.027009 -2.929059 0.003400
omega 0.000001 0.000030 0.032807 0.973829
alpha1 0.049525 0.330906 0.149664 0.881029
beta1 0.935539 0.390027 2.398653 0.016455
LogLikelihood : 4751.628
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : sGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000441 0.000183 2.41849 0.015585
ar1 -0.079111 0.028059 -2.81940 0.004811
omega 0.000001 0.000002 0.59728 0.550317
alpha1 0.049525 0.020256 2.44490 0.014489
beta1 0.935539 0.023125 40.45591 0.000000
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000441 0.000355 1.243796 0.213575
ar1 -0.079111 0.027009 -2.929059 0.003400
omega 0.000001 0.000030 0.032807 0.973829
alpha1 0.049525 0.330906 0.149664 0.881029
beta1 0.935539 0.390027 2.398653 0.016455
LogLikelihood : 4751.628
Information Criteria
------------------------------------
Akaike -6.8297
Bayes -6.8108
Shibata -6.8297
Hannan-Quinn -6.8226
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.001242 0.9719
Lag[2*(p+q)+(p+q)-1][2] 0.385088 0.9856
Lag[4*(p+q)+(p+q)-1][5] 1.217200 0.9092
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 3.730 0.05345
Lag[2*(p+q)+(p+q)-1][5] 4.288 0.22027
Lag[4*(p+q)+(p+q)-1][9] 4.932 0.43945
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Information Criteria
------------------------------------
Akaike -6.8297
Bayes -6.8108
Shibata -6.8297
Hannan-Quinn -6.8226
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.001242 0.9719
Lag[2*(p+q)+(p+q)-1][2] 0.385088 0.9856
Lag[4*(p+q)+(p+q)-1][5] 1.217200 0.9092
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 3.730 0.05345
Lag[2*(p+q)+(p+q)-1][5] 4.288 0.22027
Lag[4*(p+q)+(p+q)-1][9] 4.932 0.43945
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.02518 0.500 2.000 0.8739
ARCH Lag[5] 1.14491 1.440 1.667 0.6905
ARCH Lag[7] 1.28023 2.315 1.543 0.8642
Statistic Shape Scale P-Value
ARCH Lag[3] 0.02518 0.500 2.000 0.8739
ARCH Lag[5] 1.14491 1.440 1.667 0.6905
ARCH Lag[7] 1.28023 2.315 1.543 0.8642
Nyblom stability test
------------------------------------
Joint Statistic: 162.9923
Individual Statistics:
mu 0.04725
ar1 0.15181
omega 16.76474
alpha1 0.32187
beta1 0.21276
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.28 1.47 1.88
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
Nyblom stability test
------------------------------------
Joint Statistic: 162.9923
Individual Statistics:
mu 0.04725
ar1 0.15181
omega 16.76474
alpha1 0.32187
beta1 0.21276
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.28 1.47 1.88
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 1.097 0.27267
Negative Sign Bias 1.033 0.30178
Positive Sign Bias 1.795 0.07293 *
Joint Effect 8.666 0.03408 **
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 88.73 5.556e-11
2 30 113.06 7.184e-12
3 40 110.26 1.005e-08
4 50 140.36 9.542e-11
Elapsed time : 1.15019
t-value prob sig
Sign Bias 1.097 0.27267
Negative Sign Bias 1.033 0.30178
Positive Sign Bias 1.795 0.07293 *
Joint Effect 8.666 0.03408 **
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 88.73 5.556e-11
2 30 113.06 7.184e-12
3 40 110.26 1.005e-08
4 50 140.36 9.542e-11
Elapsed time : 1.15019
-
fGarch
mu = 4.678e-04
ar1 =-7.854e-02
omega = 1.013e-06
alpha1= 5.060e-02
beta1 = 9.344e-01 -
rugarch
mu = 0.000441
ar1 =-0.079111
omega = 0.000001
alpha1= 0.049525
beta1 = 0.935539
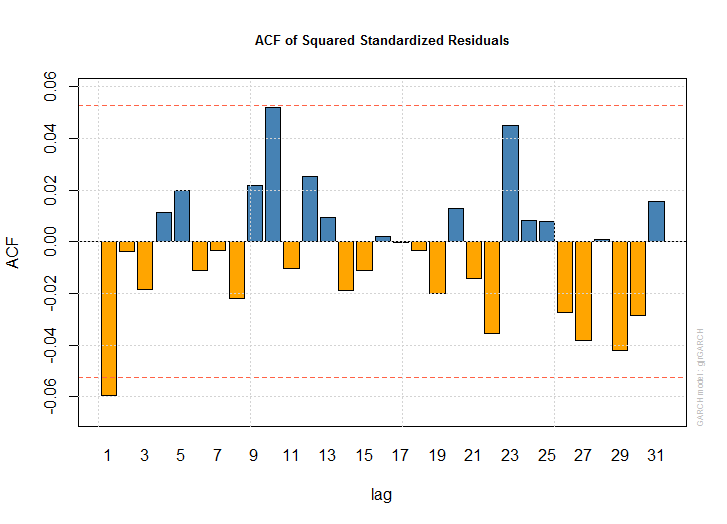
(4)
dlus.spec<-ugarchspec(variance.model=list(model="gjrGARCH", garchOrder=c(1,1)), mean.model=list(armaOrder=c(1,0), include.mean=T))
dlus.gjr<-ugarchfit(data=dlus, spec=dlus.spec)
dlus.gjr
> dlus.gjr<-ugarchfit(data=dlus, spec=dlus.spec)
> dlus.gjr
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : gjrGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000245 0.000183 1.340180 0.180187
ar1 -0.074942 0.027716 -2.703945 0.006852
omega 0.000001 0.000001 0.879222 0.379281
alpha1 0.000000 0.009631 0.000018 0.999986
beta1 0.943001 0.013853 68.069707 0.000000
gamma1 0.082897 0.019106 4.338717 0.000014
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000245 0.000157 1.559756 0.118818
ar1 -0.074942 0.023622 -3.172597 0.001511
omega 0.000001 0.000015 0.063334 0.949501
alpha1 0.000000 0.048887 0.000004 0.999997
beta1 0.943001 0.155045 6.082123 0.000000
gamma1 0.082897 0.149275 0.555334 0.578666
LogLikelihood : 4768.721
Information Criteria
------------------------------------
Akaike -6.8528
Bayes -6.8302
Shibata -6.8529
Hannan-Quinn -6.8444
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
> dlus.gjr
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : gjrGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000245 0.000183 1.340180 0.180187
ar1 -0.074942 0.027716 -2.703945 0.006852
omega 0.000001 0.000001 0.879222 0.379281
alpha1 0.000000 0.009631 0.000018 0.999986
beta1 0.943001 0.013853 68.069707 0.000000
gamma1 0.082897 0.019106 4.338717 0.000014
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000245 0.000157 1.559756 0.118818
ar1 -0.074942 0.023622 -3.172597 0.001511
omega 0.000001 0.000015 0.063334 0.949501
alpha1 0.000000 0.048887 0.000004 0.999997
beta1 0.943001 0.155045 6.082123 0.000000
gamma1 0.082897 0.149275 0.555334 0.578666
LogLikelihood : 4768.721
Information Criteria
------------------------------------
Akaike -6.8528
Bayes -6.8302
Shibata -6.8529
Hannan-Quinn -6.8444
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.003938 0.9500
Lag[2*(p+q)+(p+q)-1][2] 0.453423 0.9744
Lag[4*(p+q)+(p+q)-1][5] 1.435205 0.8622
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 4.918 0.02658
Lag[2*(p+q)+(p+q)-1][5] 5.404 0.12381
Lag[4*(p+q)+(p+q)-1][9] 6.045 0.29308
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
statistic p-value
Lag[1] 0.003938 0.9500
Lag[2*(p+q)+(p+q)-1][2] 0.453423 0.9744
Lag[4*(p+q)+(p+q)-1][5] 1.435205 0.8622
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 4.918 0.02658
Lag[2*(p+q)+(p+q)-1][5] 5.404 0.12381
Lag[4*(p+q)+(p+q)-1][9] 6.045 0.29308
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.4768 0.500 2.000 0.4899
ARCH Lag[5] 0.9559 1.440 1.667 0.7461
ARCH Lag[7] 1.1364 2.315 1.543 0.8904
Nyblom stability test
------------------------------------
Joint Statistic: 122.7693
Individual Statistics:
mu 0.1306
ar1 0.1738
omega 12.7333
alpha1 0.3491
beta1 0.1656
gamma1 0.2125
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.49 1.68 2.12
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.4768 0.500 2.000 0.4899
ARCH Lag[5] 0.9559 1.440 1.667 0.7461
ARCH Lag[7] 1.1364 2.315 1.543 0.8904
Nyblom stability test
------------------------------------
Joint Statistic: 122.7693
Individual Statistics:
mu 0.1306
ar1 0.1738
omega 12.7333
alpha1 0.3491
beta1 0.1656
gamma1 0.2125
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.49 1.68 2.12
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 1.559 0.11925
Negative Sign Bias 1.936 0.05303 *
Positive Sign Bias 1.467 0.14253
Joint Effect 9.124 0.02769 **
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 77.88 4.293e-09
2 30 86.60 1.202e-07
3 40 100.36 2.610e-07
4 50 103.09 1.006e-05
Elapsed time : 1.177835
t-value prob sig
Sign Bias 1.559 0.11925
Negative Sign Bias 1.936 0.05303 *
Positive Sign Bias 1.467 0.14253
Joint Effect 9.124 0.02769 **
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 77.88 4.293e-09
2 30 86.60 1.202e-07
3 40 100.36 2.610e-07
4 50 103.09 1.006e-05
Elapsed time : 1.177835
out<-data.frame()
omega<-1e-6
alpha<-1e-6
beta<-0.943001
gamma<-0.082897
ht<-seq(1,3)
for (ht1 in c(0.5,1,2)) {
i<-1
for (ut1 in -2:2) {
ht[i]<-omega+beta*ht1+alpha*ut1^2+gamma*ut1^2*sign(ut1<0)
i<-i+1
}
out<-rbind(out, ht)
}
names(out)<-c(-2, -1, 0, 1, 2)
row.names(out)<-c(0.5, 1, 2)
out
-2 -1 0 1 2
0.5 0.8030935 0.5543995 0.4715015 0.4715025 0.4715055
1 1.2745940 1.0259000 0.9430020 0.9430030 0.9430060
2 2.2175950 1.9689010 1.8860030 1.8860040 1.8860070
レバレッジ効果がある
(5)
- 11を選択
plot(dlus.garch)
plot(dlus.gjr)
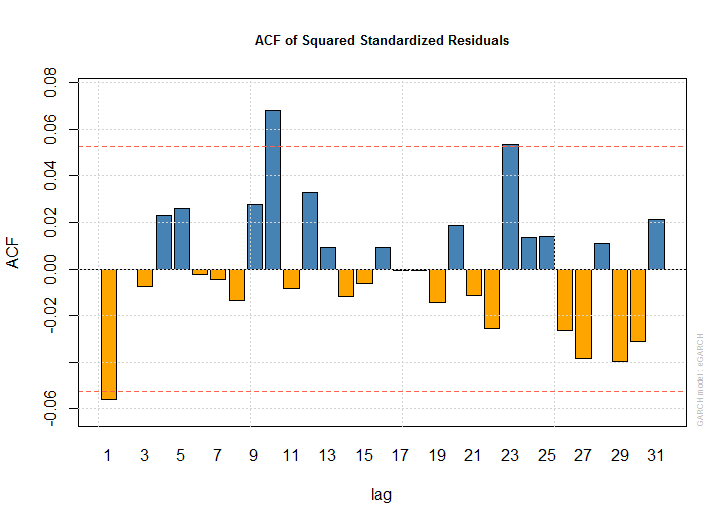
(6)
dlus.spec<-ugarchspec(variance.model=list(model="eGARCH", garchOrder=c(1,1)), mean.model=list(armaOrder=c(1,0), include.mean=T))
dlus.egarch<-ugarchfit(data=dlus, spec=dlus.spec)
dlus.egarch
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : eGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000277 0.000195 1.4201 0.155567
ar1 -0.081870 0.032705 -2.5033 0.012304
omega -0.166643 0.002957 -56.3473 0.000000
alpha1 -0.087830 0.012714 -6.9080 0.000000
beta1 0.982551 0.000020 48090.9514 0.000000
gamma1 0.078968 0.000391 202.0952 0.000000
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000277 0.000214 1.2924 0.196233
ar1 -0.081870 0.034178 -2.3954 0.016601
omega -0.166643 0.003663 -45.4988 0.000000
alpha1 -0.087830 0.012832 -6.8448 0.000000
beta1 0.982551 0.000024 40637.8939 0.000000
gamma1 0.078968 0.000521 151.5471 0.000000
LogLikelihood : 4767.201
Information Criteria
------------------------------------
Akaike -6.8506
Bayes -6.8280
Shibata -6.8507
Hannan-Quinn -6.8422
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.005655 0.9401
Lag[2*(p+q)+(p+q)-1][2] 0.504447 0.9632
Lag[4*(p+q)+(p+q)-1][5] 1.590462 0.8240
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 4.386 0.03624
Lag[2*(p+q)+(p+q)-1][5] 4.918 0.15978
Lag[4*(p+q)+(p+q)-1][9] 5.652 0.34020
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
-----------------------------------
GARCH Model : eGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000277 0.000195 1.4201 0.155567
ar1 -0.081870 0.032705 -2.5033 0.012304
omega -0.166643 0.002957 -56.3473 0.000000
alpha1 -0.087830 0.012714 -6.9080 0.000000
beta1 0.982551 0.000020 48090.9514 0.000000
gamma1 0.078968 0.000391 202.0952 0.000000
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000277 0.000214 1.2924 0.196233
ar1 -0.081870 0.034178 -2.3954 0.016601
omega -0.166643 0.003663 -45.4988 0.000000
alpha1 -0.087830 0.012832 -6.8448 0.000000
beta1 0.982551 0.000024 40637.8939 0.000000
gamma1 0.078968 0.000521 151.5471 0.000000
LogLikelihood : 4767.201
Information Criteria
------------------------------------
Akaike -6.8506
Bayes -6.8280
Shibata -6.8507
Hannan-Quinn -6.8422
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.005655 0.9401
Lag[2*(p+q)+(p+q)-1][2] 0.504447 0.9632
Lag[4*(p+q)+(p+q)-1][5] 1.590462 0.8240
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 4.386 0.03624
Lag[2*(p+q)+(p+q)-1][5] 4.918 0.15978
Lag[4*(p+q)+(p+q)-1][9] 5.652 0.34020
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.07761 0.500 2.000 0.7806
ARCH Lag[5] 1.23064 1.440 1.667 0.6659
ARCH Lag[7] 1.39694 2.315 1.543 0.8418
Nyblom stability test
------------------------------------
Joint Statistic: 2.5097
Individual Statistics:
mu 0.2007
ar1 0.1198
omega 0.2873
alpha1 1.2433
beta1 0.2688
gamma1 0.2354
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.49 1.68 2.12
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 1.441 0.14975
Negative Sign Bias 1.967 0.04941 **
Positive Sign Bias 1.387 0.16578
Joint Effect 8.142 0.04317 **
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 74.78 1.452e-08
2 30 83.45 3.577e-07
3 40 87.99 1.202e-05
4 50 119.64 7.685e-08
Elapsed time : 0.8469431
Statistic Shape Scale P-Value
ARCH Lag[3] 0.07761 0.500 2.000 0.7806
ARCH Lag[5] 1.23064 1.440 1.667 0.6659
ARCH Lag[7] 1.39694 2.315 1.543 0.8418
Nyblom stability test
------------------------------------
Joint Statistic: 2.5097
Individual Statistics:
mu 0.2007
ar1 0.1198
omega 0.2873
alpha1 1.2433
beta1 0.2688
gamma1 0.2354
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.49 1.68 2.12
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 1.441 0.14975
Negative Sign Bias 1.967 0.04941 **
Positive Sign Bias 1.387 0.16578
Joint Effect 8.142 0.04317 **
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 74.78 1.452e-08
2 30 83.45 3.577e-07
3 40 87.99 1.202e-05
4 50 119.64 7.685e-08
Elapsed time : 0.8469431
out<-data.frame()
omega<--0.166646
alpha<--0.087830
beta<-0.982551
gamma<-0.078968
ht<-seq(1,3)
for (ht1 in c(0.5,1,2)) {
i<-1
for (ut1 in -2:2) {
ht[i]<-omega+beta*ht1+alpha*ut1^2+gamma*ut1^2*sign(ut1<0)
i<-i+1
}
out<-rbind(out, ht)
}
names(out)<-c(-2, -1, 0, 1, 2)
row.names(out)<-c(0.5, 1, 2)
out
-2 -1 0 1 2
0.5 0.2891845 0.3157705 0.3246325 0.2368025 -0.0266875
1 0.7804600 0.8070460 0.8159080 0.7280780 0.4645880
2 1.7630110 1.7895970 1.7984590 1.7106290 1.4471390
-2 -1 0 1 2
0.5 0.2891845 0.3157705 0.3246325 0.2368025 -0.0266875
1 0.7804600 0.8070460 0.8159080 0.7280780 0.4645880
2 1.7630110 1.7895970 1.7984590 1.7106290 1.4471390
レバレッジ効果がある
(7)
- 11を選択
plot(dlus.egarch)
(8)
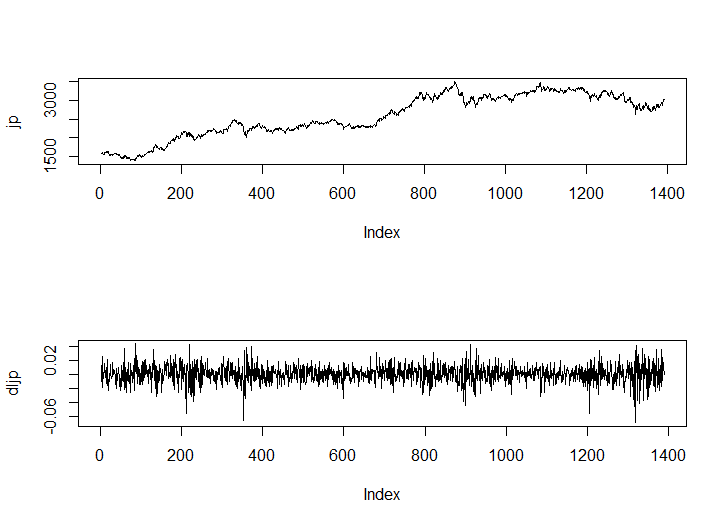
par(mfrow=c(2,1))
jp<-msci_day$jp
plot(jp, type="l")
dljp<-diff(log(jp))
plot(dljp, type="l")
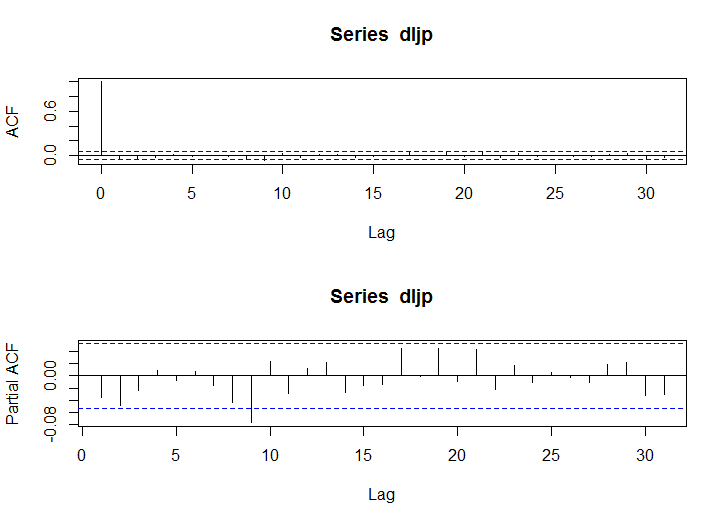
acf(dljp)
pacf(dljp)
acf(dljp^2)
pacf(dljp^2)
# GARCH
dljp.spec<-ugarchspec(variance.model=list(model="sGARCH", garchOrder=c(1,1)), mean.model=list(armaOrder=c(1,0), include.mean=T))
dljp.garch<-ugarchfit(data=dljp, spec=dljp.spec)
dljp.garch
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : sGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000566 0.000298 1.90212 0.057156
ar1 -0.010948 0.028309 -0.38675 0.698944
omega 0.000005 0.000003 1.39533 0.162918
alpha1 0.083277 0.003737 22.28493 0.000000
beta1 0.889458 0.011228 79.22073 0.000000
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000566 0.000282 2.00790 0.044653
ar1 -0.010948 0.025292 -0.43289 0.665098
omega 0.000005 0.000011 0.43276 0.665188
alpha1 0.083277 0.040851 2.03853 0.041497
beta1 0.889458 0.027516 32.32567 0.000000
LogLikelihood : 4150.981
Information Criteria
------------------------------------
Akaike -5.9654
Bayes -5.9466
Shibata -5.9655
Hannan-Quinn -5.9584
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.02266 0.8803
Lag[2*(p+q)+(p+q)-1][2] 1.08159 0.6901
Lag[4*(p+q)+(p+q)-1][5] 1.86771 0.7491
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.1186 0.7306
Lag[2*(p+q)+(p+q)-1][5] 1.1543 0.8239
Lag[4*(p+q)+(p+q)-1][9] 2.5367 0.8323
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.002486 0.500 2.000 0.9602
ARCH Lag[5] 2.041177 1.440 1.667 0.4622
ARCH Lag[7] 2.500743 2.315 1.543 0.6123
Nyblom stability test
------------------------------------
Joint Statistic: 1.3237
Individual Statistics:
mu 0.12216
ar1 0.63447
omega 0.07506
alpha1 0.10576
beta1 0.12412
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.28 1.47 1.88
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
statistic p-value
Lag[1] 0.02266 0.8803
Lag[2*(p+q)+(p+q)-1][2] 1.08159 0.6901
Lag[4*(p+q)+(p+q)-1][5] 1.86771 0.7491
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.1186 0.7306
Lag[2*(p+q)+(p+q)-1][5] 1.1543 0.8239
Lag[4*(p+q)+(p+q)-1][9] 2.5367 0.8323
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.002486 0.500 2.000 0.9602
ARCH Lag[5] 2.041177 1.440 1.667 0.4622
ARCH Lag[7] 2.500743 2.315 1.543 0.6123
Nyblom stability test
------------------------------------
Joint Statistic: 1.3237
Individual Statistics:
mu 0.12216
ar1 0.63447
omega 0.07506
alpha1 0.10576
beta1 0.12412
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.28 1.47 1.88
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 0.3668 0.71379
Negative Sign Bias 0.8259 0.40900
Positive Sign Bias 1.8655 0.06233 *
Joint Effect 6.9489 0.07354 *
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 26.43 0.11860
2 30 41.88 0.05751
3 40 46.26 0.19758
4 50 51.80 0.36520
Elapsed time : 1.276816
t-value prob sig
Sign Bias 0.3668 0.71379
Negative Sign Bias 0.8259 0.40900
Positive Sign Bias 1.8655 0.06233 *
Joint Effect 6.9489 0.07354 *
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 26.43 0.11860
2 30 41.88 0.05751
3 40 46.26 0.19758
4 50 51.80 0.36520
Elapsed time : 1.276816
# GJR
dljp.spec<-ugarchspec(variance.model=list(model="gjrGARCH", garchOrder=c(1,1)), mean.model=list(armaOrder=c(1,0), include.mean=T))
dljp.gjr<-ugarchfit(data=dljp, spec=dljp.spec)
dljp.gjr
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : gjrGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000304 0.000304 0.999384 0.317609
ar1 -0.001567 0.028243 -0.055491 0.955747
omega 0.000007 0.000000 20.873872 0.000000
alpha1 0.017432 0.006800 2.563331 0.010367
beta1 0.877409 0.010546 83.198403 0.000000
gamma1 0.123741 0.025443 4.863400 0.000001
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000304 0.000282 1.07554 0.282131
ar1 -0.001567 0.026541 -0.05905 0.952912
omega 0.000007 0.000000 24.15722 0.000000
alpha1 0.017432 0.007349 2.37207 0.017689
beta1 0.877409 0.008430 104.07677 0.000000
gamma1 0.123741 0.031752 3.89708 0.000097
LogLikelihood : 4162.846
Information Criteria
------------------------------------
Akaike -5.9811
Bayes -5.9585
Shibata -5.9811
Hannan-Quinn -5.9726
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : gjrGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000304 0.000304 0.999384 0.317609
ar1 -0.001567 0.028243 -0.055491 0.955747
omega 0.000007 0.000000 20.873872 0.000000
alpha1 0.017432 0.006800 2.563331 0.010367
beta1 0.877409 0.010546 83.198403 0.000000
gamma1 0.123741 0.025443 4.863400 0.000001
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000304 0.000282 1.07554 0.282131
ar1 -0.001567 0.026541 -0.05905 0.952912
omega 0.000007 0.000000 24.15722 0.000000
alpha1 0.017432 0.007349 2.37207 0.017689
beta1 0.877409 0.008430 104.07677 0.000000
gamma1 0.123741 0.031752 3.89708 0.000097
LogLikelihood : 4162.846
Information Criteria
------------------------------------
Akaike -5.9811
Bayes -5.9585
Shibata -5.9811
Hannan-Quinn -5.9726
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.07495 0.7843
Lag[2*(p+q)+(p+q)-1][2] 0.99937 0.7403
Lag[4*(p+q)+(p+q)-1][5] 1.76512 0.7776
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.6437 0.4224
Lag[2*(p+q)+(p+q)-1][5] 2.0086 0.6164
Lag[4*(p+q)+(p+q)-1][9] 3.0480 0.7510
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.3121 0.500 2.000 0.5764
ARCH Lag[5] 1.5248 1.440 1.667 0.5858
ARCH Lag[7] 1.6458 2.315 1.543 0.7917
Nyblom stability test
------------------------------------
Joint Statistic: 21.5161
Individual Statistics:
mu 0.2835
ar1 0.8198
omega 4.1418
alpha1 0.2854
beta1 0.2736
gamma1 0.1365
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.49 1.68 2.12
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
statistic p-value
Lag[1] 0.07495 0.7843
Lag[2*(p+q)+(p+q)-1][2] 0.99937 0.7403
Lag[4*(p+q)+(p+q)-1][5] 1.76512 0.7776
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.6437 0.4224
Lag[2*(p+q)+(p+q)-1][5] 2.0086 0.6164
Lag[4*(p+q)+(p+q)-1][9] 3.0480 0.7510
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.3121 0.500 2.000 0.5764
ARCH Lag[5] 1.5248 1.440 1.667 0.5858
ARCH Lag[7] 1.6458 2.315 1.543 0.7917
Nyblom stability test
------------------------------------
Joint Statistic: 21.5161
Individual Statistics:
mu 0.2835
ar1 0.8198
omega 4.1418
alpha1 0.2854
beta1 0.2736
gamma1 0.1365
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.49 1.68 2.12
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 0.4724 0.6367
Negative Sign Bias 0.4875 0.6260
Positive Sign Bias 0.8604 0.3897
Joint Effect 2.1598 0.5399
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 25.08 0.1580
2 30 35.54 0.1874
3 40 36.42 0.5883
4 50 51.44 0.3785
Elapsed time : 0.350035
out<-data.frame()
omega<--0.361037
alpha<-0.017432
beta<-0.877409
gamma<-0.123741
ht<-seq(1,3)
for (ht1 in c(0.5,1,2)) {
i<-1
for (ut1 in -2:2) {
ht[i]<-omega+beta*ht1+alpha*ut1^2+gamma*ut1^2*sign(ut1<0)
i<-i+1
}
out<-rbind(out, ht)
}
names(out)<-c(-2, -1, 0, 1, 2)
row.names(out)<-c(0.5, 1, 2)
out
-2 -1 0 1 2
0.5 1.003403 0.5798845 0.4387115 0.4561435 0.5084395
1 1.442108 1.0185890 0.8774160 0.8948480 0.9471440
2 2.319517 1.8959980 1.7548250 1.7722570 1.8245530
-2 -1 0 1 2
0.5 1.003403 0.5798845 0.4387115 0.4561435 0.5084395
1 1.442108 1.0185890 0.8774160 0.8948480 0.9471440
2 2.319517 1.8959980 1.7548250 1.7722570 1.8245530
# EGARCH
dljp.spec<-ugarchspec(variance.model=list(model="eGARCH", garchOrder=c(1,1)), mean.model=list(armaOrder=c(1,0), include.mean=T))
dljp.egarch<-ugarchfit(data=dljp, spec=dljp.spec)
dljp.egarch
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : eGARCH(1,1)
Mean Model : ARFIMA(1,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.000191 0.000377 0.50733 0.611924
ar1 -0.003791 0.029245 -0.12961 0.896873
omega -0.361037 0.232596 -1.55220 0.120614
alpha1 -0.088885 0.037871 -2.34705 0.018923
beta1 0.958573 0.026242 36.52825 0.000000
gamma1 0.168848 0.079853 2.11450 0.034473
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.000191 0.000874 0.218611 0.82695
ar1 -0.003791 0.039681 -0.095524 0.92390
omega -0.361037 0.898477 -0.401832 0.68781
alpha1 -0.088885 0.134327 -0.661703 0.50816
beta1 0.958573 0.101299 9.462813 0.00000
gamma1 0.168848 0.309855 0.544926 0.58581
LogLikelihood : 4162.689
Information Criteria
------------------------------------
Akaike -5.9808
Bayes -5.9582
Shibata -5.9809
Hannan-Quinn -5.9724
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.1264 0.7222
Lag[2*(p+q)+(p+q)-1][2] 1.2006 0.6159
Lag[4*(p+q)+(p+q)-1][5] 2.0282 0.7032
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.6199 0.4311
Lag[2*(p+q)+(p+q)-1][5] 1.9735 0.6247
Lag[4*(p+q)+(p+q)-1][9] 3.1966 0.7261
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
statistic p-value
Lag[1] 0.1264 0.7222
Lag[2*(p+q)+(p+q)-1][2] 1.2006 0.6159
Lag[4*(p+q)+(p+q)-1][5] 2.0282 0.7032
d.o.f=1
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.6199 0.4311
Lag[2*(p+q)+(p+q)-1][5] 1.9735 0.6247
Lag[4*(p+q)+(p+q)-1][9] 3.1966 0.7261
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.04281 0.500 2.000 0.8361
ARCH Lag[5] 1.73869 1.440 1.667 0.5319
ARCH Lag[7] 1.91168 2.315 1.543 0.7360
Nyblom stability test
------------------------------------
Joint Statistic: 1.6343
Individual Statistics:
mu 0.32484
ar1 0.81875
omega 0.26270
alpha1 0.19614
beta1 0.26888
gamma1 0.02107
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.49 1.68 2.12
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 0.1859 0.8525
Negative Sign Bias 0.4346 0.6640
Positive Sign Bias 1.0319 0.3023
Joint Effect 1.9371 0.5856
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 33.02 0.0239
2 30 32.99 0.2780
3 40 41.02 0.3820
4 50 49.14 0.4676
Elapsed time : 0.663059
Statistic Shape Scale P-Value
ARCH Lag[3] 0.04281 0.500 2.000 0.8361
ARCH Lag[5] 1.73869 1.440 1.667 0.5319
ARCH Lag[7] 1.91168 2.315 1.543 0.7360
Nyblom stability test
------------------------------------
Joint Statistic: 1.6343
Individual Statistics:
mu 0.32484
ar1 0.81875
omega 0.26270
alpha1 0.19614
beta1 0.26888
gamma1 0.02107
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.49 1.68 2.12
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 0.1859 0.8525
Negative Sign Bias 0.4346 0.6640
Positive Sign Bias 1.0319 0.3023
Joint Effect 1.9371 0.5856
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 33.02 0.0239
2 30 32.99 0.2780
3 40 41.02 0.3820
4 50 49.14 0.4676
Elapsed time : 0.663059
out<-data.frame()
omega<-0.000191
alpha<--0.088884
beta<-0.958573
gamma<-0.168848
ht<-seq(1,3)
for (ht1 in c(0.5,1,2)) {
i<-1
for (ut1 in -2:2) {
ht[i]<-omega+beta*ht1+alpha*ut1^2+gamma*ut1^2*sign(ut1<0)
i<-i+1
}
out<-rbind(out, ht)
}
names(out)<-c(-2, -1, 0, 1, 2)
row.names(out)<-c(0.5, 1, 2)
out
-2 -1 0 1 2
0.5 0.4381015 0.1982125 0.1182495 0.0293645 -0.2372905
1 0.9173880 0.6774990 0.5975360 0.5086510 0.2419960
2 1.8759610 1.6360720 1.5561090 1.4672240 1.2005690
-2 -1 0 1 2
0.5 0.4381015 0.1982125 0.1182495 0.0293645 -0.2372905
1 0.9173880 0.6774990 0.5975360 0.5086510 0.2419960
2 1.8759610 1.6360720 1.5561090 1.4672240 1.2005690
- 11を選択
plot(dljp.garch)
plot(dljp.gjr)
plot(dljp.egarch)
7.5
DVEC, BEKK, CCC
- 他のモデルの関数が分からずCCCモデルのみ
library(ccgarch)
msci_day<-read.table("msci_day.txt",header=T)
jp<-msci_day$jp
uk<-msci_day$uk
us<-msci_day$us
data<-as.matrix(msci_day[,6:8])
a<-c(0.003, 0.005, 0.001)
A<-diag(c(0.2, 0.3, 0.15))
B<-diag(c(0.79, 0.6, 0.8))
R<-matrix(c(cor(jp,jp), cor(jp,uk), cor(jp,us), cor(uk,jp), cor(uk,uk), cor(uk,us), cor(us,jp), cor(us,uk), cor(us,us)), 3, 3)
eccc.estimation(a, A, B, R, data, model="diagonal")
でよいと思うが、
Error in solve.default(H) :
system is computationally singular: reciprocal condition number = 1.26294e-21
Error in solve.default(H) :
system is computationally singular: reciprocal condition number = 1.26294e-21