More than 5 years have passed since last update.

Machine LearningAdvent Calendar 2016

@antimon2(Shunsuke GOTOH)in

有限会社来栖川電算

AdaBoost の弱学習器を色々試してみた

Posted at 2016-12-04

初めに

この記事は、Machine Learning Advent Calendar 2016 5日目の記事です。

複数の学習器（弱学習器、weak learner）を組み合わせてよりより性能の高い学習器（強学習器、strong learner）を作る、アンサンブル学習の手法の一つ、ブースティング。
その中でも代表的な、AdaBoost。

PRML本にも載っている（日本語版下巻p.374）しググれば実装例もいくらでも出てきますけれど、弱学習器として一番単純な決定株（decision stump）を用いた例ばかり。
それを他のものに変えたら、性能にどう影響するか。思いつきで実験してみました。¹

実験環境

Mac OSX 10.11.6
Core i7 3.1GHz / 16GB RAM
Julia v0.5.0
- IJulia（Julia の Jupyter カーネル）、Gadfly（Julia定番のプロットライブラリ）以外の特別な外部パッケージは不使用。

実験に使用した二値分類データ

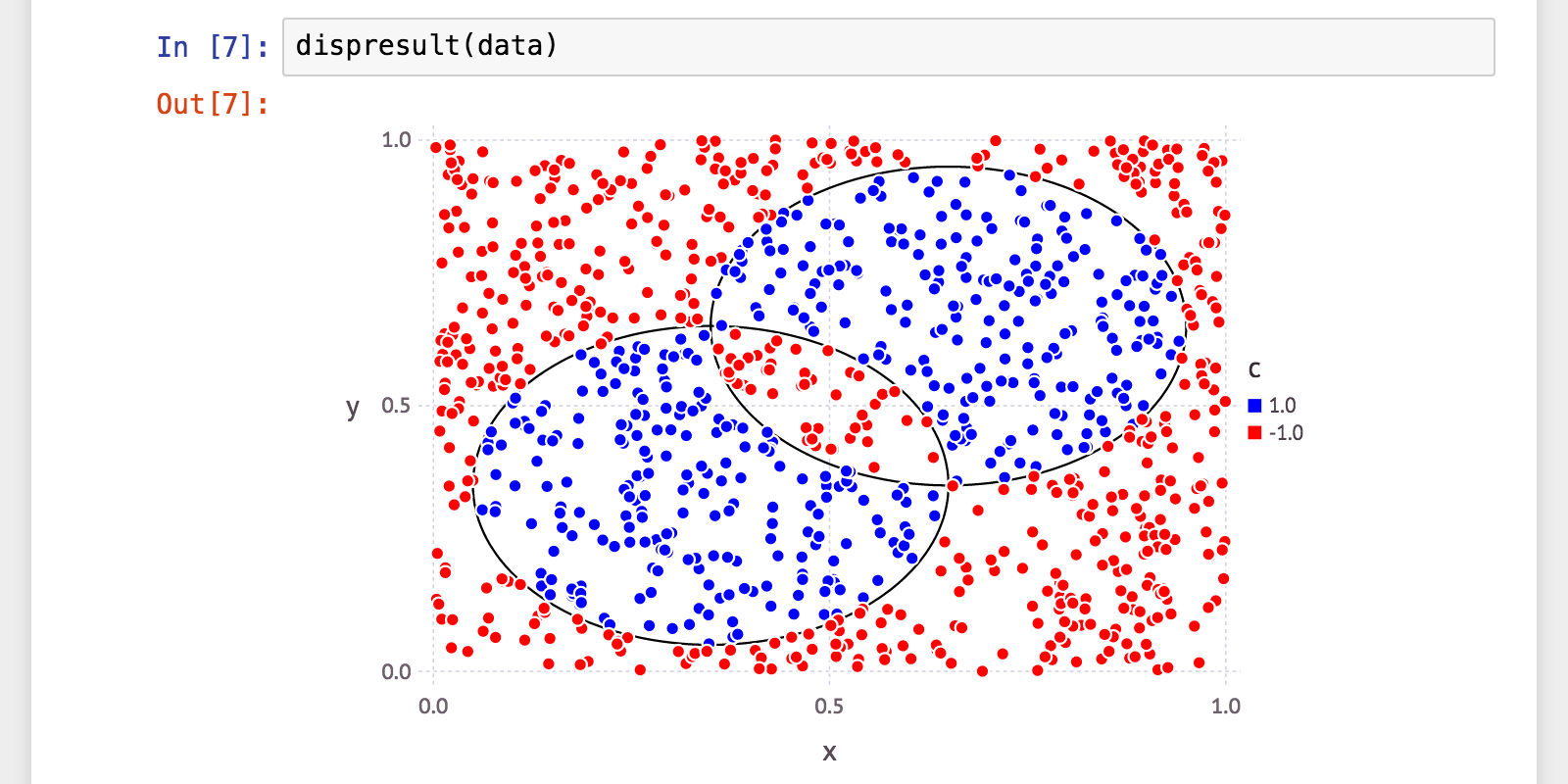
ほぼ個人的な興味で、以下のようなデータを二値分類してみたいと思いました。

一部が重なり合った二つの円があって、その「いずれか一方のみ」の内部の点と、それ以外。
これがキレイに分類できる分類器ができれば、気持ちよいですよね²。

なお、データは以下のような関数を作って実験（訓練、及びテスト）ごとにランダム生成しました。

# サンプルデータ（訓練データ）生成
function makelabels{T<:AbstractFloat}(data::AbstractMatrix{T})
    # 円1：中心 (0.35, 0.35), 半径 0.3 の円
    x1 = 0.35; y1 = 0.35; r1 = 0.3
    # 円2：中心 (0.65, 0.65), 半径 0.3 の円
    x2 = 0.65; y2 = 0.65; r2 = 0.3
    # 円1 と 円2 どちらかに（のみ）入っているならば 1、そうでなければ 0
    chk1 = mapslices(norm, data .- [x1 y1;], 2) .<= r1
    chk2 = mapslices(norm, data .- [x2 y2;], 2) .<= r2
    vec(collect(T, chk1 $ chk2)) .* 2 .- 1
end

# サンプルデータ（訓練データ）生成
function makedata(N::Int=1000)
    data = rand(N, 2)
    labels = makelabels(data)
    DataFrame(x=vec(data[:,1]), y=vec(data[:,2]), c=vec(labels))
end

AdaBoost 実装

実装はこんな感じ³⁴：

adaboost.jl

function _signplus{T<:AbstractFloat}(x::T)
    x == 0 ? one(T) : sign(x)
end

function _signplus{T<:AbstractFloat, N}(x::AbstractArray{T, N})
    broadcast(_signplus, x)
end

abstract WeakClassifier{T<:AbstractFloat}

include("decisionstumpweakclassifier.jl")

immutable AdaBoost{T<:AbstractFloat, W<:WeakClassifier}
    alpha::AbstractVector{T}
    hs::AbstractVector{W}
end

function adaboost{T<:AbstractFloat, WC<:WeakClassifier}(
        X::AbstractMatrix{T},
        Y::AbstractVector{T};
        wc::Type{WC}=DecisionStumpWeakClassifier,
        t=100,
        kwds...)
    M = length(Y)
    D = ones(T, M) ./ M
    hs = WC{T}[]
    alpha = T[]
    for _ = 1:t
        h = weaklearn(wc, X, Y, D; kwds...)
        diff = abs(h(X) - Y)
        e = dot(diff, D) / 2
        if e < 1e-10
            break
        end
        a = log((1 - e) / e) / 2
        D .*= exp(a .* (diff - 1))
        D ./= sum(D)
        push!(hs, h)
        push!(alpha, a)
    end
    AdaBoost(alpha, hs)
end

function (f::AdaBoost{T,W}){T<:AbstractFloat,W}(x::AbstractVector{T})
    _signplus(dot(f.alpha, [h(x) for h=f.hs]))
end

function (f::AdaBoost{T,W}){T<:AbstractFloat,W}(x::AbstractMatrix{T})
    mapslices(f, x, 2)
end

decisionstumpweakclassifier.jl

immutable DecisionStumpWeakClassifier{T<:AbstractFloat} <: WeakClassifier{T}
    axis::Int
    d::T
    b::T
end

function weaklearn{T<:AbstractFloat}(
        ::Type{DecisionStumpWeakClassifier},
        X::AbstractMatrix{T},
        Y::AbstractVector{T},
        D::AbstractVector{T})
    # @assert size(X)[1] == length(Y) == length(D)
    (N, M) = size(X)
    tgtidx = rand(1:M)
    xi = sortperm(X[:,tgtidx])
    WY = Y .* D
    el = cumsum(WY[xi])
    eu = cumsum(WY[reverse(xi)])
    es = eu[end-1:-1:1] .- el[1:end-1]
    idx = indmax(abs(es))
    d = sign(es[idx])
    b = (X[xi[idx],tgtidx] + X[xi[idx + 1],tgtidx]) / 2
    DecisionStumpWeakClassifier(tgtidx, d, b)
end
@inline weaklearn(::Type{DecisionStumpWeakClassifier}, X, Y, D; kwds...) = 
    weaklearn(DecisionStumpWeakClassifier, X, Y, D)

function (h::DecisionStumpWeakClassifier{T}){T}(x::AbstractMatrix{T})
    _signplus(h.d .* (x[:,h.axis] .- h.b))
end

function (h::DecisionStumpWeakClassifier{T}){T}(x::AbstractVector{T})
    _signplus(h.d * (x[h.axis] - h.b))
end

決定株（Decision Stump）の学習部分は、イラストで学ぶ機械学習に記載の MATLAB プログラム例を参考にしました。cumsum して差を取ることで簡単高速に「最適な境界」が求まります。目からウロコ。
あと、WeakClassifier を継承した型と、それを受け取る weaklearn() 関数を（多重）定義することによって、弱学習器（弱分類器）をプラグイン的に差し替えられるようにしておきました。オプション指定（キーワード引数）となっており、未指定時はデフォルトで決定株が利用されるようにしてあります。

決定株（Decision Stump）を弱学習器とした学習・分類

t=1000

さて早速学習・分類してみましょう。まずは、弱学習器（決定株）を最大 1000個で試してみます。

julia> X = convert(Array, data[:,1:2]); Y = collect(data[:, 3]);

julia> include("adaboost.jl")

julia> H = adaboost(X, Y; t=1000)
AdaBoost{Float64,DecisionStumpWeakClassifier{Float64}}([…《略》

julia> length(H.alpha)
1000

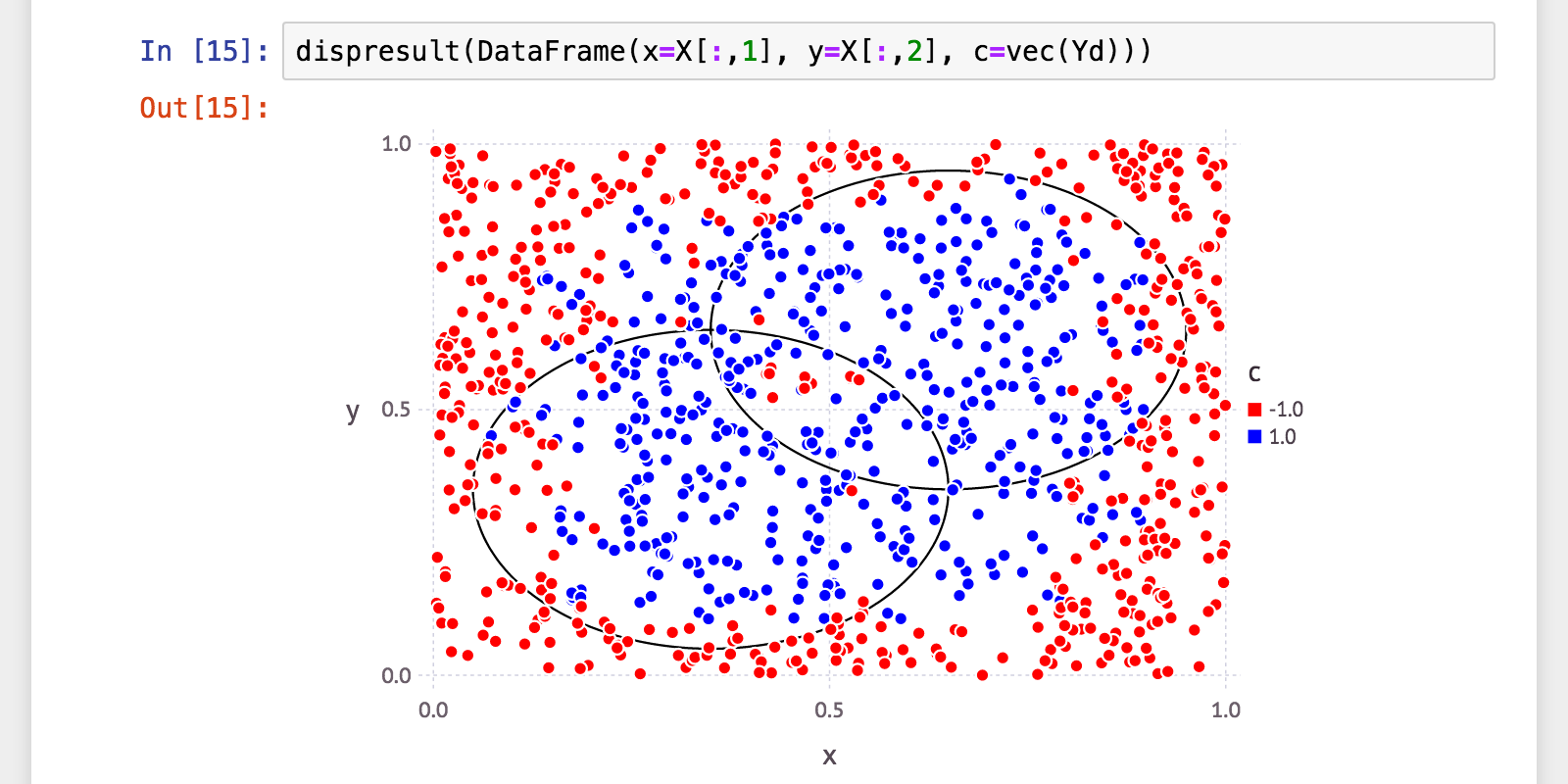
julia> Yd = H(X);

うーん…今ひとつきちんと分類できてないですね…。

性能評価

正答率・適合率・再現率・F-値（F1-measure）を算出してみます。

function calc_confusionmatrix(Y, Yd)
    tp = sum(1+Y[Yd.==1])/2
    fp = sum(1-Y[Yd.==1])/2
    tn = sum(1-Y[Yd.==-1])/2
    fn = sum(1+Y[Yd.==-1])/2
    [tp fp; fn tn]
end

function calc_mlmetrics(Y, Yd)
    cm = calc_confusionmatrix(Y, Yd)
    (tp, fn, fp, tn) = vec(cm)
    accuracy = (tp + tn) / (tp + fp + fn + tn)
    precision_score = tp / (tp + fp)
    recall_score = tp / (tp + fn)
    f_measure = 2 * precision_score * recall_score / (precision_score + recall_score)
    (accuracy, precision_score, recall_score, f_measure)
end

julia> (a, p, r, f) = calc_mlmetrics(Y, Yd);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.817000

julia> @printf("precision: %.06f\n", p)
precision: 0.774194

julia> @printf("recall: %.06f\n", r)
recall: 0.821918

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.797342

やっぱり今ひとつ。

汎化性能

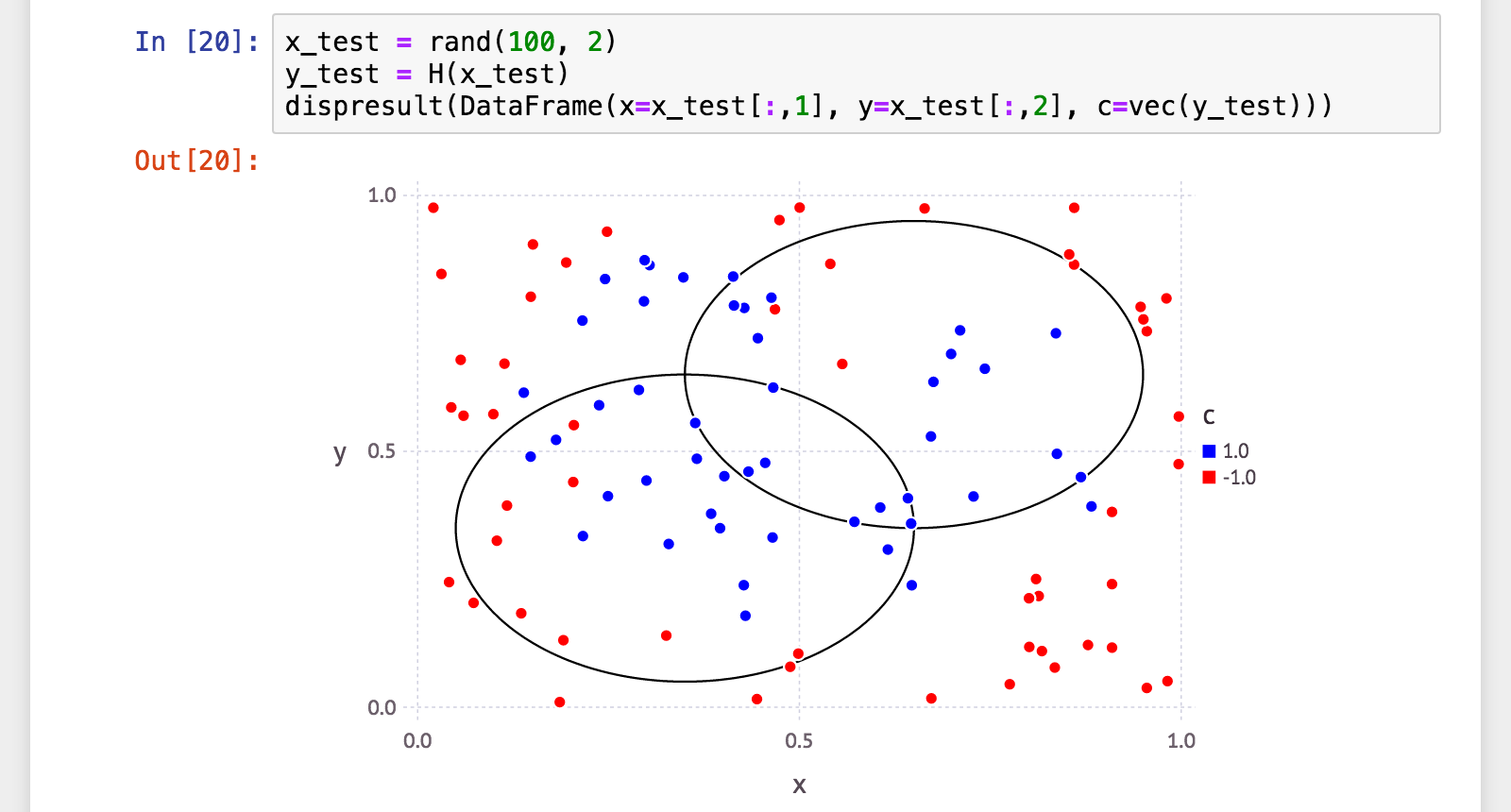
テストデータでも確認。

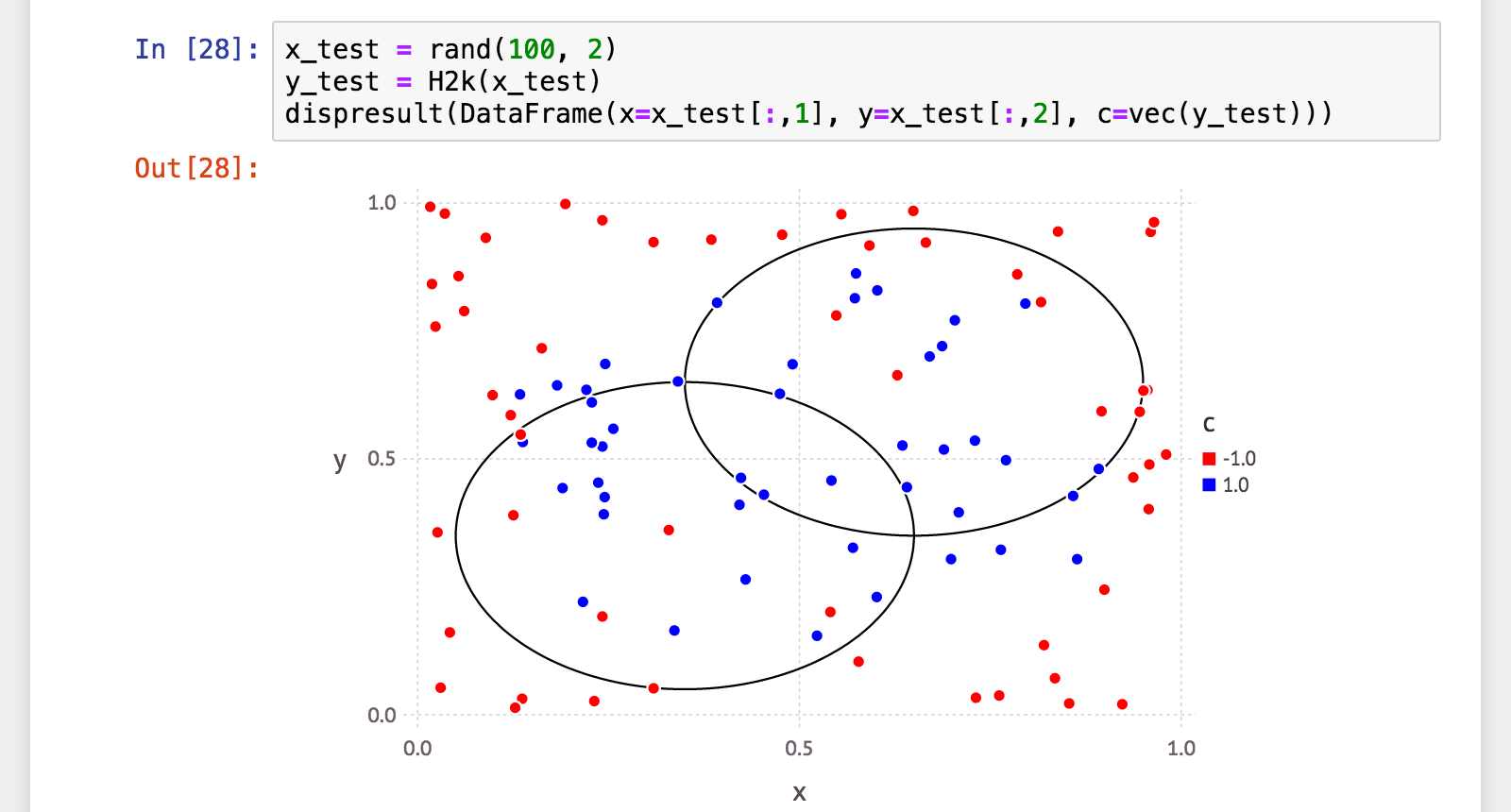
julia> x_test = rand(100, 2);

julia> y_test = H(x_test);

julia> (a, p, r, f) = calc_mlmetrics(makelabels(x_test), y_test);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.720000

julia> @printf("precision: %.06f\n", p)
precision: 0.638298

julia> @printf("recall: %.06f\n", r)
recall: 0.731707

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.681818

よろしくないですね＞＜

t=2000

弱学習器（弱分類器）を 1000個から 2000個に増やしてみました。

julia> H2k = adaboost(X, Y; t=2000)
AdaBoost{Float64,DecisionStumpWeakClassifier{Float64}}([…《略》

julia> length(H2k.alpha)
2000

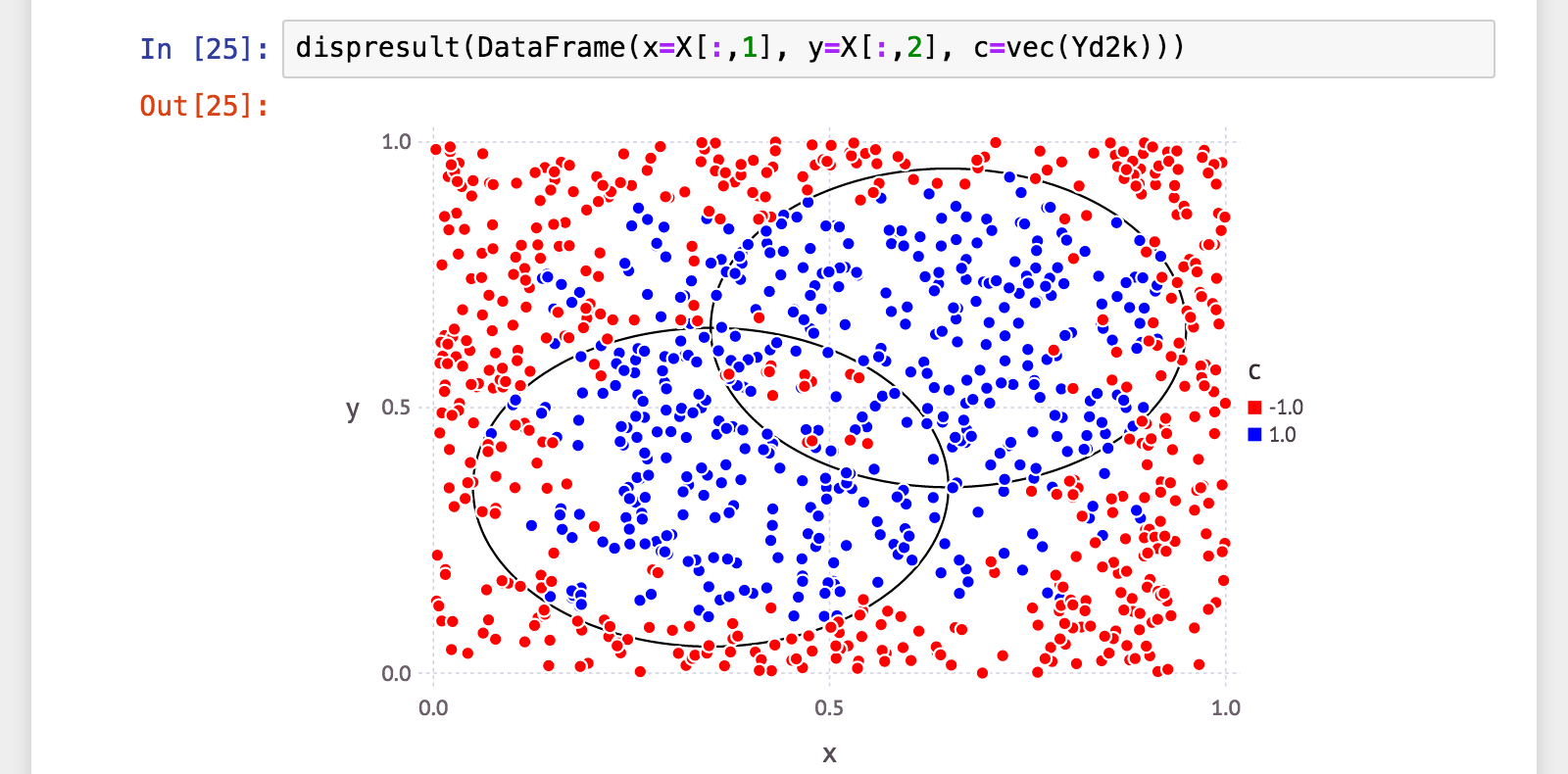
julia> Yd2k = H2k(X);

julia> (a, p, r, f) = calc_mlmetrics(Y, Yd2k);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.851000

julia> @printf("precision: %.06f\n", p)
precision: 0.812095

julia> @printf("recall: %.06f\n", r)
recall: 0.858447

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.834628

julia> x_test = rand(100, 2);

julia> y_test = H2k(x_test);

julia> (a, p, r, f) = calc_mlmetrics(makelabels(x_test), y_test);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.750000

julia> @printf("precision: %.06f\n", p)
precision: 0.711111

julia> @printf("recall: %.06f\n", r)
recall: 0.727273

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.719101

微妙に改善…でもまだまだ先は長そうですね＞＜

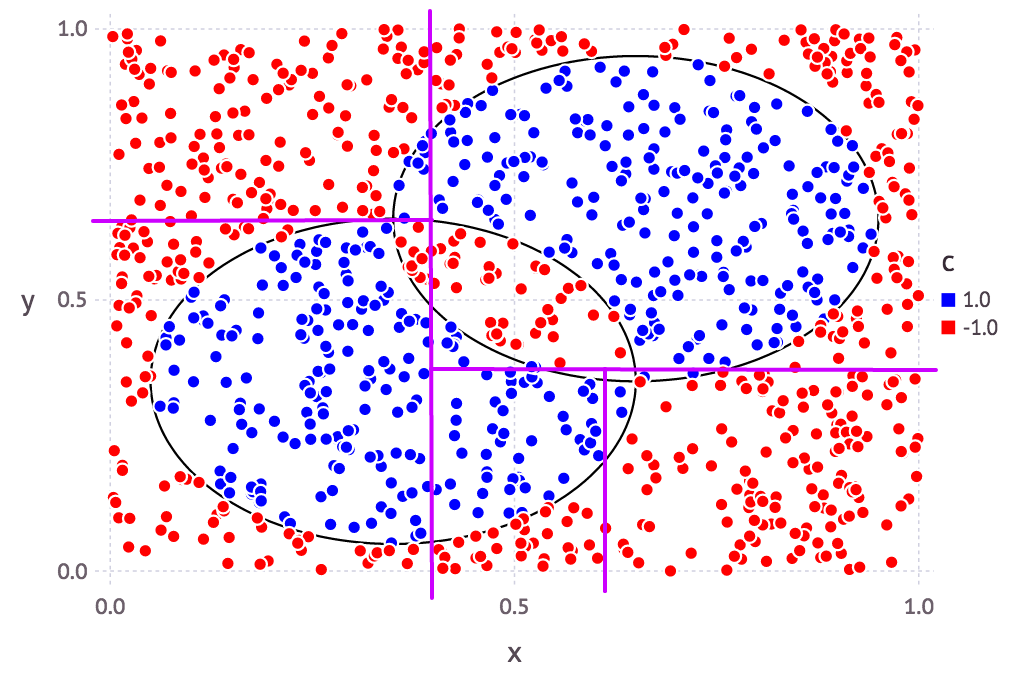
決定株を斜めにしてみた。

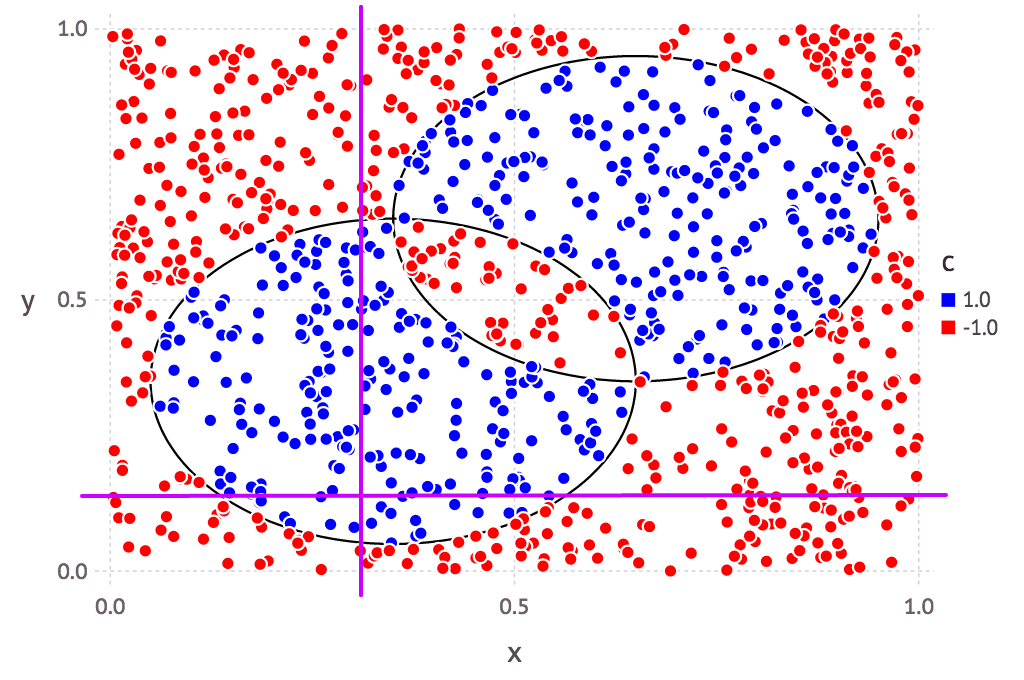
そもそも決定株というのは、複数ある説明変数（軸）のうち、どれか1つのみに注目して、最適に分類できてそうな境界を探るもの。
今回のサンプルデータで見てみると、例えばこんな感じ（あくまでイメージです）：

つまり説明変数が2個（＝2軸）の場合、平面上のx軸かy軸か、どちらかしか基準がない、とも言えます。
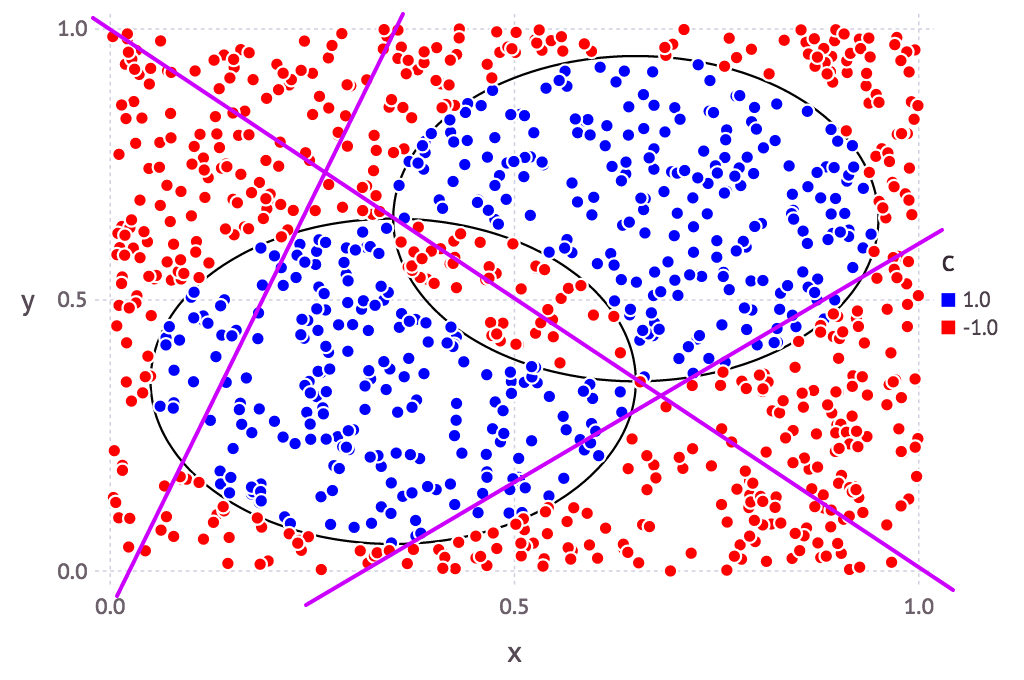
これ、斜めにしたらどうだろう？ついでにその傾きを毎回ランダムに決定したらなんか良くね？（イメージ：）

と、思いつきまして、試してみました。

斜めの決定株（Beveled Decision Stump）の実装

実装はこんな感じ：

beveleddecisionstumpweakclassifier.jl

immutable BeveledDecisionStumpWeakClassifier{T<:AbstractFloat} <: WeakClassifier{T}
    w::AbstractArray{T, 1}
    b::T
end

function weaklearn{T<:AbstractFloat}(
        ::Type{BeveledDecisionStumpWeakClassifier},
        X::AbstractMatrix{T},
        Y::AbstractVector{T},
        D::AbstractVector{T})
    # @assert size(X)[1] == length(Y) == length(D)
    (N, M) = size(X)
    W0 = rand(T, M) .* 2 .- 1
    Xs = X * W0
    xi = sortperm(Xs)
    WY = Y .* D
    el = cumsum(WY[xi])
    eu = cumsum(WY[reverse(xi)])
    es = eu[end-1:-1:1] .- el[1:end-1]
    idx = indmax(abs(es))
    d = sign(es[idx])
    w = d .* W0
    b = -0.5d * (Xs[xi[idx]] + Xs[xi[idx+1]])
    BeveledDecisionStumpWeakClassifier(w, b)
end
@inline weaklearn(::Type{BeveledDecisionStumpWeakClassifier}, X, Y, D; kwds...) = 
    weaklearn(BeveledDecisionStumpWeakClassifier, X, Y, D)

function (h::BeveledDecisionStumpWeakClassifier{T}){T}(x::AbstractMatrix{T})
    _signplus(x * h.w .+ h.b)
end

function (h::BeveledDecisionStumpWeakClassifier{T}){T}(x::AbstractVector{T})
    _signplus(dot(x, h.w) + h.b)
end

学習は、軸を乱択する代わりに、境界平面（2次元の場合は境界線。M次元の場合はM-1次元超平面）の傾きを決定するM個の係数を乱択。それを元のX（N行M列の行列）と積を取ることでN次元のベクトルを算出（各点のその（超）平面からの符号付距離が入る）。あとは普通の Decision Stump と同じ。
分類は、そうしてできた（超）平面の多項式に各変数を代入して正か負か（＝平面のどっち側か）を見るだけ（平面上の場合は正と判定）。

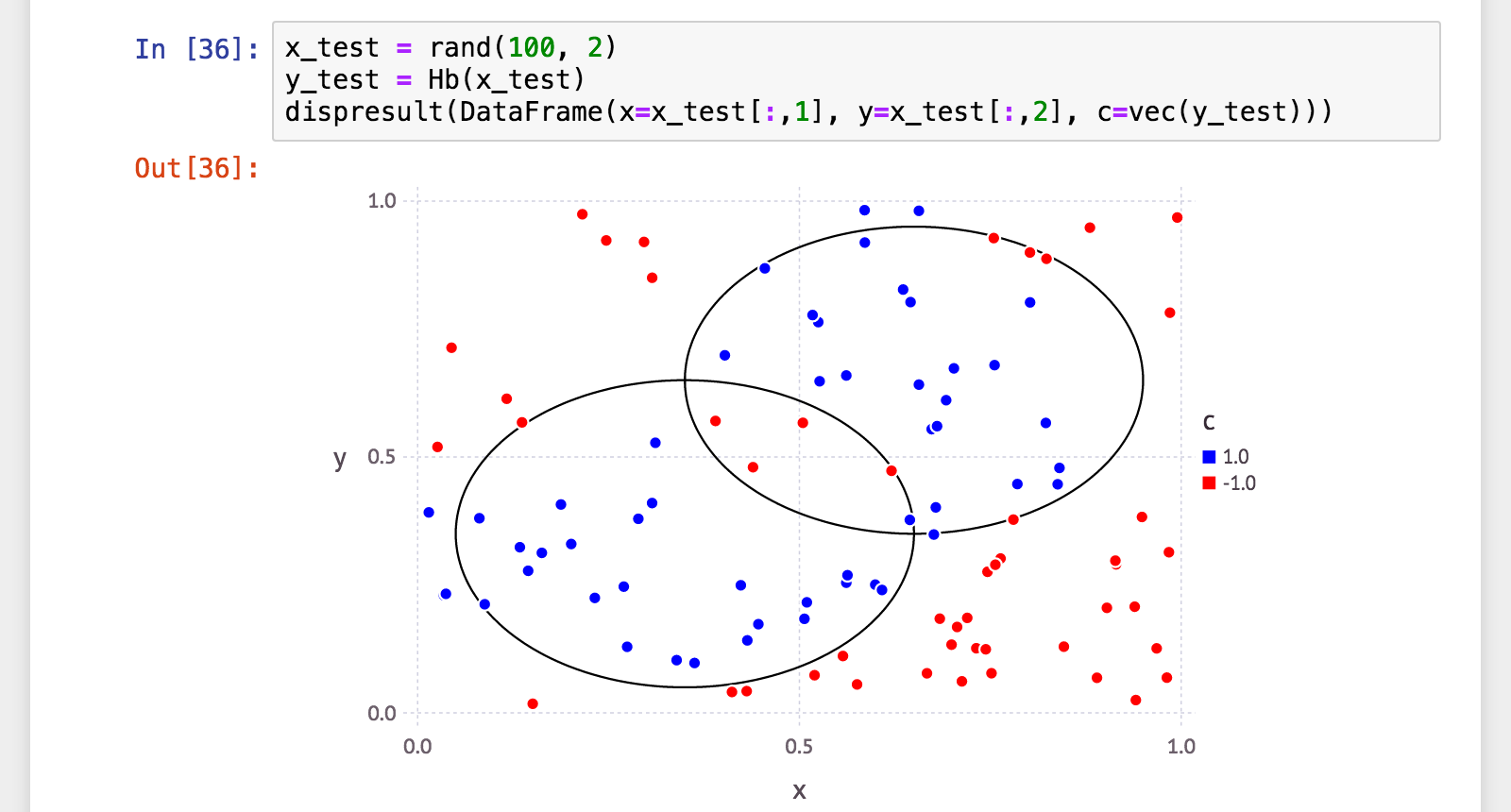
t=100

学習・分類してみました。まずは弱学習器100個から。

julia> include("beveleddecisionstumpweakclassifier.jl")

julia> Hb = adaboost(X, Y; t=100, wc=BeveledDecisionStumpWeakClassifier)
AdaBoost{Float64,BeveledDecisionStumpWeakClassifier{Float64}}([…《略》

julia> length(Hb.alpha)
100

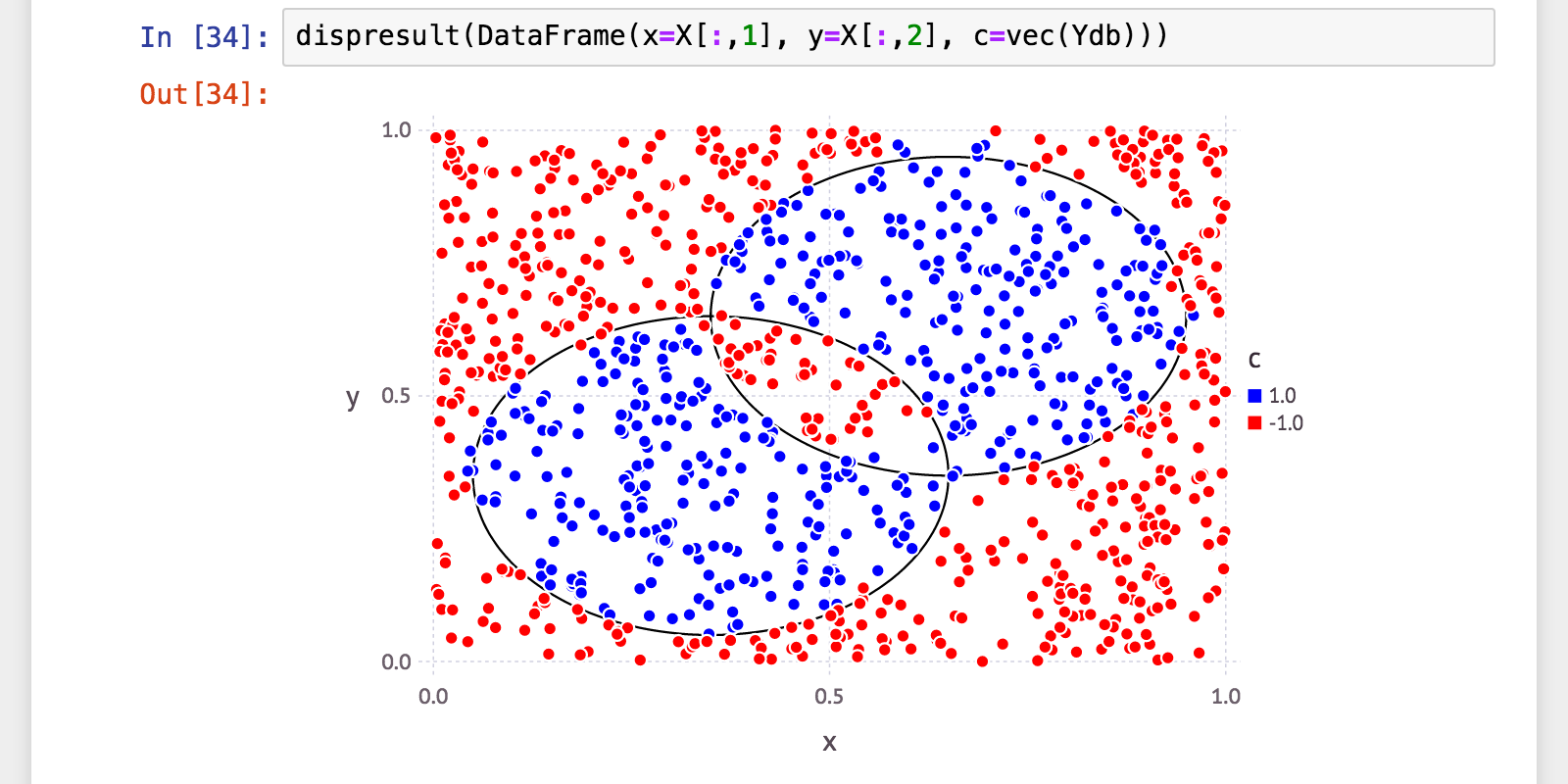
julia> Ydb = Hb(X);

julia> (a, p, r, f) = calc_mlmetrics(Y, Ydb);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.982000

julia> @printf("precision: %.06f\n", p)
precision: 0.970852

julia> @printf("recall: %.06f\n", r)
recall: 0.988584

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.979638

びっくりするくらい性能が上がりました！
汎化性能も見てみましょう。

julia> x_test = rand(100, 2);

julia> y_test = Hb(x_test);

julia> (a, p, r, f) = calc_mlmetrics(makelabels(x_test), y_test);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.900000

julia> @printf("precision: %.06f\n", p)
precision: 0.865385

julia> @printf("recall: %.06f\n", r)
recall: 0.937500

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.900000

なかなかいい感じ。

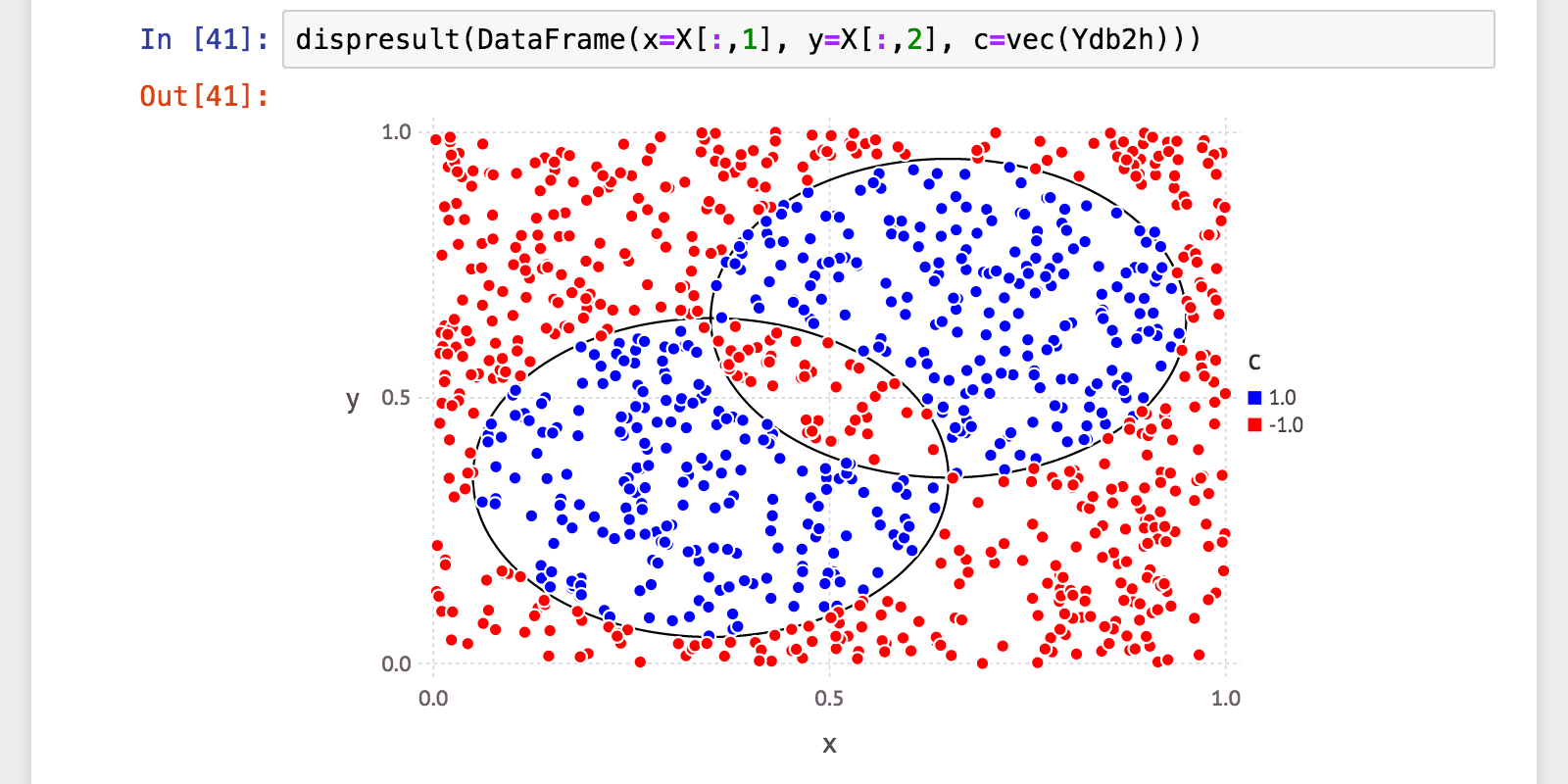
t=200

最大200個まで増やしてみました。

julia> Hb2h = adaboost(X, Y; t=200, wc=BeveledDecisionStumpWeakClassifier)
AdaBoost{Float64,BeveledDecisionStumpWeakClassifier{Float64}}([…《略》

julia> length(Hb.alpha)
200

julia> Ydb2h = Hb2h(X);

julia> (a, p, r, f) = calc_mlmetrics(Y, Ydb2h);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.998000

julia> @printf("precision: %.06f\n", p)
precision: 0.997717

julia> @printf("recall: %.06f\n", r)
recall: 0.997717

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.997717

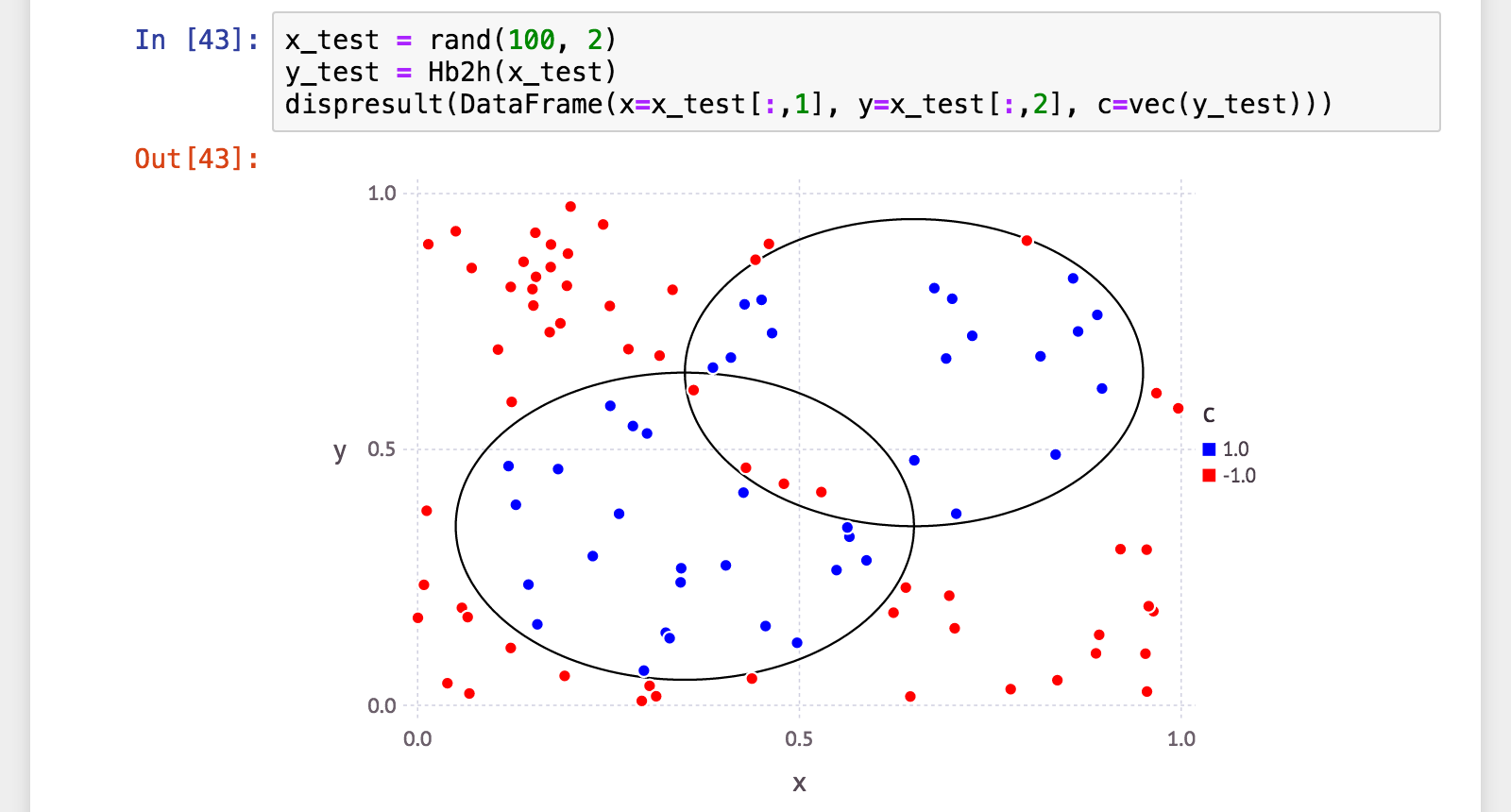
julia> x_test = rand(100, 2);

julia> y_test = Hb2h(x_test);

julia> (a, p, r, f) = calc_mlmetrics(makelabels(x_test), y_test);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.990000

julia> @printf("precision: %.06f\n", p)
precision: 1.000000

julia> @printf("recall: %.06f\n", r)
recall: 0.975610

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.987654

汎化性能、正解率99%、適合率100%（＝誤検出ゼロ）！再現率97.6%（＝検出漏れ2.4%）は少々気になりますけれど。
元の（普通の）決定株に比べて、弱分類器の数は1/5〜1/10。それでこの数値は、なかなか良いじゃないですか。

決定木の場合

やっぱり基本。
決定株を決定木にしてみました。
予想では、精度（少なくとも正解率）はさらに上がるはず。

決定木（Decision Tree）の実装

実装はこんな感じ（ちょっと長くなるので一部省略）：

beveleddecisionstumpweakclassifier.jl(excerpt)

abstract AbstractDTree{T}

type DTreeNode{T} <: AbstractDTree{T}
    val::T
    axis::Int
    b::T
    left::AbstractDTree{T}
    right::AbstractDTree{T}
end

immutable DTreeLeaf{T} <: AbstractDTree{T}
    val::T
end

function applydtree(leafornode, x)
    ; # 《略》
end

immutable DecisionTreeWeakClassifier{T<:AbstractFloat} <: WeakClassifier{T}
    tree::AbstractDTree{T}
end

function builddtree{T}(
        val::T,
        X::AbstractMatrix{T},
        WY::AbstractVector{T},
        depth::Int)
    if depth == 0
        return DTreeLeaf(val)
    elseif length(WY) == 1
        return DTreeLeaf(sign(WY[1]))
    end
    (N, M) = size(X)
    tgtidx = rand(1:M)
    xi = sortperm(X[:,tgtidx])
    el = cumsum(WY[xi])
    eu = cumsum(WY[reverse(xi)])
    es = eu[end-1:-1:1] .- el[1:end-1]
    idx = indmax(abs(es))
    if abs(sum(WY)) > abs(es[idx])
        return DTreeLeaf(sign(sum(WY)))
    end
    d = sign(es[idx])
    b = (X[xi[idx],tgtidx] + X[xi[idx + 1],tgtidx]) / 2
    lidxs = xi[1:idx]
    ridxs = xi[idx+1:end]
    DTreeNode(val, tgtidx, b, 
        builddtree(-d, X[lidxs, :], WY[lidxs], depth-1),
        builddtree(d, X[ridxs, :], WY[ridxs], depth-1))
end

function weaklearn{T<:AbstractFloat}(
        ::Type{DecisionTreeWeakClassifier},
        X::AbstractMatrix{T},
        Y::AbstractVector{T},
        D::AbstractVector{T};
        maxdepth::Int=3,
        kwds...)
    # @assert size(X)[1] == length(Y) == length(D)
    WY = Y .* D
    DecisionTreeWeakClassifier(builddtree(one(T), X, WY, maxdepth))
end

function (h::DecisionTreeWeakClassifier{T}){T}(x::AbstractVecOrMat{T})
    applydtree(h.tree, x)
end

weaklearn() 関数にオプション引数 maxdepth を追加しています。木の深さの最大値です。デフォルト値は 3 にしました。
学習は、決定株を多層にしただけ。簡単ですね。

t=100, maxdepth=3

学習・分類。弱学習器100個、深さはデフォルト値の3。

julia> include("decisiontreeweakclassifier.jl")

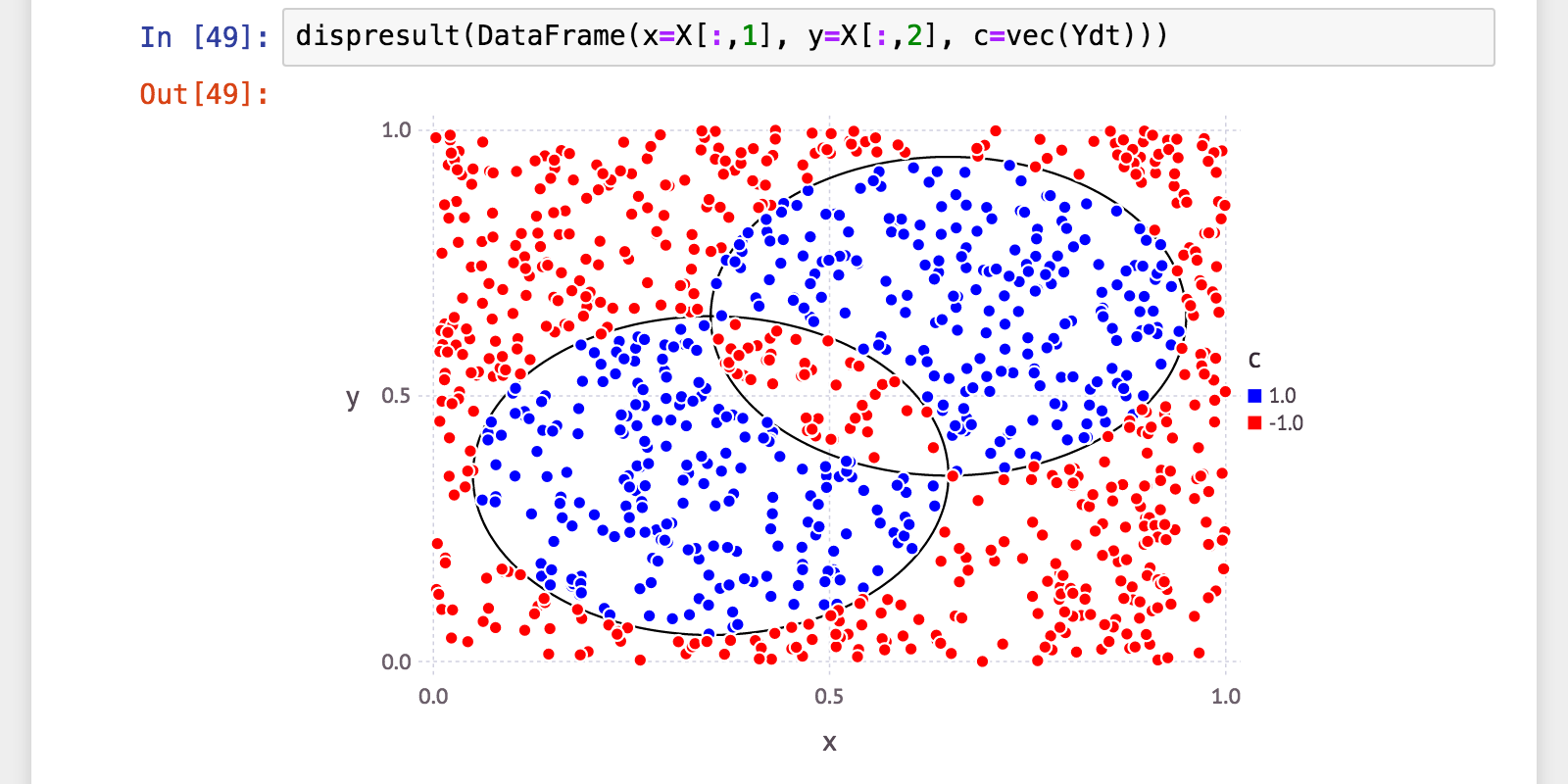
julia> Ht = adaboost(X, Y; t=100, wc=DecisionTreeWeakClassifier)
AdaBoost{Float64,DecisionTreeWeakClassifier{Float64}}([…《略》

julia> length(Ht.alpha)
100

julia> Ydt = Ht(X);

julia> (a, p, r, f) = calc_mlmetrics(Y, Ydt);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 1.000000

julia> @printf("precision: %.06f\n", p)
precision: 1.000000

julia> @printf("recall: %.06f\n", r)
recall: 1.000000

julia> @printf("f_measure: %.06f\n", f)
f_measure: 1.000000

予想通り高性能！正答率・F-値100%！
ただこうなると過学習が心配ですね…ということで、汎化性能。

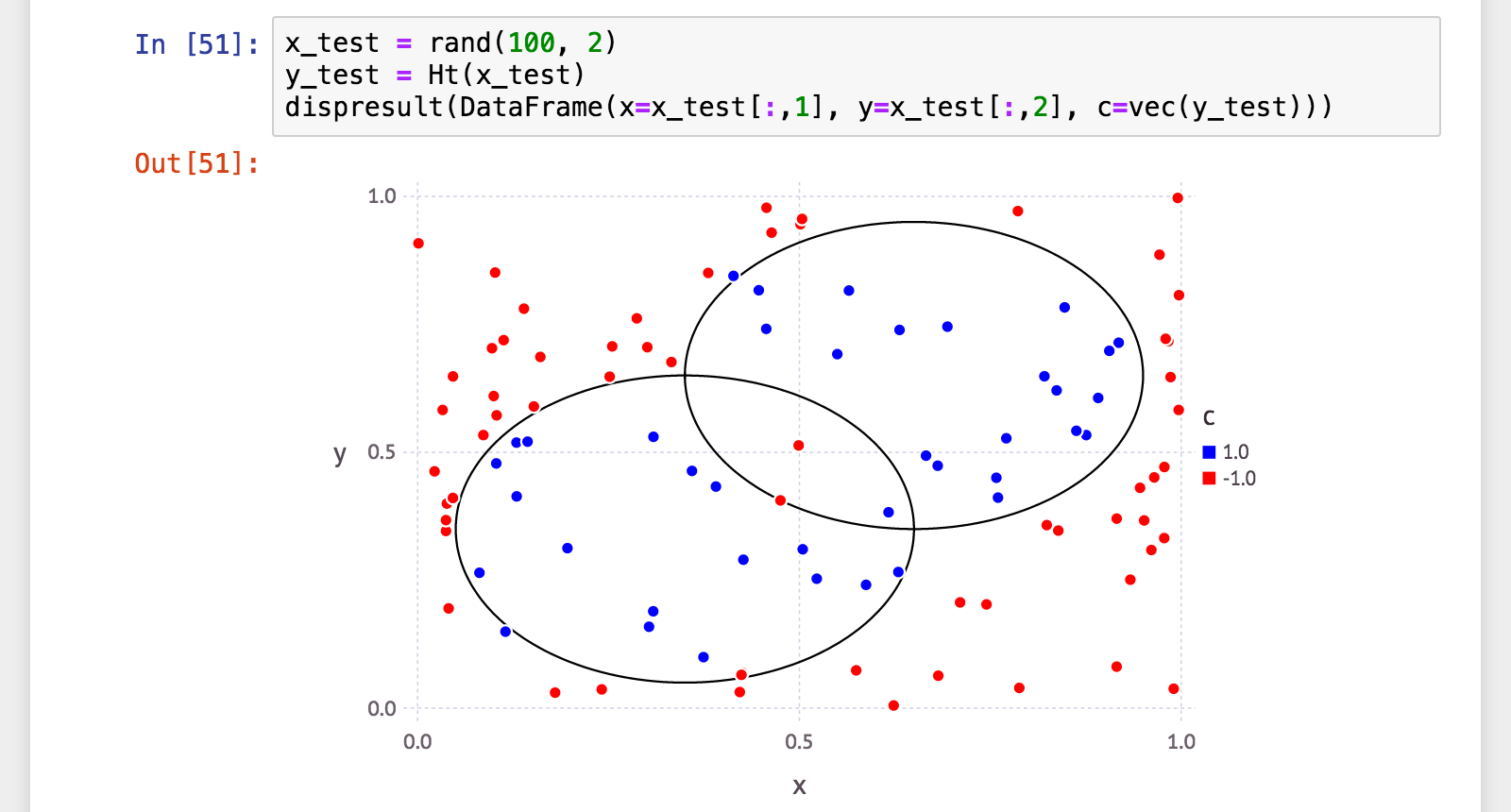
julia> x_test = rand(100, 2);

julia> y_test = Ht(x_test);

julia> (a, p, r, f) = calc_mlmetrics(makelabels(x_test), y_test);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.940000

julia> @printf("precision: %.06f\n", p)
precision: 0.923077

julia> @printf("recall: %.06f\n", r)
recall: 0.923077

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.923077

うん、やっぱり多少過学習ぎみ。それでもこの数値ならかなり良さげですね。

t=100, maxdepth=2

maxdepth=3 で思いの外高性能（ただし過学習気味）だったので、弱学習器の数は変えずにmaxdepth=2 にして試してみました。

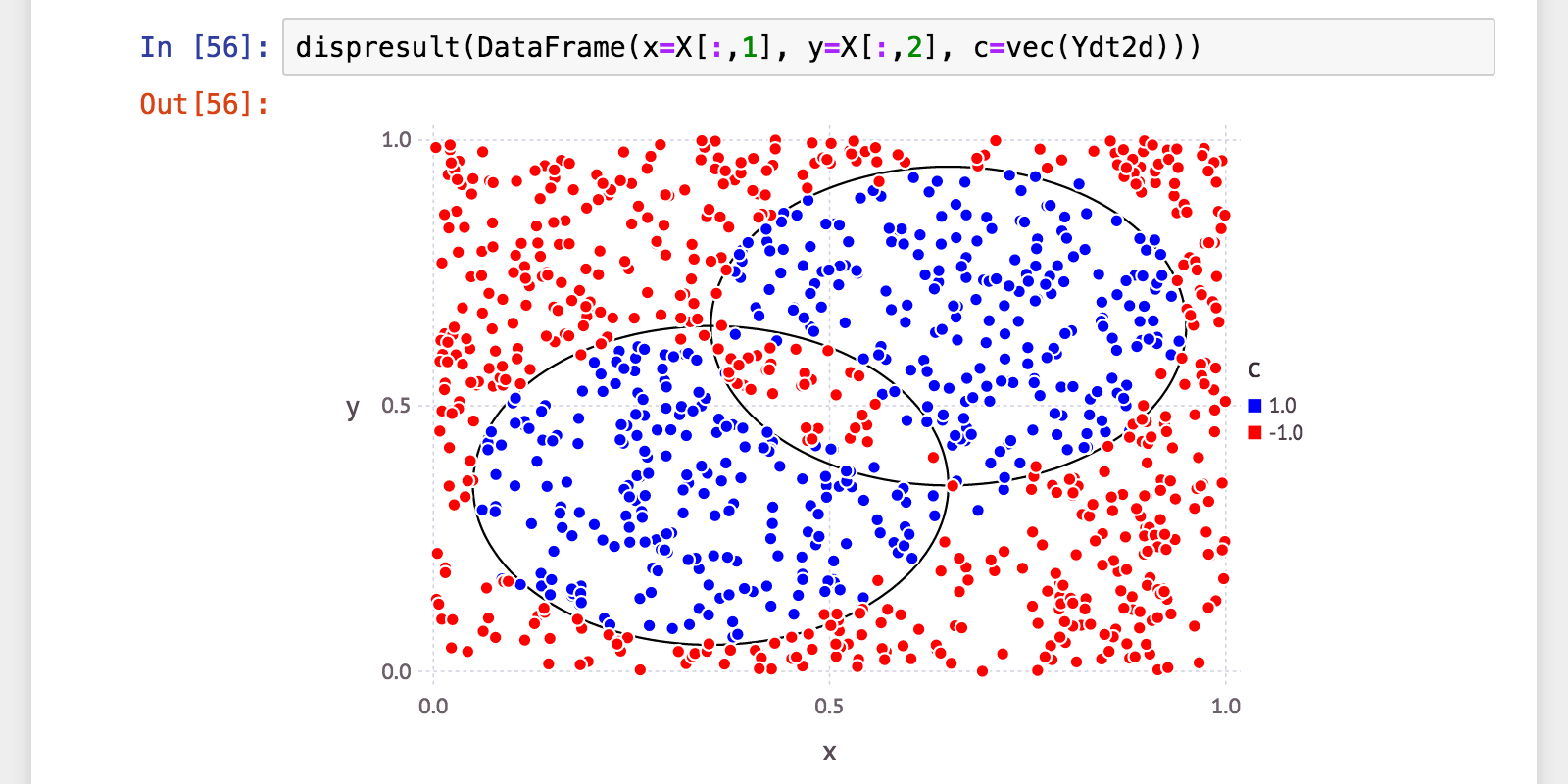
julia> Ht2d = adaboost(X, Y; t=100, wc=DecisionTreeWeakClassifier, maxdepth=2)
AdaBoost{Float64,DecisionTreeWeakClassifier{Float64}}([…《略》

julia> length(Ht2d.alpha)
100

julia> Ydt2d = Ht2d(X);

julia> (a, p, r, f) = calc_mlmetrics(Y, Ydt2d);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.966000

julia> @printf("precision: %.06f\n", p)
precision: 0.957014

julia> @printf("recall: %.06f\n", r)
recall: 0.965753

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.961364

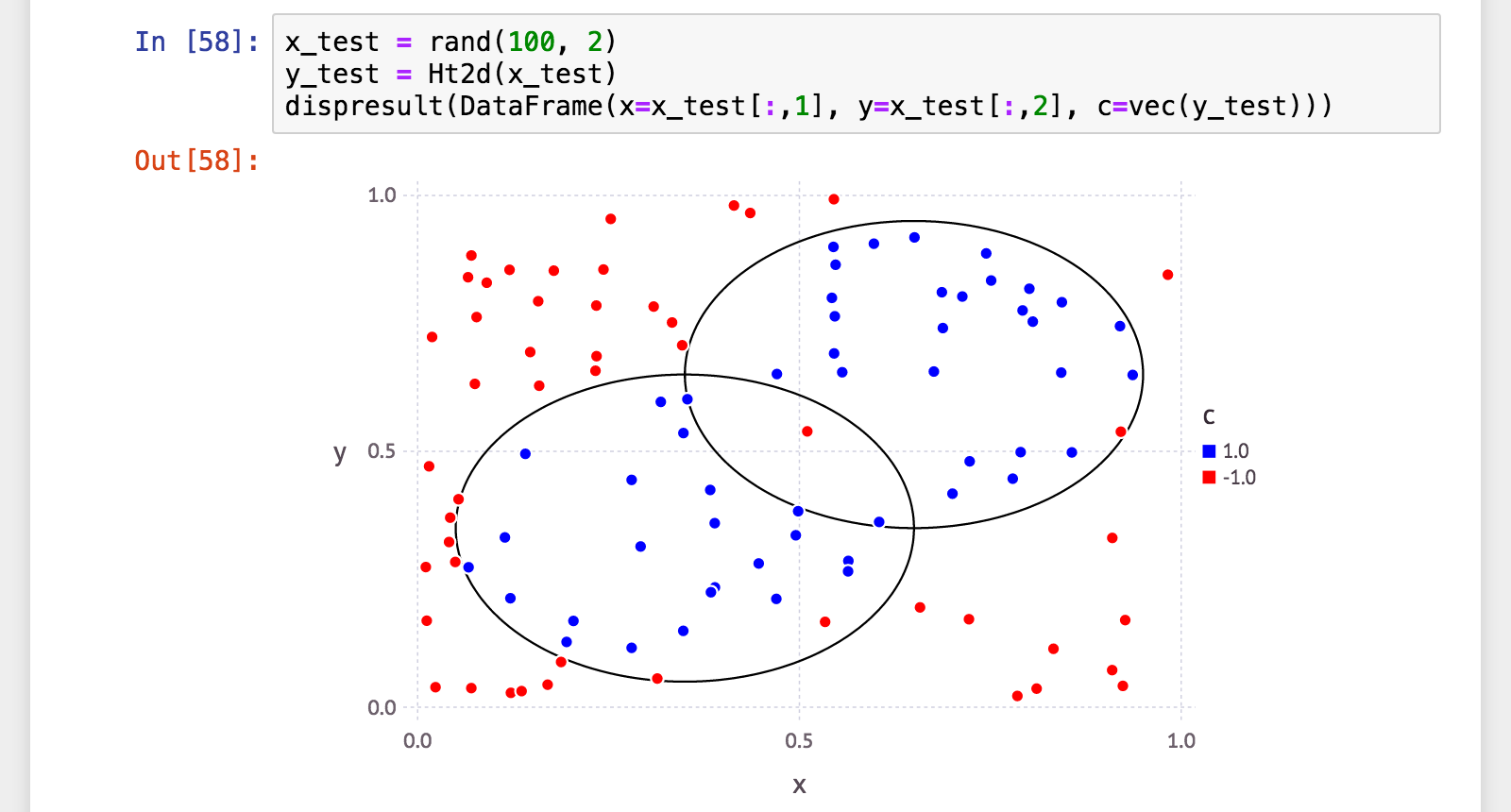
julia> x_test = rand(100, 2);

julia> y_test = Ht2d(x_test);

julia> (a, p, r, f) = calc_mlmetrics(makelabels(x_test), y_test);

julia> @printf("accuracy: %.06f\n", a)
accuracy: 0.960000

julia> @printf("precision: %.06f\n", p)
precision: 0.980392

julia> @printf("recall: %.06f\n", r)
recall: 0.943396

julia> @printf("f_measure: %.06f\n", f)
f_measure: 0.961538

訓練性能は少し落ちましたが、汎化性能は寧ろ向上。またどちらもほぼ同じ数値、バランスは取れています。

速度評価

それぞれの学習および分類の時間を計測してみました。

学習時間

julia> Base.gc(true); @time adaboost(X, Y; t=1000);
  0.173937 seconds (59.16 k allocations: 179.057 MB, 22.12% gc time)

julia> Base.gc(true); @time adaboost(X, Y; t=2000);
  0.324151 seconds (118.03 k allocations: 358.083 MB, 16.43% gc time)

julia> Base.gc(true); @time adaboost(X, Y; t=100, wc=BeveledDecisionStumpWeakClassifier);
  0.013637 seconds (6.42 k allocations: 17.183 MB)

julia> Base.gc(true); @time adaboost(X, Y; t=200, wc=BeveledDecisionStumpWeakClassifier);
  0.030205 seconds (12.82 k allocations: 34.350 MB, 11.57% gc time)

julia> Base.gc(true); @time adaboost(X, Y; t=100, wc=DecisionTreeWeakClassifier);
  0.050829 seconds (42.65 k allocations: 46.169 MB, 15.03% gc time)

julia> Base.gc(true); @time adaboost(X, Y; t=100, wc=DecisionTreeWeakClassifier, maxdepth=2);
  0.059504 seconds (20.55 k allocations: 31.923 MB, 13.18% gc time)

分かりやすいですね。弱分類器の数にほぼ比例しています。

分類時間

julia> Base.gc(true); @time H(X);
  0.025561 seconds (14.54 k allocations: 8.029 MB)

julia> Base.gc(true); @time H2k(X);
  0.029515 seconds (14.54 k allocations: 15.659 MB)

julia> Base.gc(true); @time Hb(X);
  0.028651 seconds (415.54 k allocations: 7.251 MB)

julia> Base.gc(true); @time Hb2h(X);
  0.038001 seconds (815.54 k allocations: 14.224 MB)

julia> Base.gc(true); @time Ht(X);
  0.032033 seconds (341.59 k allocations: 6.123 MB)

julia> Base.gc(true); @time Ht2d(X);
  0.037214 seconds (255.19 k allocations: 4.804 MB)

構造が複雑になるほど時間がかかりますが、「同じ性能（正解率）を出す分類器の分類にかかる時間」と考えると、「斜めの決定株」が割と優秀な気がします。

ここまでのまとめ

表にしてみました。
以下、DS: 決定株、BS: 斜めの決定株、DT: 決定木。

弱学習器およびパラメータ	訓練性能（正解率）	汎化性能（正解率）	学習時間(s)	分類時間(s)
DS, t=1000	81.7%	72.0%	0.173937	0.025561
DS, t=2000	85.1%	75.0%	0.324151	0.029515
BS, t=100	98.2%	90.0%	0.013637	0.028651
BS, t=200	99.8%	99.0%	0.030205	0.038001
DT, t=100, maxdepth=3	100.0%	94.0%	0.050829	0.032033
DT, t=100, maxdepth=2	96.6%	96.0%	0.059504	0.037214

学習時間と安定した精度を求めるなら、「斜めの決定株（t=200）」。
分類速度とある程度の精度を求めるなら、「決定木（d=3）」。
と言ったところでしょうか。

なお、何度か実行してみましたが大体同じ結果になりました、ということを付言しておきます。

他の分類データ

今回の分類データがあまりに特殊すぎたかもしれない、と思い、少し違うデータでも試してみました。
結果だけ示します。

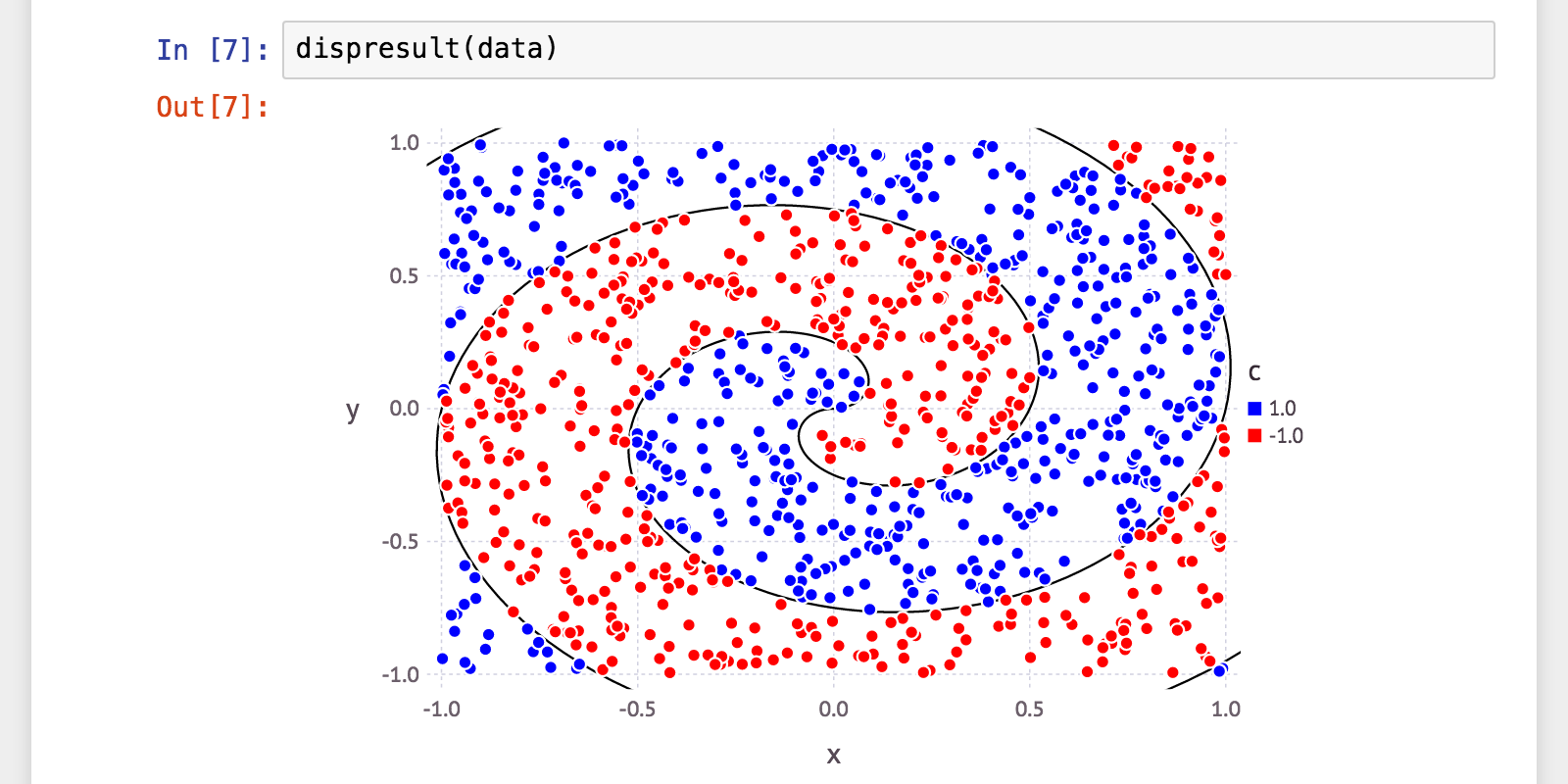
ぐるぐる（アルキメデス螺旋ベース）

弱学習器およびパラメータ	訓練性能（正解率）	汎化性能（正解率）	学習時間(s)	分類時間(s)
DS, t=1000	80.1%	70.0%	0.155572	0.135507
DS, t=2000	82.2%	69.0%	0.427481	0.088738
BS, t=100	97.8%	94.0%	0.020341	0.101591
BS, t=200	99.0%	95.0%	0.032742	0.126774
DT, t=100, maxdepth=3	99.6%	95.0%	0.065813	0.102042
DT, t=100, maxdepth=2	95.0%	94.0%	0.034316	0.061358

傾向としては、2つの円の時とほぼ同じ感じ。全体的に精度は落ちました。

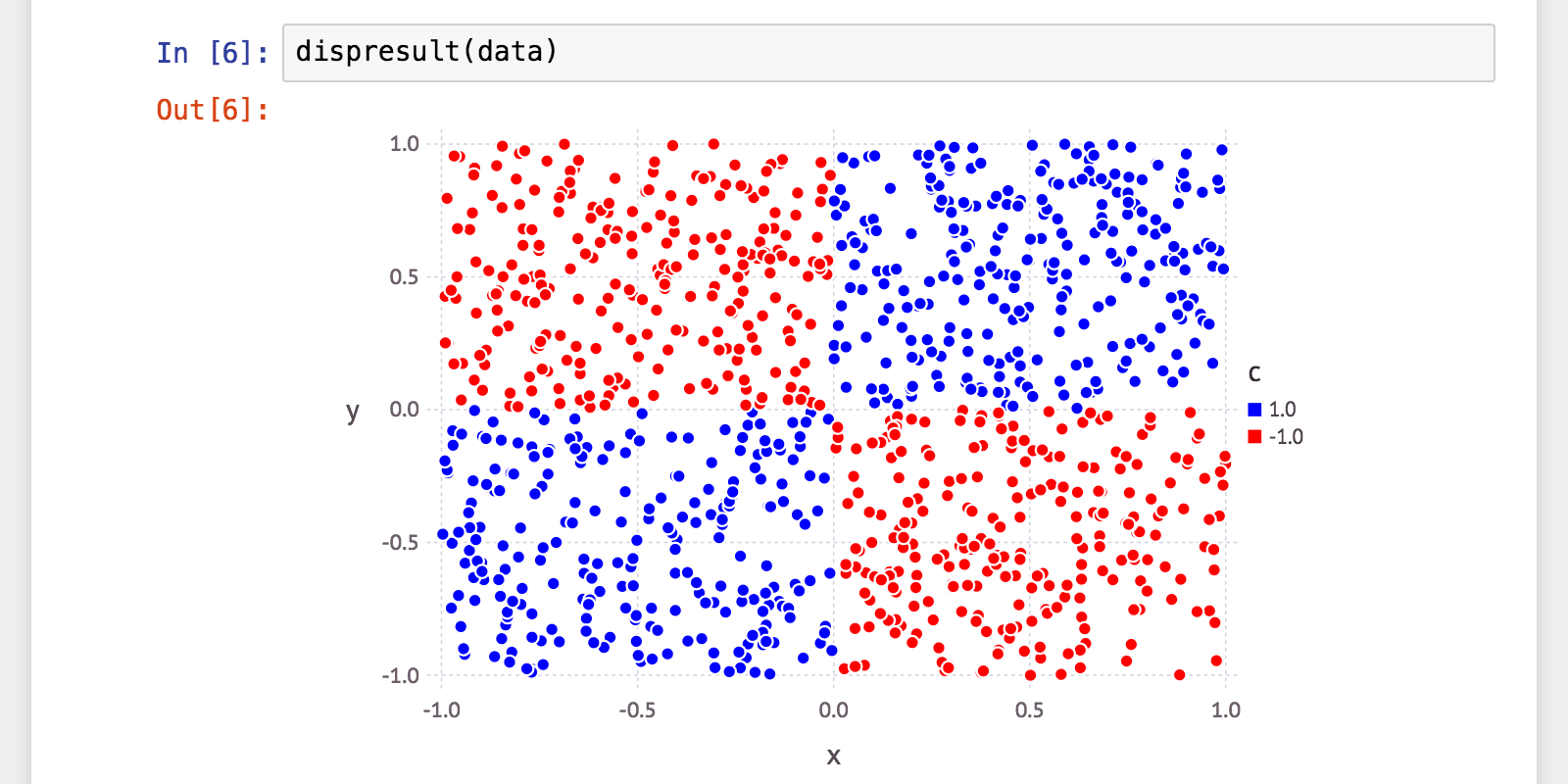
シンプル

弱学習器およびパラメータ	訓練性能（正解率）	汎化性能（正解率）	学習時間(s)	分類時間(s)
DS, t=1000	70.7%	49.0%	0.164527	0.022333
DS, t=2000	73.9%	52.0%	0.278538	0.031139
BS, t=100	100.0%	100.0%	0.013001	0.026756
BS, t=200	100.0%	99.0%	0.029818	0.036352
DT, t=100, maxdepth=3	49.6%	55.0%	0.037481	0.013271
DT, t=100, maxdepth=2	100.0%	100.0%	0.038498	0.028926

決定木を利用したものに少しおかしな結果が。データが余りにもキレイに別れている分、Treeがうまく構築できなかった模様。これは少し実装を見直した方が良いかも。
それにつけても「斜めの決定株」の安定していることよ。なぜ斜めにしただけでこのデータで100%たたき出すのか逆に不思議。

考察

「斜めの決定株」がここまで高い性能を示したのには、一つにはやはり、データの特殊性もきっとあるとは思います。
少なくとも、落ち着いて考えるとどれも、各説明変数の値域も分散も同じですから。
それをもっと崩したデータで試したら、もう少し結果が変わってくるかもしれません。

「決定木」の方は、実装次第かもしれませんが、基本的には低バイアス高バリアンスなので、バイアスを弱めるブースティングにはあまり向かないのかな、と。なのでせいぜい深さ3までで試してみたのですが、それでも過学習気味になる傾向が出ました。

あと今回は AdaBoost で試しましたが、「斜めの決定株」を決定木の各Nodeに採用したり、それを利用した RandomForest を構築したらどうなるんだろう？などなど、時間があれば引き続き少しずつ実験を重ねていこうかな、と思っています。

最後に

今回実験したコード・データ等は、Gist に上げておきました。→ AdaBoostSample.ipynb （nbviewer による .ipynb ファイル表示： AdaBoostSample.ipynb、AdaBoostSample2.ipynb、AdaBoostSample3.ipynb）
省略したコードも全て載せてますし、追加の実験等もありますので見てみてください。よろしければご意見いただければと思います。

あと、最後に上げる参考文献（書籍）以外、論文等は全然参照してません（思いつきで実験しただけ）なので、「すでにこんな論文あるよ」等の情報もありましたらどなたかお願いします。

そもそも思いつきで仮で「斜めの決定株（Beveled Decision Stump）」なんて造語しましたが、もし既に知られていて正式名称とかあれば…(^-^;

明日は、 @awakia さんによる記事の予定です。お楽しみに！

参考文献

パターン認識と機械学習下丸善出版
イラストで学ぶ機械学習最小二乗法による識別モデル学習を中心に講談社

というか実際、今ひとつ性能が上がらなくて試しで弱学習器を少し弄ったら劇的に性能が上がったりしました。それがこの記事を書こうと思ったきっかけです。 ↩
個人の感想です。 ↩
Julia の言語仕様とかは、本家サイトのドキュメントや Julia Advent Calendar の各記事とかを参照してください。ここでは詳解は省きます。やってることは大体読み取れると思います。 ↩
_signplus() 関数は所謂階段関数。sign() 関数は Julia にも標準で存在しますけれど、sign(0.0) == 0.0 となってしまうのでそれを回避するために用意。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up