スクフェス問題
ある日、次のような問題を見つけました。
・ラブカストーンは1個60円とします。
・ラブカストーン5個で一回ガチャが出来ます。
・ガチャで1%の確率でURランクのカードが出ます。
・URランクのカードは100種類あります。
・100種類の内、どれでもいいのですが、9種類のURランクのカードで、全く同じカードが二枚必要です。上記の条件を達成するために、お金が何円必要でしょう?
分かる人は分かると思いますが、これはライブライブで最強ユニットを組むために必要な金額です。
スクフェスというゲームにおいて、ごく単純な仮定の下でガチャのみで最強ユニット(通称覚醒UR艦隊)を組むのにどれくらいの金額がかかるのか、を問う問題です。
このゲームでは同一種類のURカード2枚を合成すると覚醒URカードと呼ばれるものを作ることができ、覚醒URカードを9種類集めると最強ユニットを組むことができるので、このような問題の条件となっています。
覚醒UR艦隊を組むのにかかる金額は確率変数となるので、その確率分布を明らかにできればこの問題に完答できたことになります。
そこで、さっそく解いてみることにしました。
※なお、実際のスクフェスでは覚醒UR艦隊を組む際、問題文と異なり同一種類のカードを重複させられるようなのですが、あくまで元の問題文に忠実に、9種類の別々の覚醒URカードで覚醒UR艦隊を作るという問題を解くことにします
回答
計算方法にはそこまで興味が無い人が多いと思うので、答えを先に載せておきます。
(問題の仮定の下では)スクフェスで覚醒UR艦隊を組むには最低5400円、最高で∞円、平均で約1475848円かかります。
1462200円かければ覚醒UR艦隊を組めるか組めないかがほぼ半々になります。
1842300円かければ約90%の確率で覚醒UR艦隊を組むことができます。
結果の詳細です。
以下のグラフは、覚醒UR艦隊を組むのにかかる金額の累積確率分布をグラフで表したものです。
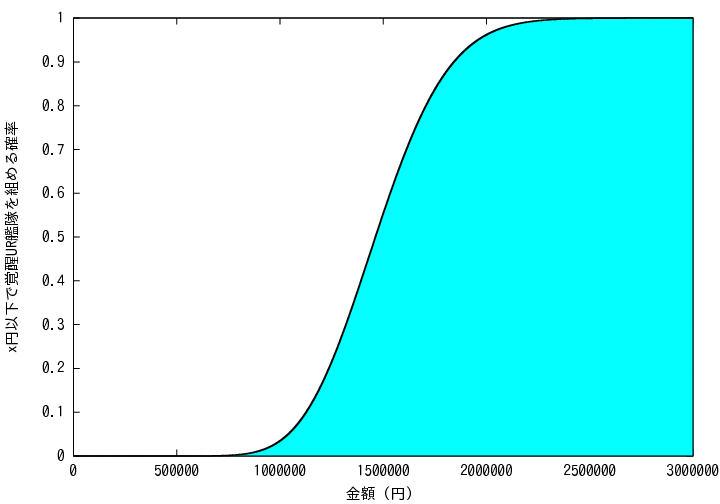
グラフの見方ですが、グラフ上の曲線は、x座標の金額以下で覚醒UR艦隊を組める確率はy座標の値となるという関係を表しています。
例えば、100万円以下の金額で覚醒UR艦隊を組める確率は約3.5%しかありません。
計算方法
まず肩慣らしとして最低金額と最高金額の計算をした後、確率分布の計算について説明します。
平均金額の計算は最も難しいので最後に説明します。
最低金額
最低金額とは、どんなに運が良い人でも覚醒UR艦隊を組むのには最低限これだけの金額は必要になるという金額です。
最低金額の計算は簡単です。
最終的に9種類のURカードが各2枚必要になるので、最低18回ガチャを引く必要があります。
ガチャを1回引くのに300円必要なので、覚醒UR艦隊を組むのに必要な最低金額は300×18=5400円となります。
最高金額
最高金額とは、どんなに運が悪い人でもこれだけの金額をかければ覚醒UR艦隊を組めることが保証されるという金額です。
ガチャに対するよくある誤解に気付いてさえいれば、最高金額の計算も簡単です。
ガチャ1回でURが出る確率は1%なので、100回引けば必ずURが出るはずであり、ガチャを引き続けていればURが溜まっていくからいつかは必ず覚醒UR艦隊を組めるはず、という考えは誤りです。
ガチャを100回引いてURが1回も出ない確率は約36.6%もあります(詳細はコンプガチャだけじゃない!? ガチャに潜む確率の罠 - てっく煮ブログを参照)。
そして、ガチャを1万回引こうが1億回引こうが、URが1回も出ない確率は0にはなりません。
URが1回も出ない可能性がある以上、有限の金額では覚醒UR艦隊を組めない確率は0にはできません。
したがって、これだけかければ覚醒UR艦隊を組めると保証できる金額は存在しません。
この事実を(数学の用語に対する厳密さは脇に置いておいて)端的に表現すると、最高金額は∞円であるということになります。
確率分布
覚醒UR艦隊を組むのにx円かかる確率はyであると言えるようになれば、確率分布を明らかにできたことになります。
最低金額と最高金額の計算は簡単ですが、確率分布の計算は難しめの問題です。
自分は確率決定性有限オートマトンを用いる解法を考えました。
用語はいかついのですが、アイデア自体は単純なものです。

まず初期状態として(0, 0)というものを考えます。
左の数字はURを1枚だけ持っているカードが何種類あるかを表し、右の数字はURを2枚以上持っているカードが何種類あるかを表しています。
最初はURカードを1枚も持っていないので、初期状態は(0, 0)となります。

ガチャを1回引くことで状態の遷移が起こると考えます。
99/100=0.99の確率で(0, 0)から(0, 0)に遷移し(つまり元のままです)、1/100=0.01の確率で(1, 0)に遷移することになります。

(1, 0)からは(1, 0)、(2, 0)、(0, 1)のいずれかに遷移することになります。
UR以外が出る確率は99/100なので、(1, 0)への遷移確率は99/100=0.99です。
URが出る確率は1/100で、URが出たときにまだ持っていないURが出る確率は99/100なので、(2, 0)への遷移確率は1/100×99/100=0.0099です。
URが出る確率は1/100で、URが出たときに既に持っているURがまた出る確率は1/100なので、(0, 1)への遷移確率は1/100×1/100=0.0001です。

(0, 1)からは(0, 1)、(1, 1)のいずれかに遷移することになります。
UR以外が出る確率は99/100で、3枚目のURが出てURが無駄になる確率は1/100×1/100なので、(0, 1)への遷移確率は99/100+1/100×1/100=0.9901です。
まだ持っていないURが出る確率は1/100×99/100なので、(1, 1)への遷移確率は1/100×99/100=0.0099です。

このようにしていくと、URカード収集状況の状態遷移図を描くことができます。(クリックで拡大)

最終的に目指すべきゴールは、状態遷移図の最下部にある(n, 9)です。
これはURを2枚以上持っているカードが9種類あることを表す状態です(URを1枚だけ持っているカードは何種類あってもいい)。
この確率決定性有限オートマトンを用いることで、ガチャをx'回引いた時点で覚醒UR艦隊を組める確率を求められます。
その確率は、(0, 0)から(n, 9)への経路のうち経路長x'のものを全て列挙し、それらの経路を通る確率を全て足し合わせたものです。
これで、x=300x'とおくと、覚醒UR艦隊を組むのにx円かかる確率はyであるということが言えるようになりました。
確率の計算ですがこれは人力では厳しいので、Rubyでプログラムを書きました。
覚醒UR艦隊を組むのにx円かかる確率はcost_dist.prob_at(x)で求めることができます。
class DiscreteProbabilityDistribution
attr_reader :domain
def initialize(domain, &calc)
raise ArgumentError.new("block not given") if calc.nil?
@domain = domain
@calc = calc
@prob_at_cache = {}
end
def prob_at(x)
return 0 unless @domain.include?(x)
return @prob_at_cache[x] if @prob_at_cache.has_key?(x)
@prob_at_cache[x] = @calc.call(x)
end
def *(integer)
DiscreteProbabilityDistribution.new(@domain.min * integer .. @domain.max * integer) {|x|
x % integer == 0 ? prob_at(x / integer) : 0
}
end
end
module ProbabilisticDFA
class Edge
attr_reader :probability, :to
def initialize(probability, to)
@probability = probability
@to = to
end
end
class Node
attr_reader :edges, :hop_count_dist
def initialize
@edges = []
@hop_count_dist = DiscreteProbabilityDistribution.new(1 .. Float::INFINITY) {|x|
@edges.collect {|edge| edge.probability * edge.to.hop_count_dist.prob_at(x - 1)}.inject(0, :+)
}
end
end
class AcceptStateNode
attr_reader :hop_count_dist
def initialize
@hop_count_dist = DiscreteProbabilityDistribution.new(0 .. 0) {|x| 1}
end
end
end
gacha_states = {}
accept_state_node = ProbabilisticDFA::AcceptStateNode.new
(0 .. 100 - 9).each do |n|
gacha_states[[n, 9]] = accept_state_node
end
(0 .. 8).each do |m|
(0 .. 100 - m).each do |n|
gacha_states[[n, m]] = ProbabilisticDFA::Node.new
end
end
(0 .. 8).each do |m|
(0 .. 100 - m).each do |n|
gacha_states.fetch([n, m]).edges << ProbabilisticDFA::Edge.new((9900 + m) / 10000.0, gacha_states.fetch([n, m]))
gacha_states.fetch([n, m]).edges << ProbabilisticDFA::Edge.new((100 - (n + m)) / 10000.0, gacha_states.fetch([n + 1, m])) if n + m < 100
gacha_states.fetch([n, m]).edges << ProbabilisticDFA::Edge.new(n / 10000.0, gacha_states.fetch([n - 1, m + 1])) if n > 0
end
end
cost_dist = gacha_states.fetch([0, 0]).hop_count_dist * 300
確率分布が求まれば累積確率分布も(0 .. x).collect {|each_x| cost_dist.prob_at(each_x)}.inject(:+)のようにして求まります。
確率分布をそのまま載せるよりも累積確率分布の形に直した方が分かりやすいので、累積確率分布を求めてグラフ化することで先程の図を作りました。
平均金額
平均金額の計算は最難関です。
先程求めた確率分布を持つ確率変数$X$の期待値を求めればよいのですが、今回は確率変数$X$が$x$をとる確率$P(X=x)$を単純な式の形で求められなかったため、期待値の公式$\sum_{x=0}^\infty x \cdot P(X=x)$は使えません。
ともかく(0, 0)から(n, 9)までの平均遷移数が分かればいいので、まずは簡単な部分問題から解いていきます。
次のような状況を考えます。

状態$s_0$は$s_0, s_1, \ldots, s_m$に遷移する可能性があり、それぞれへの遷移確率は$p_0, p_1, \ldots, p_m$とします。
そして、$s_1$〜$s_m$までの各状態は、自分の状態から(n, 9)までの平均遷移数$e_1, e_2, \ldots, e_m$を既に知っているとします。
このとき、$s_0$から(n, 9)までの平均遷移数$e_0$はいくつになるでしょうか?
ひとまず、$e_0$は次のような式で表せます。
e_0=\sum_{l=0}^\infty \sum_{k=1}^m p_0^l p_k (e_k+1+l)
この式は、可能な経路を全列挙し、各径路についてその経路を通る確率×その経路を通った時の(n, 9)までの平均遷移数を求め、それらを足し合わせた値が$e_0$であることを示しています。
先程の式に変形を加えていき、$e_0$の値を求められるように無限が現れない形にします。
\begin{align}
e_0&=\sum_{l=0}^\infty \sum_{k=1}^m p_0^l p_k (e_k+1+l)\\
&=\sum_{l=0}^\infty p_0^l \left(\sum_{k=1}^m p_k (e_k+1+l)\right)\\
&=\sum_{l=0}^\infty p_0^l \left(\sum_{k=1}^m p_k e_k + \sum_{k=1}^m p_k + l \sum_{k=1}^m p_k\right)\\
&=\sum_{l=0}^\infty p_0^l \left(\sum_{k=1}^m p_k e_k + (1 - p_0) + l (1 - p_0)\right)\\
&=\sum_{l=0}^\infty p_0^l \left(\sum_{k=1}^m p_k e_k + (1 - p_0)\right) + \sum_{l=0}^\infty p_0^l l (1 - p_0)\\
&=\left(\sum_{k=1}^m p_k e_k + (1 - p_0)\right)\left(\sum_{l=0}^\infty p_0^l\right) + (1 - p_0) \left(\sum_{l=0}^\infty p_0^l l\right)\\
&=\left(\sum_{k=1}^m p_k e_k + (1 - p_0)\right)\frac{1}{1-p_0} + (1 - p_0) \frac{p_0}{(1-p_0)^2}\\
&=\frac{\sum_{k=1}^m p_k e_k}{1-p_0} + \frac{1-p_0}{1-p_0} + \frac{p_0}{1-p_0}\\
&=\frac{1 + \sum_{k=1}^m p_k e_k}{1-p_0}
\end{align}
これで部分問題は解けました。
部分問題が解けたので、部分問題を利用することで、(0, 0)から(n, 9)までの平均遷移数を求められるようになりました。
(n, 9)から(n, 9)までの平均遷移数は0なので、そこから、自分の状態から(n, 9)までの平均遷移数を知っている状態たちを増やしていくことができるのです。
早速先程のプログラムに平均遷移数を求めるメソッドを追加してみます。
module ProbabilisticDFA
class Node
def hop_count_expectation
return @hop_count_expectation_cache unless @hop_count_expectation_cache.nil?
self_loop = @edges.detect {|edge| edge.to == self}
edges_without_self_loop = @edges.reject {|edge| edge == self_loop}
@hop_count_expectation_cache =
(1 + edges_without_self_loop.collect {|edge| edge.probability * edge.to.hop_count_expectation}.inject(0, :+)) /
(1 - self_loop.probability)
end
end
class AcceptStateNode
def hop_count_expectation
0
end
end
end
cost_expectation = gacha_states.fetch([0, 0]).hop_count_expectation * 300
平均金額はcost_expectationで求めることができます。
ここまでお疲れ様でした。
まとめ
ガチャは数学の題材としては楽しいので、みなさんもガチャで遊びましょう(遊び方を間違えている)