この記事は、R Advent Calendar 2016 の23日目の記事です。
2016年も残すところあと8日となり、今年1年を振り返る時期になりました。
本日は、我々がよく使用している R のある関数について振り返ってみたいと思います。
1. はじめに
ちょうどこの Advent Calendar の参加登録が開始した2016年11月後半は、Twitter 上で擬似乱数の生成に関する議論が熱くなっていました。
R ユーザーもシミュレーションをする際など、擬似乱数生成用の関数をよく使用しますよね。
例えば、標準正規分布に従う乱数を生成する場合、以下のようなコードを記述します。
set.seed(123)
x <- rnorm(1e6)
head(x)
# [1] -0.56047565 -0.23017749 1.55870831 0.07050839 0.12928774 1.71506499
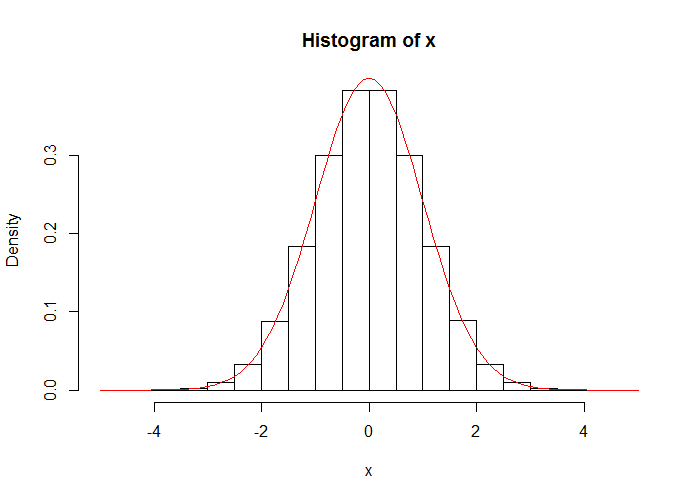
得られた乱数のヒストグラムに標準正規分布の確率密度関数を重ねてあげれば、下図のように様々な値をもつ乱数が理論分布に従う形で、まんべんなくサンプリングされているのが視覚的に確認できます。
hist(x, freq = FALSE)
curve(dnorm, add = TRUE, col = "red")
擬似乱数を生成するためのアルゴリズムや方法はいくつも種類がありますが、R ではどの手法を使って我々が擬似乱数を得ているのか、今一度、おさらいをしてみましょう。
1.1 Rにおける乱数生成用の関数
擬似乱数を得るために R で利用可能な関数には次のようなものがあります。(ここでは、連続型確率分布に従う乱数生成のための関数のみに絞って挙げています。)
本日は、正規乱数に着目をしていきますが、後ほど紹介する既定手法は一般的な方法になりますので、他の連続型確率分布に従う乱数を生成する際にも用いられる方法になります。
| 分布 | 関数 |
|---|---|
| 一様分布 | runif(n, min = 0, max = 1) |
| 正規分布 | rnorm(n, mean = 0, sd = 1) |
| 対数正規分布 | rlnorm(n, meanlog = 0, sdlog = 1) |
| ガンマ分布 | rgamma(n, shape, rate = 1, scale = 1/rate) |
| ベータ分布 | rbeta(n, shape1, shape2) |
| カイ二乗分布 | rchisq(n, df, ncp = 0) |
| t分布 | rt(n, df) |
| F分布 | rf(n, df1, df2) |
| コーシー分布 | rcauchy(n, location = 0, scale = 1) |
| 指数分布 | rexp(n, rate = 1) |
| ロジスティック分布 | rlogis(n, location = 0, scale = 1) |
| ワイブル分布 | rweibull(n, shape, scale = 1) |
1.2 Rにおける乱数種の設定方法
さて、純粋な乱数とは規則性を持たない乱数を言いますが、計算機上で乱数を生成する場合、ある種のアルゴリズムによって発生させるため乱数列は必ず規則性を持ちます。このため、計算機によって得られる乱数を純粋な乱数と区別して、擬似乱数と呼びます。計算機で擬似乱数を生成するメリットは、同じことを繰り返すたびに同じ結果を得ることが出来る、再現性にあります。
Rでは乱数種を set.seed() で設定できます。設定しない場合、現在の時間からシードが作り出されるため、異なるセッションでは異なる結果を得ることになります。
# 乱数種を設定しないと都度異なる結果を与える
rnorm(5)
# [1] -0.8578452 -0.7495221 0.4634515 -0.7394894 -1.1338153
rnorm(5)
# [1] 0.45237627 -0.68540308 0.22306289 0.08193052 -0.41539573
rnorm(5)
# [1] -0.51895154 -0.62834149 0.08808755 0.49019165 -0.05367466
# 乱数種を設定すると、同じ結果が返される
set.seed(123)
rnorm(5)
# [1] -1.1747736 0.6106432 1.1638708 1.3327576 1.1456719
set.seed(123)
rnorm(5)
# [1] -1.1747736 0.6106432 1.1638708 1.3327576 1.1456719
set.seed(123)
rnorm(5)
# [1] -1.1747736 0.6106432 1.1638708 1.3327576 1.1456719
2. 一様擬似乱数生成法
計算機で一様擬似乱数を生成する場合、等確率性を実現するため、$0$(または $1$ )から十分大きい整数 $m$ までのすべての整数値を同じ回数現れるように作ります。得られた系列 {${x_0, x_1, x_2, \ldots }$} について、$u_i = x_i/m$とすれば区間 $[0, 1]$の一様乱数列が得られます。 以下では、R で利用可能な一様擬似乱数生成器と既定手法について整理します。
2.1 Rで指定可能な一様乱数生成器
Rでは、RNGkind() の引数 kind で一様擬似乱数生成用のアルゴリズムを設定することができます。
用法:
RNGkind(kind = NULL, normal.kind = NULL)
引数:
kind: 文字、もしくは NULL。もし kind が文字列ならば、R の RNG を指定した方法に
設定する。もし NULL ならば現在の手法を返す。"default" にすると現在の既定
手法に戻す。
normal.kind: 文字、もしくは NULL。もし kind が文字列ならば、R の正規乱数発生
法を指定した方法に設定する。もし NULL ならば現在の手法を返す。"default"
にすると現在の既定手法に戻す。
用意されたアルゴリズムは下表の通りで、R 1.7.0以降、現在のR 3.2.2 では、"Mersenne-Twister"が既定手法として設定されています。
| アルゴリズム | 周期 | 備考 | |
|---|---|---|---|
| "Wichmann-Hill" | Wichmann-Hill 法 | 6.9536e12 | |
| "Marsaglia-Multicarry" | キャリー付き乗算 | 2^60 以上 | R 1.7.0 以前の既定方法 |
| "Super-Duper" | Super-Duper 法 | 殆どの初期値に対して 約 4.6*10^18 | |
| "Mersenne-Twister" | メルセンヌ・ツイスタ ー | 2^19937-1 | R 1.7.0 以降の既定方法 |
| "Knuth-TAOCP" | Knush(1997) | 2^129 | |
| "Knuth-TAOCP-2002" | 2002年バージョン | 2^129 | |
| "L'Ecuyer-CMRG" | L'Ecuyer, P. (1999) | 2^191 | |
| "user-supplied" | ユーザー提供の発生法を使用 | - |
また、現在の設定値は次のコードで確認することが出来ます。
# 一様乱数生成器および正規乱数生成法の現在の設定値を確認する
RNGkind()
# [1] "Mersenne-Twister" "Inversion"
2.2 既定手法: メルセンヌ・ツイスター(Mersenne Twister)
前節の通り、R 1.7.0 以降、Rでは一様擬似乱数の生成器として メルセンヌ・ツイスターが既定手法に定められています。特に、変更しない場合にはこの方法が用いられますので、ここではメルセンヌ・ツイスターについてもう少し詳しくみてみましょう。
数学的な意味については、メルセンヌ・ツイスターのHP[2] や、開発者である松本先生のスライド[3]等をご参照ください。
(1) 特徴
メルセンヌ・ツイスターの主な特徴には次が挙げられます。
(+) 周期が 2^19937-1 である。
(+) 623次元超立方体の中に均等に分布する。
(-) モンテカルロ法用擬似乱数であり、そのままでは暗号乱数としては使えない。
暗号論的擬似乱数生成器 (CSPRNG) とは、暗号技術での利用に適した特性を持つ擬似乱数生成器 (PRNG) であるが、メルセンヌ・ツイスターは、線形漸化式によって生成されるため予測可能である。従って暗号用途で利用するには同様に、暗号学的ハッシュ関数のような非可逆な操作を通さなければならない。
(2) 従来の既定手法との比較
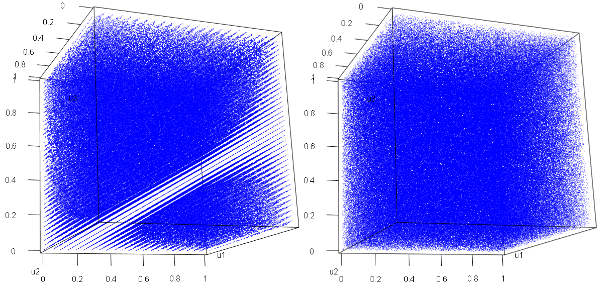
上記のうち、メルセンヌ・ツイスターの特徴(+) を確認するために、他のアルゴリズムの中から、R 1.7.0 以前の既定手法であった、Marsaglia-Multicarry と 現在の既定手法である Mersenne-Twister について、3次元の乱数列を生成した場合の分布を比較してみましょう。
まずは、Marsaglia-Multicarry を用いた場合の乱数の生成とプロットをしてみます。ここで 3次元プロットには {rgl}パッケージの plot3d() を利用しています。
library(rgl)
RNGkind(kind = "Marsaglia-Multicarry")
us_mm <- replicate(n = 1e6, runif(3))
plot3d(t(us_mm), col = "blue", xlab = "u1", ylab = "u2", zlab = "u3", size = 0.0001)
次に、Mersenne-Twisterによる乱数生成とプロットをしてみます。
RNGkind(kind = "Mersenne-Twister")
us_mt <- replicate(n = 1e6, runif(3))
plot3d(t(us_mt), col = "blue", xlab = "u1", ylab = "u2", zlab = "u3", size = 0.0001)
両者を比較すると下図のようになります。左図が Mersagli-Multicaryy 、右図が Mersenne-Twister により得られた乱数列のグラフです。この結果から 2種類の乱数の違いを見て取ることができます。従来の Marsaglia-Multicarry によるものは、構造を持って分布していることがわかります。一方、Mersenne Twisterでは、3次元空間をランダムに満たしており、均等に散らばっていることがわかります。
3. 正規擬似乱数生成法
3.1 Rで利用可能な正規乱数生成法
正規乱数の生成法は RNGkind() の 引数 normal.kind で指定可能で、次のアルゴリズムが用意されています。
現在の R 3.2.2 では、既定手法として "Inversion"、逆関数法が設定されています。
R 1.7.0 以前は、"Kinderman-Ramage" が既定手法でしたが、本アルゴリズムは近似誤差を含むため過去の再現で用いる以外には使用すべきでないとされています。
| アルゴリズム | 備考 | |
|---|---|---|
| "Kinderman-Ramage" | Kinderman & Ramageによる方法 | |
| "Buggy Kinderman-Ramage" | Kinderman-Ramage の擬似乱数発生法のバギー版 | R 1.7.0 以前の既定法 |
| "Ahrens-Dieter" | AhrensおよびDieterのアルゴリズム | |
| "Box-Muller" | Box-Muller 法 | |
| "Inversion" | 逆関数法 | R 1.7.0 以降の既定法 |
| "user-supplied" | ユーザー提供の発生法を使用 |
3.2 既定手法: 逆関数法(Inverse Transform method)
ここでは、現在の既定手法である 逆関数法(Inversion Transform method)について整理します。
逆関数法は、一様乱数をもとに任意の確率分布に従う乱数を生成する方法の一種です。
確率変数 $X$ の分布関数 $F$ が、狭義単調増加関数であり、$ 0 < F(x) < 1$, $ \lim_{x \rightarrow -\infty }F(x) = 0 $, $\lim_{x \rightarrow +\infty } F(x) = 1$ を満たすと仮定します。$ U = F(X) $ とおくと、このとき $F$ に関して、$X$と$U$は一対一に対応するため、逆関数が存在し、$F$の逆関数を$F^{-1}$と書くと、$ X = F^{-1}(U)$と表すことができます。
・ 逆関数法のアルゴリズム
Step 1: 区間 $(0,1)$ の一様乱数 $U$ を生成する
Step 2: $X = F^{-1}(U)$ を計算することにより乱数を得る
(例)
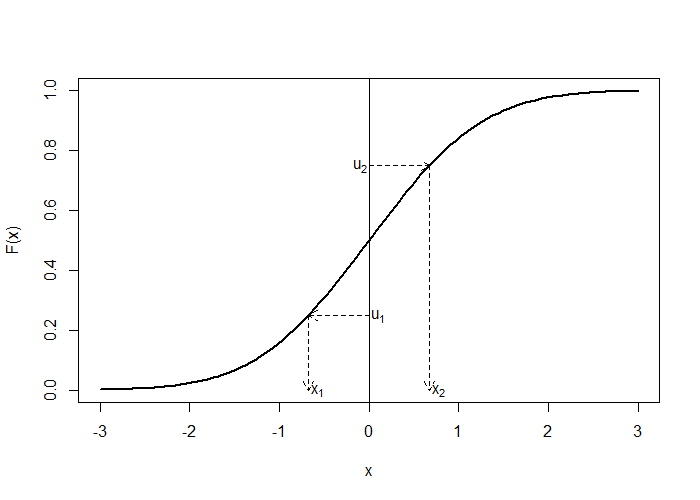
いま、一様乱数 $u_1 = 0.25$, $u_2 = 0.75$ が得られているとします。
標準正規分布の累積分布関数を$F(X)$で表せば、その逆関数$F^{-1}(U)$を用いて、
\begin{eqnarray}
x_1 &=& F^{-1}(u_1) = F^{-1}(0.25) \fallingdotseq -0.67\\
x_2 &=& F^{-1}(u_2) = F^{-1}(0.75) \fallingdotseq 0.67
\end{eqnarray}
を得ることができます。
4. まとめ
本日は、Rにおける正規乱数生成法の既定手法である逆関数法および一様乱数生成時の既定手法であるメルセンヌ・ツイスターについて簡単に整理しました。他のアルゴリズムや、他の確率分布乱数を生成する方法はまたいくつもありますので、興味がある方は [1] などを参考にされてみると良いと思います。
最後に、メルセンヌ・ツイスターの誕生秘話が松本先生のスライド[3]に載っていて面白いので興味が有る方は御覧ください。
というわけで、皆様、良いクリスマスを♡ そして、良いお年を☆
Enjoy R!!!
参考文献
[1] 四辻哲章, 2010, 計算機シミュレーションのための確率分布乱数生成法, プレアデス出版
[2] Mersenne Twister Home Page, http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/mt.html , 最終閲覧日: 2016/12/23
[3] あなたの使っている乱数、大丈夫?, http://www.math.sci.hiroshima-u.ac.jp/~m-mat/TEACH/ichimura-sho-koen.pdf , 最終閲覧日: 2016/12/23