Pythonでベイズ最適化を行うパッケージ GPyOpt

#ベイズ最適化とは
ベイズ最適化は，ガウス過程(Gaussian Process)というベイズ的にカーネル回帰を行う機械学習手法を使って，何らかの関数を最適化する手法です．このベイズ最適化のメリットは様々で，例えば，入力が連続値でない（微分不可能な）関数に適用できたり，局所解がある関数に強かったりします．これらのメリットのため，今後様々な問題に適用可能だと考えられます．ここでは，Pythonでベイズ最適化を行うパッケージであるGPyOptについて使い方を説明します．

#GPyOptのインストール
環境としてanacondaを使います．最新のscipyとGPy(ガウス過程）のパッケージが必要となっています．

$ conda update scipy
$ pip install GPy
$ pip install gpyopt

#入力が1次元の関数最適化（解説）
まずは，入力が1次元の非線形関数を最適化しましょう．
今回は，$f(x)=\cos(1.5x)+0.1x$の関数を，$0\leq x \leq 10$の範囲で最小化することにします．

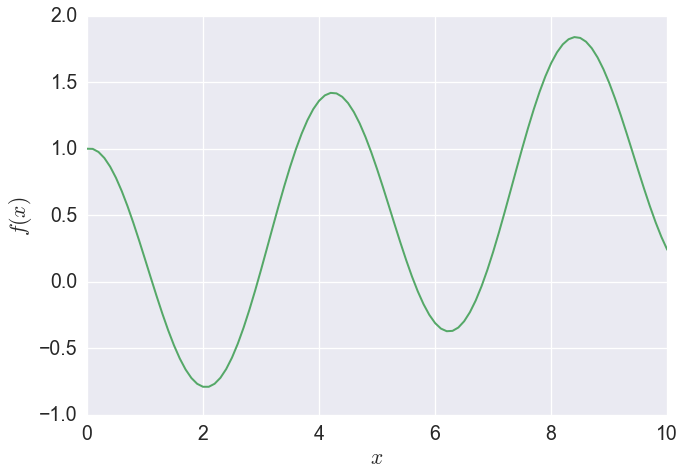
ベイズ最適化ではまず，与えられた範囲でいくつかの入力をランダムにサンプリングします．次に入力したサンプルを関数に通し出力のサンプルも手に入れます．そして，そのサンプルを使って，ガウス過程で回帰を行います．この図では緑が最適化したい関数，青がガウス過程で回帰した関数です．


さて，これから関数が最小になるところを見つけていきます．
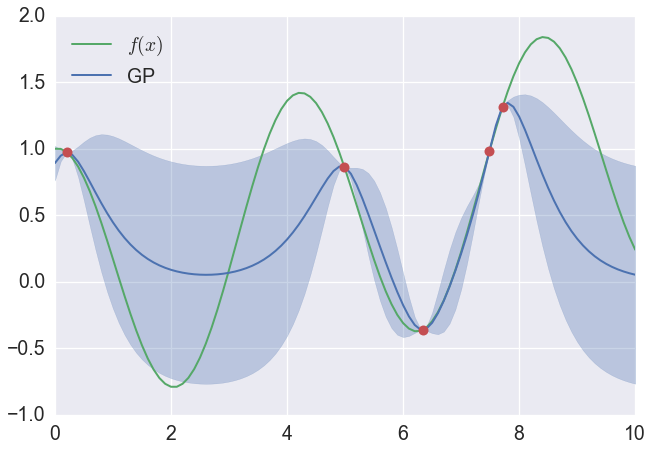
やることは，最小になりそうなxを決めて，そのyを求めるというのを繰り返し行います．どこが最小になりそうなxかということは，色々な基準があるのですが，今回は，この図の青の領域で一番yが小さいところまで及んでいるxを最小になりそうなxとします．この青い領域は，赤い点のデータだけ与えられた場合に，緑の線が入っている可能性の高そうであると考えられる領域です．

さて，この方法で一つサンプリングをしてみます．

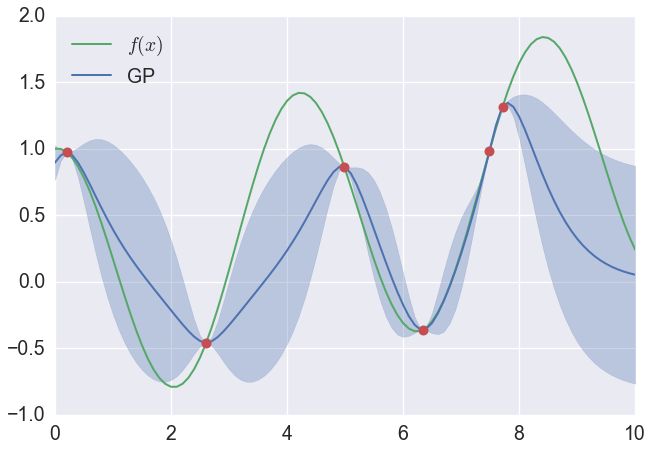
一つサンプリングした後で，大事なことは青い領域が変化していることです．そしてこの状態でまたサンプリング→青い領域の更新→サンプリング→青い領域更新→・・・とすることで，いずれ$f(x)$最小となるxを求めることができるだろうということです．

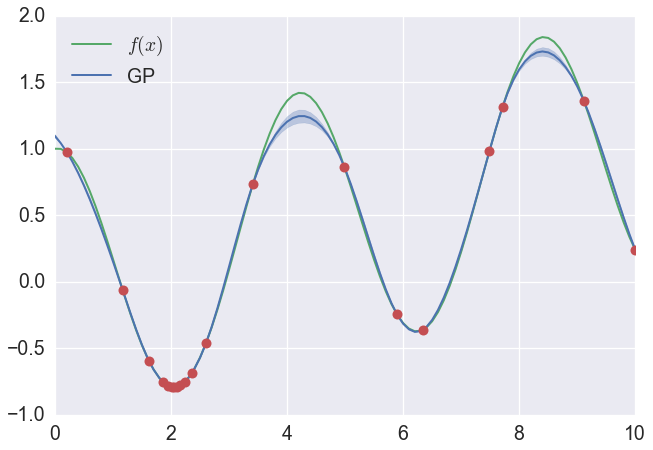
それではいくつかサンプリングした後の図を示します．実際に$x=2$付近でたくさんサンプリングされていて，最終的にはこのサンプリングした中で，実際に$f(x)$が最小になるところを最適解としています．

#入力が1次元の関数最適化（GPyOpt)
それではGPyOptでやってみましょう．

まずはインポートをします．

import GPy
import GPyOpt
import numpy as np 

それから最適化したい関数を定義します．ここではnumpyの関数を指定すれば良いです．

def f(x):
    '''
    今回最適化する非線形関数
    '''
    return np.cos(1.5*x) + 0.1*x

さてここで，xの定義域をまず定義します．'type': 'continuous'は連続であること，'domain': (0,10)は$0\leq x \leq 10$であることを示します．
2行目では，ベイズ最適化用のオブジェクトを取得します．fは最適化したい関数，domainは先ほど定義した定義域，initial_design_numdataは最初に取得するサンプル数を表しています．そして，acquisition_typeは次にサンプリングするxの選び方（'LCB'は先ほどの青い領域が最小になるところを選択するというもの）をさします．

bounds = [{'name': 'x', 'type': 'continuous', 'domain': (0,10)}]
myBopt = GPyOpt.methods.BayesianOptimization(f=f, domain=bounds,initial_design_numdata=5,acquisition_type='LCB')

そして，次のコマンドで繰り返しサンプリングして，最適化します．max_iterはサンプリングする回数を示します．

myBopt.run_optimization(max_iter=15)

最適解を表示します．

print(myBopt.x_opt) #[ 2.05769988]
print(myBopt.fx_opt) #[-0.79271554]

他にも使いそうな関数変数です

myBopt.model.model #ベイズ最適化で使っているガウス過程のモデル(GPyのオブジェクト）
myBopt.model.model.predict #ガウス過程の回帰の関数
myBopt.X,myBopt.Y #サンプリングしたxとy

#入力が2次元の関数最適化
ベイズ最適化は多次元にも適用することができます．ここでは2次元のベイズ最適化を行います．
また，入力変数は離散変数でも良いため，片方の次元は離散変数で行おうと思います．

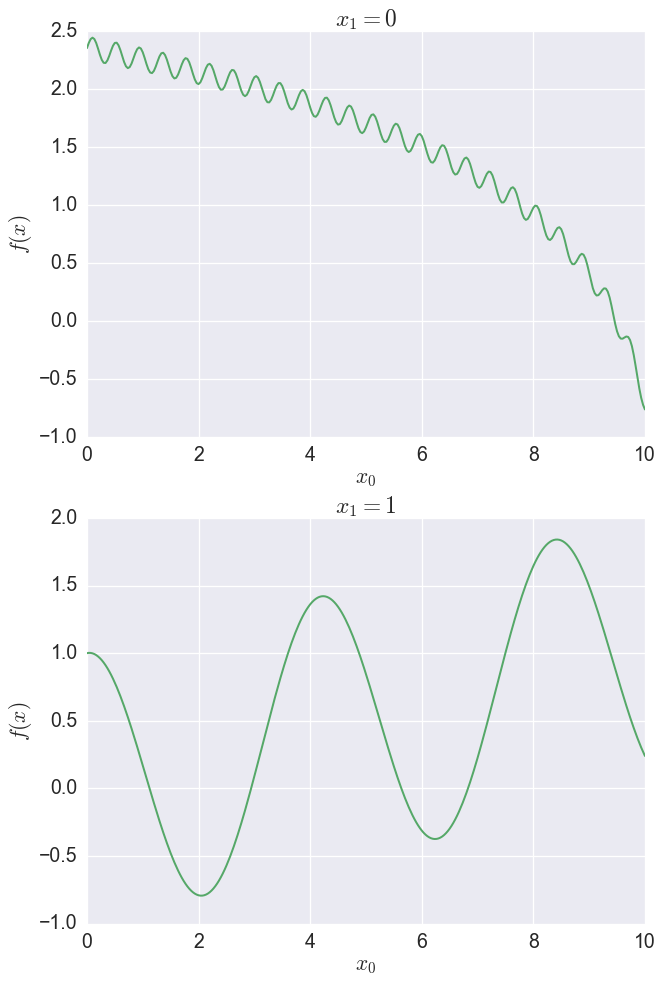
関数は$x_1=0$の場合は$f(x)=\log(10.5-x_0)+0.1\sin(15x_0)$とし，$x_1=1$の場合は$f(x)=\cos(1.5x_0)+0.1x_0$とします．また$0\leq x_1 \leq 10$の範囲で最小化することにします($x_0$は0か1）．

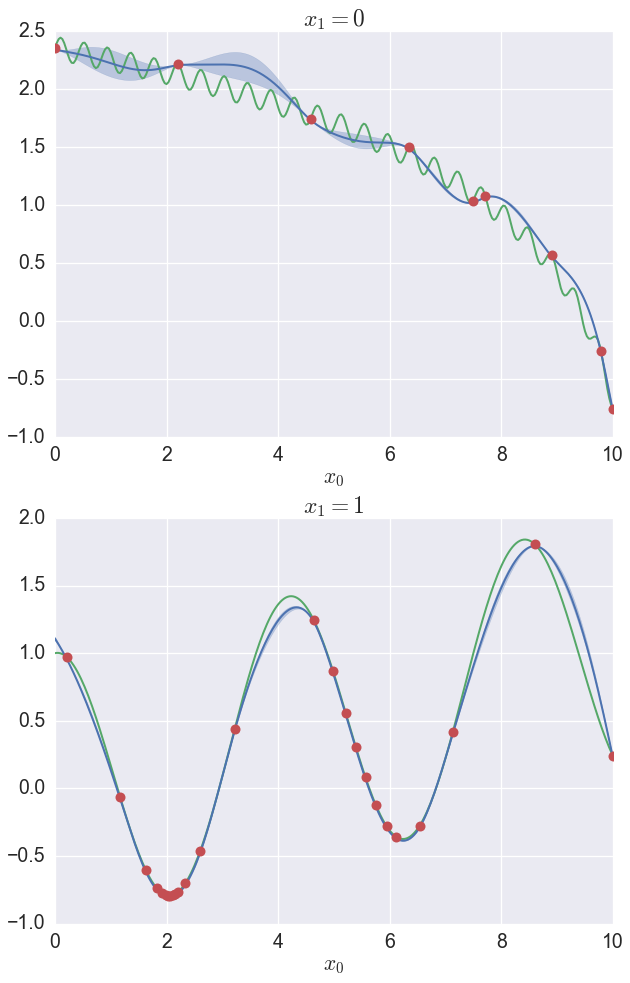
最適化を行うと，次の画像のようになります．

GPyOptでやってみましょう．

import GPy
import GPyOpt
import numpy as np 

def f(x):
    '''
    今回最適化する非線形関数
    '''
    x0,x1 = x[:,0],x[:,1]
    f0 = np.log(10.5-x0) + 0.1*np.sin(15*x0)
    f1 = np.cos(1.5*x0) + 0.1*x0
    return (1-x1)*f0 + x1*f1

bounds = [{'name': 'x0', 'type': 'continuous', 'domain': (0,10)},
          {'name': 'x1', 'type': 'discrete', 'domain': (0,1)}]
myBopt = GPyOpt.methods.BayesianOptimization(f=f, domain=bounds)

myBopt.run_optimization(max_iter=30)

1次元の場合とそんなに変わりませんね．変わったのは，関数に2つの入力も持つようにしたのと，boundsを2つの要素を持つリストにしました．'type': 'discrete'は選択肢を表し，0か1かということを示しています．

最適解を表示します．

print(myBopt.x_opt) #[ 2.0539031  1.       ]
print(myBopt.fx_opt) #[-0.7927657]