概要
DMM配信のブラウザゲーム『艦隊これくしょん -艦これ-』は、擬人化された軍艦(通称:艦娘)を集めて艦隊を編成し、敵である深海棲艦を殲滅するのが主目的のゲームです。
擬人化されたキャラクターは多種多様で、2016/08/20現在で179種類も存在します。それらを収集したり、育成したりするのもこのゲームの楽しみ方の一つです。
さて、彼女達の戦闘は海戦モチーフですので、戦艦などによる砲撃の他に、空母などによる航空戦も存在します。近年では艦載機熟練度などにより空母の重要性が高まっており、上手く行けば**戦艦を超える火力を叩き出すことも珍しくありません。**したがって、『空母にどのような装備を載せるか』は、作戦の可否に関わる重大ポイントだと言えるでしょう。
そこで今回は、空母における装備(艦載機)の最適化を、整数計画問題として立式して解いてみます。
※説明の都合上、軍事用語や艦これ用語が登場します。全部説明すると本筋から脱線してしまいますので端折ります
※以下に出てくる艦これ画像の著作権:(C)2015 DMM.com POWERCHORD STUDIO / C2 / KADOKAWA All Rights Reserved.
戦闘についての概説
艦これにおける戦闘は、主に次の6フェイズに分けられます。
- 索敵フェイズ……索敵により敵艦隊を発見する。成功すると命中・回避率が上昇する
- 航空戦フェイズ……空母の艦載機で敵艦載機を撃墜し、また敵艦隊に爆撃・雷撃を行う
- 開幕雷撃フェイズ……遠距離から、敵艦隊に雷撃を行う
- 砲撃戦フェイズ……射程が長い艦から順に、敵艦隊に砲撃を行う
- 雷撃戦フェイズ……近距離から、敵艦隊に雷撃を行う
- 夜戦フェイズ……夜戦を行う。砲撃戦と比べて、ハイリスクハイリターンなダメージ合戦となる
ここで、空母が関係するのはこのうち航空戦フェイズと砲撃戦フェイズであることに注意してください。
『空母が砲撃?』と疑問に思われる方もいるかもしれませんが、20cm砲を積んだ空母もいますので何もおかしくはない。いいね? アッハイ
また、空母が搭載できる艦載機には、次の3種類が存在します。
- 艦上戦闘機(艦戦)……戦闘機なので艦攻・艦爆に強い。ただし敵艦への攻撃力は皆無
- 艦上攻撃機(艦攻)……敵艦に魚雷を叩き込む。艦これにおいては地上基地への攻撃も可能
- 艦上爆撃機(艦爆)……敵艦に爆弾を落とす。艦これにおいては地上基地へ攻撃できない存在
攻撃だけ考えれば艦攻・艦爆だけを積めばいいのですが、敵艦隊にも空母がいたりしますので、ある程度は艦戦を積む必要があります。制空権の度合いを示した数値を制空値と呼び、この値が大きいほど制空権を握りやすくなります。
したがって、方針としては、『ある程度の制空値を取る』ことと、『その上で最大の火力が出せるようにする』ことが重要です。
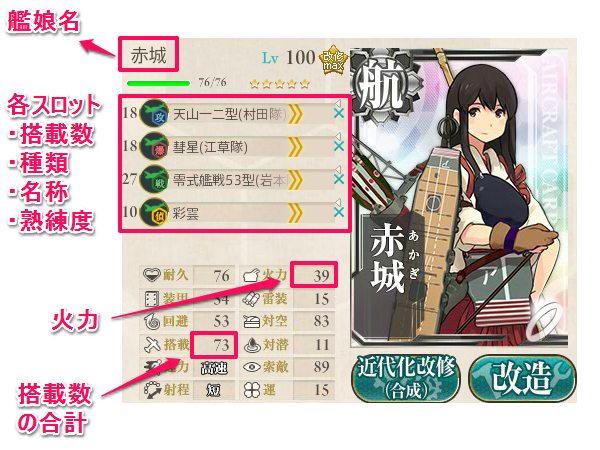
なお、以下の説明では、各艦娘における戦闘用パラメータを知ることが重要になってきます。
下図で一例を示しますので、なるべく覚えてください。
制空値計算について
艦娘の各スロットにはそれぞれ『どの装備を載せるか』を設定できます。
また、各スロットには搭載数が設定されており、数値が大きいスロットほど効果的ということになります。
ここで、『搭載数がNのスロットに、対空の値がPの装備を載せた』とします。その際、そのスロットにおける制空値$C_s=[P\sqrt{N}]$として表されます。これを各スロット毎に計算して合計すれば、最終的な制空値を出すことができます。
この値の目安についてですが、『敵の制空値の1.5倍以上(航空優勢)』か『3倍以上(制空権確保)』のどちらかになるでしょう。
雷撃・爆撃について
航空戦フェイズ
航空戦では、各スロットの艦載機が、ランダムに敵艦を選択して攻撃します。つまり、1隻あたり最大で4隻に同時に攻撃できるわけですね。
1スロットあたりの攻撃力は、搭載数がN・雷装/爆装値がPだとすると$R(25+P\sqrt{N})$として表されます。ここでRは係数で、艦爆だと1.0で固定ですが、艦攻だと0.8と1.5のどちらか(確率は半々)になります。
砲撃戦フェイズ
砲撃戦では、各艦娘が、ランダムに敵艦を選択して攻撃します。航空戦と違い、1隻は同時に1隻しか攻撃できません。
1隻あたりの攻撃力は、空母の素火力をF、雷装値の合計をT、爆装値の合計をBとすると[$55+1.5(F+T+[1.3B])]$として表されます。ただし[]はガウス記号で、『切り捨て』を表します。
備考
厳密に言えば、航空戦には『触接』という攻撃力アップ要素があります。
また、2015年8月10日のアップデートから実装された艦載機熟練度は、制空値増強と攻撃力アップに大きく影響します。
さらに言えば、**『与えられるダメージ=攻撃力-敵の装甲値』**として表されますので、小さな攻撃力が複数<大きな攻撃力が一つということも十分にありえます。
ですが、全部を考慮するとここで説明しきれませんので、とりあえず上記程度の設定で計算を行います。
整数計画モデルによる定式化
条件の整理
まず、目的関数と制約条件を決めます。前者は『最大化 or 最小化させたい数値目標』、後者が『守る必要がある条件』を指します。
- 目的関数……航空戦による攻撃力の和+砲撃戦による攻撃力の和
- 制約条件……『制空値が目標値以上』『1スロットに装備は1つだけ』『各装備数には所持数という制限がある』
大規模な問題になると例にしづらいので、ここは『上記画像の赤城(火力39、搭載数が上から18,18,27,10)一隻に艦載機を載せる』ことを考えます。搭載する艦載機の候補は次の通りです。また、制空値の目標値は90とします。
| 名称 | 種別 | 性能 | 個数 |
|---|---|---|---|
| 零式艦戦21型 | 艦戦 | 対空+5 | 4 |
| 烈風 | 艦戦 | 対空+10 | 1 |
| 流星改 | 艦攻 | 雷装+13 | 2 |
| 彗星 | 艦爆 | 爆装+8 | 3 |
ここで決定変数ですが、間違っても『空母の1つ目のスロットに2番目の装備を積む場合は$slot_1 = 2$、何も積まない場合は$slot_1 = 0$』のようなアホな設定をしないように注意してください。判定がずっと面倒になってしまいますので……。
整数計画法の基本は、0-1決定変数を使い倒すことです。この場合では、『空母の1つ目のスロットに2番目の装備を積む場合は$slot_{1,2}=1$、積まない場合は$slot_{1,2}=0$』とするのが正解となります。つまり、スロットが$X$個・装備が$Y$種類あれば決定変数が$XY$個になるわけですね。
制空値制約
空母のA個目のスロットにB番目の装備を積む場合、A個目のスロットにおける搭載数を$N_A$、B番目の装備における対空値を$P_B$とすると、そのスロットにおける制空値は$C_s=[P_B\sqrt{N_A}]$として表されます。
平方根が出てくると(線形性が崩れるので)ぎょっとしますが、実はこの値$C_s$はAとBが分かれば一定という特徴があります。要するに、事前に計算しておけばタダの整数として扱ってOKです。
つまり、目標制空値を$C_{target}$とすると、制約条件としては$\sum\sum(C_s slot_{A,B})\geq C_{target}$となります。
スロット・所持数制約
当然ですが、1つのスロットに装備は1つしか載りません。
また、所持数より多くのスロットに装備を載せることもできません。
これらの制約も、0-1決定変数なら単純に『合計してその大きさを1 or 所持数と比較』するだけで表現できてしまいます。
もし0-1決定変数でなければ、スロット制約こそ自明なものの、所持数制約は『$slot_a = 2$となる数をカウントして……』といった面倒な処理を書かざるをえなくなることでしょう。
目的関数
航空戦火力は1スロットあたり$R_B(25+P_B\sqrt{N_A})$、砲撃戦火力は全体で$[55+1.5(\sum F+\sum T+[1.3\sum B])]$となります。
前者を$D_a$、後者を$D_g$とすると、目的関数は例えば$D_a+D_b$となることでしょう。ただし、『乱数によって変わる係数』や『整数切り捨て』を考えるのは大変ですので、それぞれ次のように改変します。
- $R_B(25+P_B\sqrt{N_A})\simeq r_B(25+P_B\sqrt{N_A})$ ※$r_B$はB番目の装備が艦攻なら1.15、艦爆なら1.0
- $[55+1.5(\sum F+\sum T+[1.3\sum B])]\simeq 55+1.5\sum F+1.5\sum T+1.95\sum B$ ※整数切り捨てを省いた
最終的な数式
- 『.lp』はLPファイルと呼ばれる、問題記述用の代表的なファイルフォーマット。詳しい書式についてはこちらを参照
- 『定数項は右辺にしか置けない』という初見殺しに注意。目的関数(maximize以下)では右端、制約条件(subject to)では右辺にしか書けない
- 掛け算は『定数 変数』といった形式でしか書けない。これは、『変数×変数』が入ると(広義の)線形計画問題にならないため
- 今回は使用しなかったが、実数の範囲を取りうる変数が混ざっていても(MIPソルバーだと)問題として扱える
maximize \ 目的関数
+ 92 slot_1_3 + 92 slot_2_3 + 106 slot_3_3 + 76 slot_4_3
+ 59 slot_1_4 + 59 slot_2_4 + 67 slot_3_4 + 50 slot_4_4
+ 1.5 sum_f + 1.5 sum_t + 1.95 sum_b + 55
subject to \制約条件
\ 制空値制約
+ 21 slot_1_1 + 42 slot_1_2 + 0 slot_1_3 + 0 slot_1_4
+ 21 slot_2_1 + 42 slot_2_2 + 0 slot_2_3 + 0 slot_2_4
+ 25 slot_3_1 + 51 slot_3_2 + 0 slot_3_3 + 0 slot_3_4
+ 15 slot_4_1 + 31 slot_4_2 + 0 slot_4_3 + 0 slot_4_4 >= 90
\ スロット制約
slot_1_1 + slot_1_2 + slot_1_3 + slot_1_4 <= 1
slot_2_1 + slot_2_2 + slot_2_3 + slot_2_4 <= 1
slot_3_1 + slot_3_2 + slot_3_3 + slot_3_4 <= 1
slot_4_1 + slot_4_2 + slot_4_3 + slot_4_4 <= 1
\ 所持数制約
slot_1_1 + slot_2_1 + slot_3_1 + slot_4_1 <= 4
slot_1_2 + slot_2_2 + slot_3_2 + slot_4_2 <= 1
slot_1_3 + slot_2_3 + slot_3_3 + slot_4_3 <= 2
slot_1_4 + slot_2_4 + slot_3_4 + slot_4_4 <= 3
\目的関数用
sum_f = 39
+ 13 slot_1_3 + 13 slot_2_3 + 13 slot_3_3 + 13 slot_4_3 - sum_t = 0
+ 8 slot_1_4 + 8 slot_2_4 + 8 slot_3_4 + 8 slot_4_4 - sum_b = 0
general \ 整数変数
sum_f sum_t sum_b
binary \ 0-1変数
slot_1_1 slot_1_2 slot_1_3 slot_1_4
slot_2_1 slot_2_2 slot_2_3 slot_2_4
slot_3_1 slot_3_2 slot_3_3 slot_3_4
slot_4_1 slot_4_2 slot_4_3 slot_4_4
end
計算結果
上記サンプルファイル(sample.lp)を、フリーのMIPソルバーであるSCIPで解かせるとこんな感じ。
SCIP> optimize
presolving:
(round 1) 3 del vars, 4 del conss, 0 add conss, 4 chg bounds, 0 chg sides, 0 chg coeffs, 0 upgd conss, 0 impls, 5 clqs
(round 2) 3 del vars, 4 del conss, 0 add conss, 4 chg bounds, 0 chg sides, 0 chg coeffs, 4 upgd conss, 0 impls, 5 clqs
(round 3) 3 del vars, 4 del conss, 0 add conss, 4 chg bounds, 1 chg sides, 1 chg coeffs, 8 upgd conss, 0 impls, 6 clqs
(0.0s) probing cycle finished: starting next cycle
(round 4) 12 del vars, 4 del conss, 0 add conss, 4 chg bounds, 1 chg sides, 1 chg coeffs, 8 upgd conss, 0 impls, 14 clqs
(round 5) 14 del vars, 9 del conss, 0 add conss, 4 chg bounds, 1 chg sides, 9 chg coeffs, 8 upgd conss, 0 impls, 10 clqs
(0.0s) probing cycle finished: starting next cycle
presolving (6 rounds):
14 deleted vars, 9 deleted constraints, 0 added constraints, 4 tightened bounds, 0 added holes, 1 changed sides, 9 changed coefficients
0 implications, 10 cliques
presolved problem has 5 variables (5 bin, 0 int, 0 impl, 0 cont) and 3 constraints
1 constraints of type <knapsack>
2 constraints of type <setppc>
transformed objective value is always integral (scale: 95.5)
Presolving Time: 0.00
time | node | left |LP iter|LP it/n| mem |mdpt |frac |vars |cons |cols |rows |cuts |confs|strbr| dualbound | primalbound | gap
T 0.0s| 1 | 0 | 0 | - | 182k| 0 | - | 5 | 3 | 5 | 3 | 0 | 0 | 0 | -- |5.850000e+001 | Inf
* 0.0s| 1 | 0 | 0 | - | 180k| 0 | - | 5 | 0 | 5 | 3 | 0 | 0 | 0 |1.540000e+002 |1.540000e+002 | 0.00%
0.0s| 1 | 0 | 0 | - | 180k| 0 | - | 5 | 0 | 5 | 3 | 0 | 0 | 0 |1.540000e+002 |1.540000e+002 | 0.00%
SCIP Status : problem is solved [optimal solution found]
Solving Time (sec) : 0.00
Solving Nodes : 1
Primal Bound : +1.54000000000000e+002 (2 solutions)
Dual Bound : +1.54000000000000e+002
Gap : 0.00 %
SCIP> display solution
objective value: 154
slot_1_1 1 (obj:0)
slot_2_1 1 (obj:0)
slot_3_2 1 (obj:0)
slot_4_3 1 (obj:76)
sum_t 13 (obj:1.5)
sum_f 39 (obj:1.5)
要するに、『目的関数の最大値は154であり、(問題の対称性のせいで)それになる組み合わせは2つ存在する』ことと、
『1・2スロット目に零式艦戦21型、3スロット目に烈風、4スロット目に流星改を置くのが最善』ということです。
また、目標制空値を60に書き換えると、目的関数の最大値は281.5に上昇し、装備も『流星改・流星改・烈風・零式艦戦21型』に変化します。
手作業だと面倒な試行錯誤が、ソルバーを使えば即座に求まるというわけですね。
まとめ
今回は艦これを題材に、整数計画問題をMIPソルバーで解いてみました。
また、上記内容を更に発展させて実用化したソフトウェアをWeb上で公開してます。よろしければ是非使ってみてください。