この記事は物理数学の直観的方法の4章の自分なりの平凡なまとめを淡々と描くものです。過度な期待はしないでください。
オイラーの公式は以下の式ですね。
e^{i\theta}=\cos\theta+i\sin\theta
右辺の方は簡単です。
三角関数の定義より、
f(\theta)=\cos\theta+i\sin\theta
は、横軸がcosθ、縦軸がisinθですねなので、
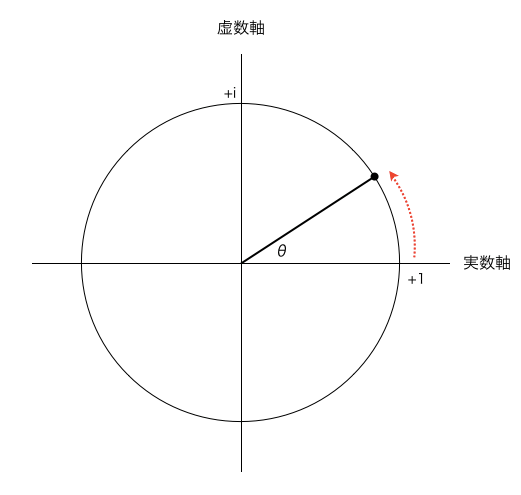
以下のようにガウス平面上を円運動します
右辺の方がわかったので、
一緒に左辺も見てみましょう
f(\theta)=e^{i\theta}
こちらは、よくわからないので、一旦微分してみます
合成関数の微分を考えるのが楽です
分離します
f(\theta)=e^u\\
u = i\cdot \theta
それぞれ微分します
上部=e^u\\
下部=i
合成します
f'(\theta)=e^{i\theta} \cdot i
微分できました。
すると、新しいことがわかります。
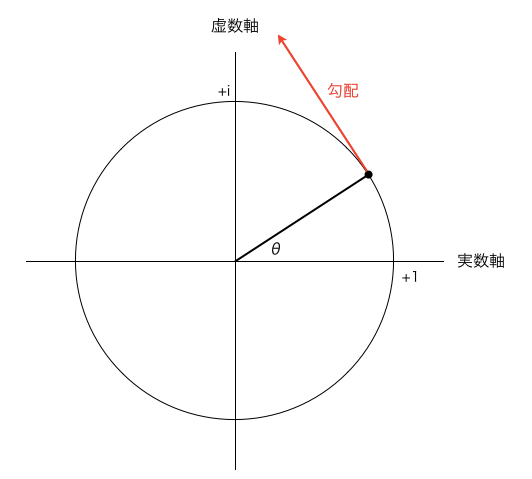
「ある地点f(θ)の値、に虚数単位iを掛けた値がその時点での勾配である」
ということです。
iを掛けるというのは、ガウス平面上で90度回転することですから、
イメージは以下のようになります。
f(\theta)=e^{i\theta}
は、スタート地点については、θに0を入れてみると+1で、
またすべての位置に対して常にこれが言えるわけですので、
やはり、以下のようにガウス平面上を円運動するのです
オイラーの公式はこれを示していたのですね
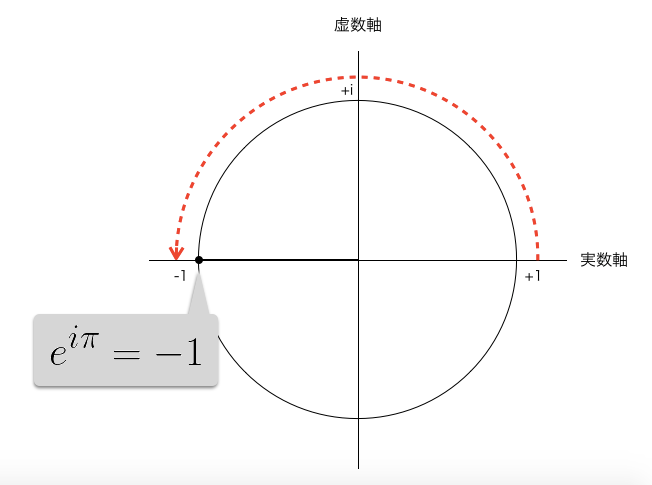
そして数学の至宝とも言われているオイラーの等式
e^{i\pi} = -1
そうそれはスタート地点から一度虚数の海に飛び出していき、
ちょうど π分進む長い航海のあと、
再び実数軸に帰ってきたその瞬間のことを述べていたのです
これはもはや自明のことのように感じるのではないでしょうか