コクのある乱数
もはや何周遅れかわかりませんが、
元ネタは深津さんの以下のツイートです。
アニメーションの監修で、「 Random();の代わりに、(Random()+Random()+Rrandom()+Random()+Random())/5.0f; を使うと、動きにコクが出る」と言ったら、ピュアオーディオ扱いされるのですが・・・これは根拠のあるアルゴです。
— 深津 貴之 (@fladdict) 2016年11月3日
実際のところ、任意の分布をもつ確率変数の無限和というのは正規分布に近づくというのはわかっています。
これはKOMIYAさんの記事でも解説されております。
[「一様乱数の平均値を正規乱数として代用する」という話をゆるふわ統計的に検証する]
(http://k11i.biz/blog/2016/11/05/approximate-gaussian-rng/)
ただこの記事にもありますが、コクの話は、
「一様乱数でもなく正規乱数でもなく、でもちょっと正規分布に従っているっぽい乱数」
がよりそれっぽい動きやビジュアルをプログラミングする場合にはよく役に立つ、という主張になります。
分布の組み合わせ
本題に入る前に、確率の組み合わせについてすこしおさらいします。
経済数学の直観的方法 確率・統計編に大変わかりやすい例がありましたので、そちらを紹介します。
コインを投げて、裏が出たら-aポイント、表が出たら+aポイント手に入り、それを何回か繰り返し合計点を競うゲームを考えます。ここでその結果をAします。
やや唐突ですが、ここでAの絶対値|A|を考えます。
例えば2回の場合、
|A| = |a_1 + a_2|
絶対値ですから、2乗してルートをとっても良いはずです。
|A| = \sqrt { (a_1 + a_2)^2 } \\
|A| = \sqrt { a_1^2 + a_2^2 + 2 a_1 a_2 }
今度は3回の場合はどうでしょうか?
|A| = \sqrt { (a_1 + a_2 + a_3)^2 } \\
|A| = \sqrt { a_1^2 + a_2^2 + a_3^2 + 2(a_1 a_2 + a_2 a_3 + a_3 a_1) }
さらに4回の場合はどうでしょうか?
|A| = \sqrt { (a_1 + a_2 + a_3 + a_4)^2 } \\
|A| = \sqrt { a_1^2 + a_2^2 + a_3^2 + a_4^2 + 2(a_1 a_2 + a_3 a_1 + a_4 a_1 + a_2 a_3 + a_2 a_4 + a_3 a_4) }
さて、だんだんきつくなってきましたが、この式の中でも前半の2乗の和の部分と、後半の2つのaの積でできている部分の2つに大きく別れました。ただ、この後半部分、前提としてコイン投げで+か-が等しい確率で発生しますので、|A|をたくさん繰り返したとき、この部分の成分は0に近づいていくことがわかります。
つまるところ、|A|で大事な部分は前半の2乗の和の部分であるといえます。
コイン投げで+か-が等しい確率で発生するため、aをまとめることができます。
すると、
|A| = \sqrt { a_1^2 + a_2^2 + a_3^2 + a_4^2 } \\
|A| = \sqrt { 4 a^2 }
|A|は上の値に近づいていくとわかります。
ここで一回やったときの絶対値が、
|A| = \sqrt { a_1^2 } = a
に収束し、N回やった絶対値は
|A| = \sqrt { a_1^2 + a_2^2 + a_3^2 ... } = \sqrt { N a_1^2 } = a\sqrt {N}
と収束するため、コインをN回繰り返すと、ルートN倍に|A|が広がっていくことを意味します。
また同時に|A|が広がるということは、全体的な値も同じスケールで広がることを意味し、
標準偏差についても同じスケールで広がっていくことがイメージできます。
\sigma = \sqrt { \sigma_1^2 + \sigma_2^2 + \sigma_3^2 ... } = \sqrt { N \sigma_1^2 } = \sigma\sqrt {N}
また、
|A_1|^2 = a_1^2 = a^2 \\
|A_2|^2 = a_1^2 + a_2^2 + a_3^2 ... = N a^2
のように2乗の場合は、単に和で広がっていくこともまた同様にわかります。
ここから分散についてもこの規則に支配されていると言えます。
\sigma_a^2 = \sigma_1^2 = \sigma^2 \\
\sigma_b^2 = \sigma_1^2 + \sigma_2^2 + \sigma_3^2 ... = N \sigma^2
正規化
話は戻って、コクを出すアルゴリズム、少し使いづらい点がいくつかあります。
まずは一様乱数の個数によって、組み合わせたあとの乱数の標準偏差が違ってきてしまう点です。
これは結局、先程の議論と同じことが原因で、N回繰り返すと標準偏差が ルートN 倍になってしまうためです。
ですが上記のアイディアに基づいて、生成される乱数に、標準偏差が一定になるように正規化係数を掛けて調整することは可能なはずです。
なのでまずは元になる一様乱数の分散について考えてみます。
ここで今回考える一様乱数は、0~1より、-1~1の乱数を考えます。平均が0になったほうが使い勝手的にも計算的にも楽なんじゃないかというところです。
-1~1一様乱数で生成される数をx1, x2, x3...とすると、分散は以下の式になります
\sigma ^{ 2 }=\frac { 1 }{ N } \sum _{ i=1 }^{ N } x_{ n }^{ 2 }
これがいくつになるかを考えます。
\sigma ^{ 2 }=\frac { 1 }{ N } \sum _{ i=1 }^{ N } x_{ n }^{ 2 }\\ =\frac { 2 }{ N } \frac { 1 }{ 2 } \sum _{ i=1 }^{ N } x_{ n }^{ 2 }\\ =\frac { 1 }{ 2 } \sum _{ i=1 }^{ N } x_{ n }^{ 2 }\frac { 2 }{ N }
ここでNで極限を取ると、おっと、これはリーマン積分でした
\sigma ^{ 2 }=\lim _{ N\to \infty } \frac { 1 }{ 2 } \sum _{ i=1 }^{ N } x_{ n }^{ 2 }\frac { 2 }{ N } \\ =\frac { 1 }{ 2 } \int _{ -1 }^{ 1 }{ { x }^{ 2 } } dx\\ =\frac { 1 }{ 2 } [\frac { 1 }{ 3 } { x }^{ 3 }]^{ -1 }_{ 1 }\\ =\frac { 1 }{ 2 } (\frac { 1 }{ 3 } +\frac { 1 }{ 3 } )=\frac { 1 }{ 3 }
分散は1/3で、標準偏差はそのルートになります。
これは実際に乱数を発生させて確かめることもできます。
結局複数の確率変数を足し合わせてできた新しい変数の分散はそれぞれの分散の和になるわけなので、
\sigma^2 = \frac{1}{3}N
と分散,標準偏差がわかりました。
あとは足し合わせてできた数を標準偏差で除算すれば、すべて-1~+1に正規化されることになります。
C++で表現すれば、
// 正規化されたコクのある乱数
double koku(int n) {
n = std::max(1, n);
double s = 0.0;
for (int i = 0; i < n; ++i) {
s += random_xor.uniform(-1.0, 1.0);
}
double sigma2 = n / 3.0;
return s / sqrt(sigma2);
}
となります。
だいぶ使い勝手がよくなりました。
連続化
さて、もうひとつ使いにくいポイントとして、Nが整数であるという点があります。
せっかくNによって正規分布具合をコントロールできるのですから、どうせなら小数点でパラメータを調整できたほうがいくぶん便利な気がします。
そこで、整数部分は今まで通り計算して、少数部分は最後の1回ということで別途計算することにします。別途計算したとしても、結局分散を足せばいいわけですから簡単です。
やり方は何個かありそうですが、ここでは小数部分をa(0.0~1.0)として、最後の一様乱数の幅が(-a~a)になるようにしてみます。
ここで最後の部分、-a~aの一様乱数の分散を一応計算しておきましょう。
\sigma ^{ 2 }=\frac { 1 }{ N } \sum _{ i=1 }^{ N } x_{ n }^{ 2 }\\ =\frac { 1 }{ 2a } \frac { 2a }{ N } \sum _{ i=1 }^{ N } x_{ n }^{ 2 }\\ =\lim _{ N\to \infty } \frac { 1 }{ 2a } \sum _{ i=1 }^{ N } x_{ n }^{ 2 }\frac { 2a }{ N } \\ =\frac { 1 }{ 2a } \int _{ -a }^{ a }{ { x }^{ 2 } } dx\\ =\frac { 1 }{ 2a } [\frac { 1 }{ 3 } { x }^{ 3 }]^{ -a }_{ a }\\ =\frac { 1 }{ 2a } (\frac { 1 }{ 3 } { a }^{ 3 }+\frac { 1 }{ 3 } { a }^{ 3 })=\frac { 1 }{ 3 } { a }^{ 2 }
これで最後の部分の分散がわかりました。これを踏まえてC++に落とし込むと、
// 正規化し、連続化されたコクの有る乱数
double koku(double nf) {
nf = std::max(1.0, nf);
int n = std::floor(nf);
double a = nf - n;
double s = 0.0;
for (int i = 0; i < n; ++i) {
s += random_xor.uniform(-1.0, 1.0);
}
s += random_xor.uniform(-1.0, 1.0) * a;
double sigma2 = n / 3.0 + a * a / 3.0;
return s / std::sqrt(sigma2);
}
というようになります。
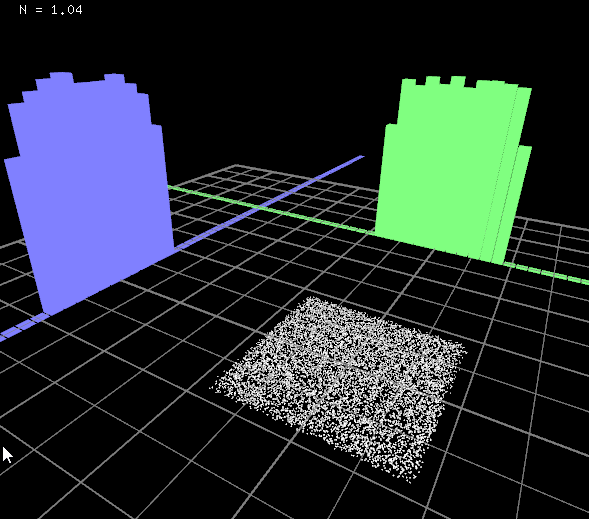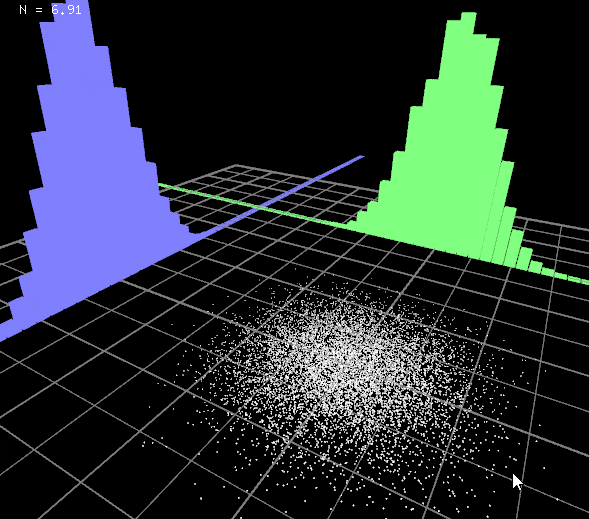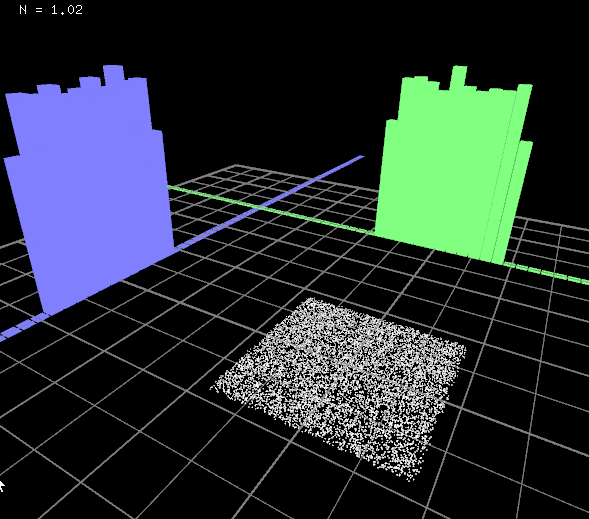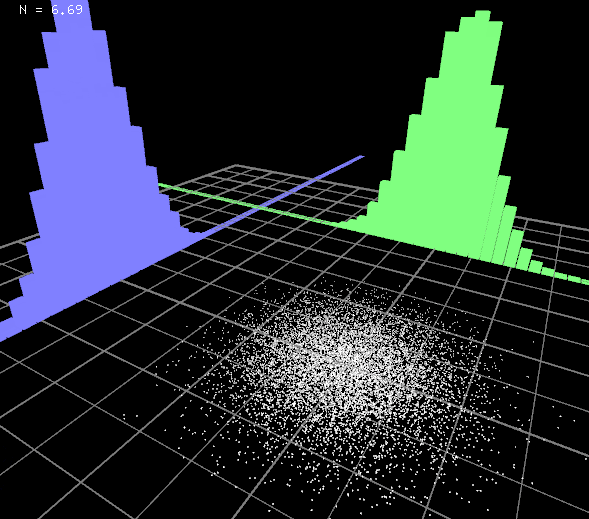
ビジュアライズ
お疲れ様でした。これでだいぶ使い勝手の良いコクの有る乱数ができました。
簡単にビジュアライズしてみましょう。
とてもシームレスにパラメータを調整できるようになりました。
簡単なアルゴリズムに、深いロジックが見え隠れする大変おもしろいトピックでした。