お札と小銭の分布
もし、必ず財布の重量が最小になるように支払っていたら、財布の中身はどのような分布になるでしょうか?
シミュレーション
シミュレーションで確かめてみましょう。
- 1万円は無限にあるものとします。
- 1万回、商品を買って分布をみます。(最初の100回は無視します)
- 商品の金額は、100円~9999円とし、ベンフォードの法則に従う分布とします。
- 乱数の発生(rand_from_prob)は、Walker's Alias Methodを用います。
- 支払い後に重量を最小化するのは、組合せ最適化で計算します。
Pythonで計算
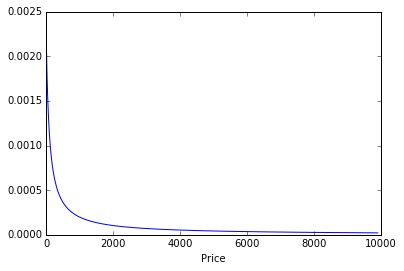
まずは、ベンフォードの法則で100円~9999円の重み(wgt)を作ってみましょう。
python
import numpy as np, matplotlib.pyplot as plt
from math import log
# ベンフォードの法則
wgt = np.array([log((i+1)/i, 10000) for i in range(100, 10000)])
wgt /= sum(wgt)
plt.plot(wgt)
plt.xlabel('Price')
重量を最小化した後の個数を返すchangeを定義します。
python
from pulp import *
money_val = (1, 5, 10, 50, 100, 500, 1000, 5000)
money_wgt = (1.0, 3.7, 4.5, 4.0, 4.8, 7.0, 1.0, 1.0)
def change(price):
m = LpProblem() # 数理モデル
x = [LpVariable('x%d'%i, lowBound=0, cat=LpInteger)
for i in range(len(money_val))] # 支払い後の個数
m += lpDot(money_wgt, x) #目的関数(支払い後の重量)
m += lpDot(money_val, x) == price # 支払い後の金額
m.solve()
return [int(value(i)) for i in x]
シミュレーションしてみましょう。試しに1000円札の分布をみてみます。
python
price = 0 # 現在の所持金
warm, nrun = 100, 10000
res = []
for i, p in enumerate(rand_from_prob(wgt, warm+nrun)):
price -= p
if price < 0:
price += 10000
if price:
res.append(change(price))
a = np.array(res[-nrun:])
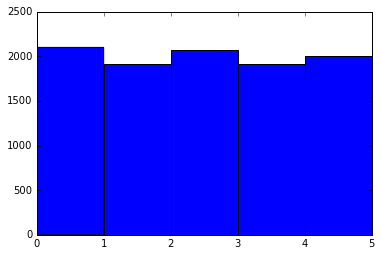
plt.hist(a[:,6], bins=5, range=(0, 5)) # 1000円札の分布
等確率ですね。他の硬貨や5000円札も同様でした。
結論
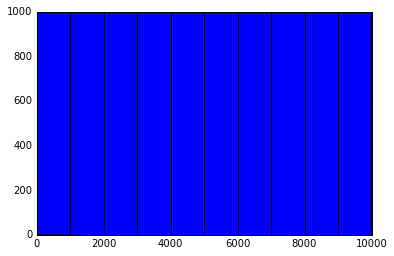
等確率になるようです。総額の分布も0円から9999円の等確率になります。
python
import pandas as pd
from itertools import product
r2, r5 = range(2), range(5)
ptn = [np.dot(money_val, n) for nn in
product(r5, r2, r5, r2, r5, r2, r5, r2)]
plt.hist(ptn)
print(pd.DataFrame(ptn).describe())
>>>
0
count 10000.00000
mean 4999.50000
std 2886.89568
min 0.00000
25% 2499.75000
50% 4999.50000
75% 7499.25000
max 9999.00000
以上