はじめに
BUGS (Beyesian inference using Gibbs Sampling) のWebサイトにある例題のうち,今回"Beetle"をPythonで解いてみる. ”Beetle"の概要だが,Carbon Disulphide(二硫化炭素)環境下にカブトムシを入れ,ガスの濃度に応じてカブトムシの死亡率(5時間後に何匹死んだか)についてデータ分析するというものである.与えられるのはカウントデータなので,二項分布で離散的な統計モデルを構成する問題となる.
ツールとしては,まず初めにstatsmodelsを用いて分析(GLMの計算)を行い,次にPyMC3で計算を行った.
与えられているBliss(1935)のデータセットを参照する.
Table. Bliss's data
| Concentration(xi) | Num. of beetles(ni) | Num. of killed (ri) |
|---|---|---|
| 1.6907 | 59 | 6 |
| 1.7242 | 60 | 13 |
| 1.7552 | 62 | 18 |
| 1.7842 | 56 | 28 |
| 1.8113 | 63 | 52 |
| 1.8369 | 59 | 52 |
| 1.8610 | 62 | 61 |
| 1.8838 | 60 | 60 |
これと一緒に掲載されていたBUGS scriptは,以下の通りである.
model
{
for( i in 1 : N ) {
r[i] ~ dbin(p[i],n[i])
logit(p[i]) <- alpha.star + beta * (x[i] - mean(x[]))
rhat[i] <- n[i] * p[i]
culmative.r[i] <- culmative(r[i], r[i])
}
alpha <- alpha.star - beta * mean(x[])
beta ~ dnorm(0.0,0.001)
alpha.star ~ dnorm(0.0,0.001)
}
やってしまいがちな「ダメ」方法
今回のようなロジスティック回帰の問題では,求めたいモデルが縦軸を 0<p<1 とした確率の関数であるのに対し,与えられるのが「総個体数」と「死亡数」というカウントデータである.よくやってしまうのが,最初にデータの前加工として比率を算出し,それにfitするモデルを求めるというやり方である.これをcodeにすると以下のようになる.
n_betl = np.array([59, 60, 62, 56, 63, 59, 62, 60])
y_betl = np.array([6, 13, 18, 28, 52, 53, 61, 60])
y1 = y_betl *1.0 / n_betl # calculated the proportion of y : n
x1 = np.array([1.6907, 1.7242, 1.7552, 1.7842,
1.8113, 1.8369, 1.8610, 1.8839])
x1a = sm.add_constant(x1)
model_g1 = sm.GLM(y1, x1a, family=sm.families.Binomial(sm.families.links.logit))
res1 = model_g1.fit()
print res1.summary()
このようなcodeを書いて出来たと思っていたが,「データ解析のための統計モデリング入門」を開くと久保先生に怒られてしまうことが分かる.
「割り算値(観測データ/観測データ)による回帰や相関分析は現在でも見かける方法です.(中略)このように変形した観測地を統計モデルの応答関数にするのは,不必要であるばかりでなく,場合によっては間違った結果を導きかねないものです.」
(ごもっとです.この本からはいつもお叱り,注意をいただいています.)
割り算値によらない,カウントデータをモデル化する手法として以下の2つが考えられる.
- Binomial distrubutionとパラメータをきちんと引数としてGLM(=Generalized Linear Model) functionに渡して回帰計算を行う.
- 集計されているデータを,一つ一つが(Beetleが死亡していない or 死亡を示す)ラベルを持つデータに伸長し,そのデータを回帰分析にかける.
明らかに,前者のやり方がスマートである.因みに"R"のcodeは次の通りである.
# R's model expression
beetle.glm <- glm(cbind(y, n-y) ~ dose(=x1), family=binomial(link=logit))
R codeで使っている "cbind(y,n-y) ~ dose" のような式表記をうまくPython用に置き換えることができなかった.statsmodels.formula で前記のような統計モデル式を取り扱うことは可能のようだが,情報不足で「組み合わせ」(combination... nCy)を表現する(statsmodels.formula用の)式を作成できず.(質問サイトなどいろいろ調べましたが,結局断念となりました..)仕方がないので,後者のやり方をとることにした.
statsmodelsによるLogistic Regression
書き直したcodeは,以下の通りである.
import statsmodels.api as sm
import statsmodels.formula.api as smf
# prep data arrays by expanding tabulated data
resp_expand = np.array([])
x1_expand = np.array([])
for i in range(len(n_betl)):
ni = n_betl[i] ; yi = y_betl[i]
resp_expand = np.append(resp_expand, np.repeat(0, (ni-yi)))
resp_expand = np.append(resp_expand, np.repeat(1, yi))
x1_expand = np.append(x1_expand, np.repeat(x1[i], ni))
mydf = pd.DataFrame()
mydf['x1_ex'] = x1_expand
mydf['resp'] = resp_expand
myformula = 'resp ~ x1_ex'
model_g1 = smf.logit(myformula, data=mydf)
# model_g1 = smf.glm(myformula, data=mydf, family=sm.families.Binomial()) これでもOK.
result1 = model_g1.fit()
print result1.summary()
下から4行めの通り logit() を使い,うまく計算できた.summary() を示す.
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: resp No. Observations: 481
Model: GLM Df Residuals: 479
Model Family: Binomial Df Model: 1
Link Function: logit Scale: 1.0
Method: IRLS Log-Likelihood: -186.24
Date: Tue, 25 Aug 2015 Deviance: 372.47
Time: 09:46:41 Pearson chi2: 436.
No. Iterations: 8
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -60.7175 5.181 -11.720 0.000 -70.871 -50.563
x1_ex 34.2703 2.912 11.768 0.000 28.563 39.978
==============================================================================
PyMC3 によるLogistic Regression
PyMC3ではベイズ推定の作法に従い,事前分布(prior distribution)と尤度関数(likelihood)を与えてモデル化し,それをMCMC (Marcov chain Monte Carlo)で解くというやり方になるが,ここでは上述のような「割り算値を使ってしまう」こともなく,自然にBinomial distributionを記述してモデル化できてしまう.
(参照したPyMC Tutorial コードがきちんとできているおかげとも言えますが...)
以下のようなcodeを用意し,シミュレーションを実行した.
import pymc3 as pm
n_betl = np.array([59, 60, 62, 56, 63, 59, 62, 60])
y_betl = np.array([6, 13, 18, 28, 52, 53, 61, 60])
x1 = np.array([1.6907, 1.7242, 1.7552, 1.7842,
1.8113, 1.8369, 1.8610, 1.8839])
mymodel1 = pm.Model()
def invlogit(x):
return pm.exp(x) / (1 + pm.exp(x))
with mymodel1: # model definition
mytheta = pm.Normal('theta', mu=0, sd=32, shape=2) # 2-dim array
p = invlogit(mytheta[0] + mytheta[1] * x1)
y_obs = pm.Binomial('y_obs', n=n_betl, p=p, observed=y_betl)
with mymodel1: # running simulation
start = pm.find_MAP()
step = pm.NUTS()
trace1 = pm.sample(10000, step, start=start)
pm.summary(trace1)
pm.traceplot(trace1)
traceplot()は,以下の通り.(初稿にあったsummary()は削除しました.)
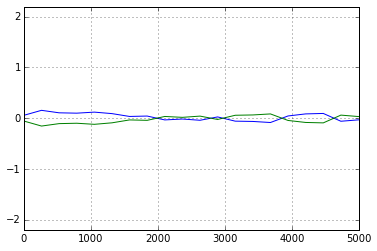
Fig. Traceplot (Logistic Regression)

今回,機械的に10000 step と設定してMCMC計算を行ったが,一応,Geweke法収束を確認する.(因みに計算時間は,どのMCMC計算も 30秒前後でした.)
収束に関し,問題なし.
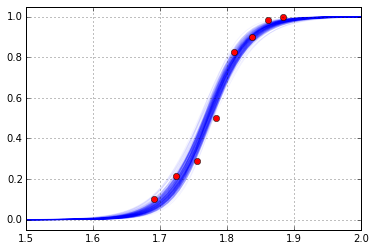
Trace結果を用いて作図したFitting Plotは以下.
計算結果比較
(追記:初稿では,probitモデル,c-loglogモデルの説明を記載していましたが,記事が冗長でしたので省略することにしました.)
Table 計算結果の比較
| Method | Link func. | theta1 (mean) | theta1 (SD) | theta2 (mean) | theta2 (SD) |
|---|---|---|---|---|---|
| BUGS (reference) | logit | -60.79 | 5.147 | 34.31 | 2.893 |
| BUGS (reference) | probit | -35.04 | 2.646 | 19.79 | 1.488 |
| BUGS (reference) | c-loglog | -39.77 | 3.211 | 22.15 | 1.788 |
| GLM, statsmodels | logit | -60.71 | - | 34.27 | - |
| MCMC, PyMC3 | logit | -59.56 | 4.911 | 33.62 | 2.761 |
3者間で(BUGS(logit) vs. statsmodels vs. PyMC3)で概略,整合性がとれているように見える.(今回は,PyMC3よりstatsmodelsの方でだいぶ苦労されられました.)
参考文献 (web site)
- OpenBUGS Examples
http://www.openbugs.net/Examples/Beetles.html - Stan Examples
https://github.com/stan-dev/example-models/wiki - statsmodels document
http://statsmodels.sourceforge.net/documentation.html - PyMC3 tutorial
https://pymc-devs.github.io/pymc3/getting_started/ - データ解析のための統計モデリング入門 (岩波書店)
https://www.iwanami.co.jp/cgi-bin/isearch?isbn=ISBN978-4-00-006973-1 - 実践R統計分析(オーム社)
http://shop.ohmsha.co.jp/shop/shopdetail.html?brandcode=000000004304&search=R+%C5%FD%B7%D7&sort=