※深層学習の調査のなかで、気になった論文を共有していきます。
原文タイトル
特徴抽出時の(自己符号化器の)明示的不変性(Contractive Auto-Encoders_Explicit Invariance During Feature Extraction)
Salah Rifai (2011)
1. 要約
- 事前学習として、多くの教師なし学習手法が生み出されている中、著者は新しいタイプの自己符号化器を考案した。
- 名称は、縮小自己符号化器(CAE)
- 過学習を防ぐために、重みベクトルの更新に、あるペナルティ項を加える。これ自体は、過去の自己符号化器にも見られた(スパース正則化や重み減衰など)。
- 加える項目に、革新性がある。ヤコビアンをフロベニウス正規化した項を加える。詳細は、2.の理論の項に譲る。
2. 骨子の理論
はじめに、加えるべきペナルティ項を記載する;
$$||J_f(x)||^2_F = \sum_{ij}(\frac{\partial h_j(x)}{\partial x_i})^2$$
$J_f$は、入力層と隠れ層の間の変換関数を微分した係数を行列化したもので、いわゆるヤコビアンである。
$J_f$の2乗をペナルティ項に加えると、特徴ベクトル場が、収縮する。これは、特徴量の不変性や頑健性につながる。
(すなわち、事前学習としての自己符号化器の学習機能向上になる。)
これを、誤差関数に加えると、次のような収縮自己符号化器の誤差関数ができあがる;
$$J_{CAE}(\theta) = \sum_{x \in D_n}(L(x,g(f(x))) + \lambda||J_f(x)||^2_F)$$
活性化関数がシグモイドの場合、上記のヤコビアンペナルティは、次のように変形できる;
$$||J_f(x)||^2_F = \sum_{i=1}^{d_h}(h_i(1-h_i))^2\sum_{j=1}^{d_x}W_{ij}^2$$
この式からわかるように、計算コストで言えば、通常の自己符号化器で、元の入力データへの再構築(reconstruction)時に誤差を計算するのと、大きく変わらない。
3. モデル適用例
事前学習器としてのCAEの性能を確かめるために、他の事前学習器との比較を行った。
・2項RBM(学習は、Contrastive Divergence)
・Basic AE
・AE + 重み減衰(wd)
・Denoising AE(ガウシアンノイズ)
・Denoising AE(二項マスキングノイズ)
自己符号化器の極値計算は、SGDでおこなった。
試験データは、CIFAR-bwとMNISTの画像分類問題をそれぞれ利用した。
トレーニングサンプル:10000
Validationサンプル:2000
テストサンプル:50000
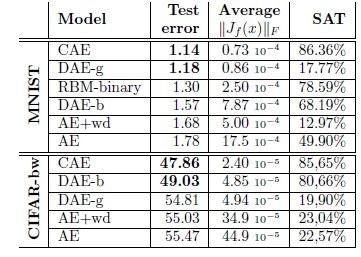
結果は下表のようになった。これより、①CAEのパフォーマンスのよさ、と②誤差率とヤコビアンペナルティ項との相関性が観測された。
積層の学習性能比較も行った。
総合的なパフォーマンスで、2層のCAEは、3層のRBMを上回った。