ETロボコンにおける自己位置計測（その２、方位計編） with EV3

方位計

方位計の概要

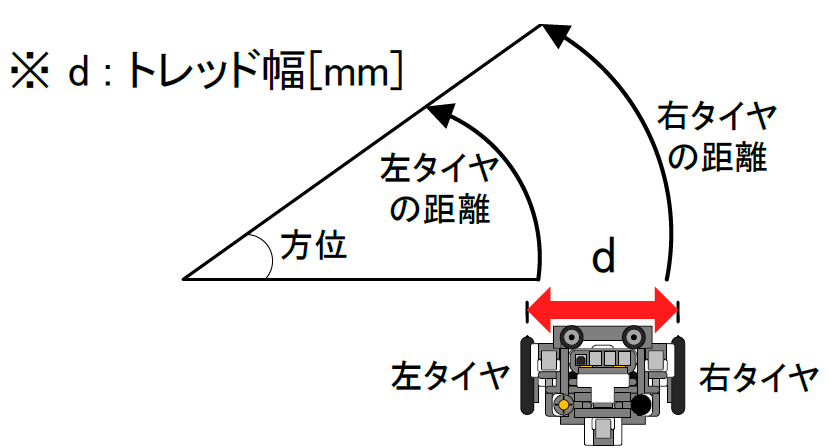
　さて、距離計に続いて今度は方位計です。これは「走行体は今、どの方向（方位）を向いているのか」を計測する計測器です。これも距離計と大体の考え方は同じですが、走行体の「全体の動き」から考えていかなければならないので、少し難しいです。以下の図のような状況を考えてみましょう。

　それでは、図のように走行体が弧を描いたように旋回して移動したと考えます。その移動の軌跡を上から眺めているとします。この時に描かれる走行体の移動軌跡の弧も「大きな円（旋回円）の一部」と考えられます。この旋回円の一部として考えたときの弧の形は、扇形になります。そして、その扇形の中心角こそが走行体の方位角度になるのです。よって、扇形の公式から方位角度は以下のようになります。

走行体の方位角度 = 360 * \frac{扇形の弧の長さ}{2 \pi * 旋回円の半径　　　　}　　　　　　　　　　　　　 (1)

　これで方位角度を出そうとすると、「扇形の弧の長さ」は走行体の移動距離となるのでいいのですが、「旋回円の半径」がちょっと厄介です。ですので、これから「旋回円の半径」がいらない形へと式を変形する手順を説明します。特に知る必要がない場合は、この欄は読み飛ばしてください。

方位計の式変形

　実際は車輪が二つあることから、この弧の軌跡によってできる旋回円は二重丸の形になります。そこで、この二つの旋回円でもって連立方程式を解くことで「旋回円の半径」を式から消すことができます。まずは、左右車輪それぞれに対しての計算式を式(1)を当てはめて考えてみましょう。

走行体の方位角度 = 360 * \frac{右タイヤの移動距離}{2 \pi * 右タイヤの旋回円の半径　　　　　　　　}　　　　　　　　(2)

走行体の方位角度 = 360 * \frac{左タイヤの移動距離}{2 \pi * 左タイヤの旋回円の半径　　　　　　　　}　　　　　　　　(3)

　この時点では、まだ「旋回円の半径」が残ってしまっています。しかし、この状況を「左側へ曲がって旋回している状況」として考えてみてください。すると、右タイヤの旋回円は二重丸の外側の円となります。これにより「右タイヤの旋回円の半径 = 左タイヤの旋回円の半径 + 走行体のトレッド幅」と読み解くことができます。よって、式(2)は以下のようになります。

走行体の方位角度 = 360 * \frac{右タイヤの移動距離}{2 \pi * (左タイヤの旋回円の半径 + 走行体のトレッド幅)　　　　　　　　　　　　　　　　}　　　(4)

　あとはこの式(4)と式(3)とで「左タイヤの旋回円の半径」が無くなるように連立方程式を解くだけです。すると、方位角度を表す式は以下の式(5)のようになります。

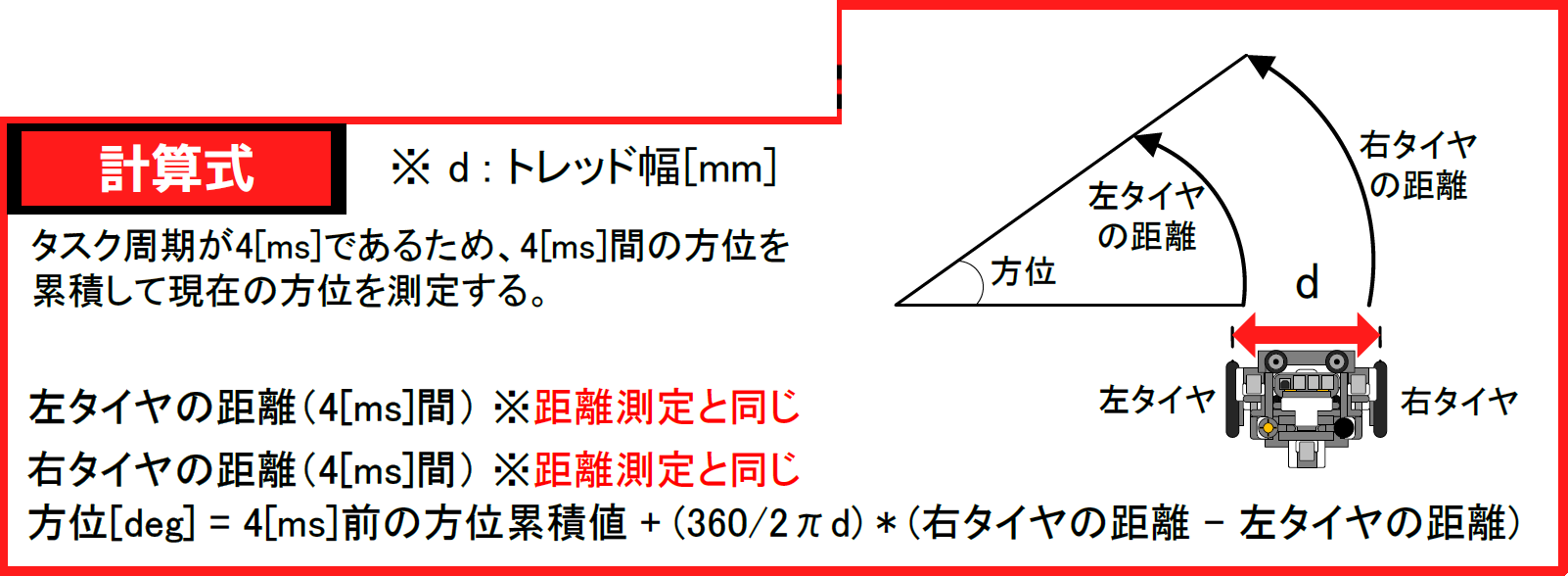
走行体の方位角度 = \frac{360}{　2 \pi * 走行体のトレッド幅　}  * (左タイヤの移動距離 - 右タイヤの移動距離)　　　　(5)

　ここでは「左側へ曲がって旋回している状況」を例に挙げて式を出しましたが、「右側に曲がって旋回している状況」でもこの式のまま使うことができます。その場合は「左タイヤの移動距離 - 右タイヤの移動距離」の部分が負の値を持ち、方位角度も負の値となります。

方位計のサンプルプログラム

　サンプルプログラムでは上記の式(5)の計算式を行っているだけです。左右車輪の走行距離は、距離計の記事※1で作成した関数を使って、左右車輪の走行距離を取得します。
※1 「ETロボコンにおける自己位置計測（その1、距離計編） with EV3」
ー http://qiita.com/PsychoGundam009/private/ba6190f08d26df7cc8ad

　この方位計においても、4ms周期で更新する関数を呼び出し、4ms間の方位の変化量を足し合わせることによって、全体の方位角度を算出しています。

Direction.c

#include "Direction.h"

#define TREAD 132.6 //車体トレッド幅(132.6mm)

static float direction = 0.0; //現在の方位

 /* 初期化 */
void Direction_init(){
	direction = 0.0;
}

 /* 方位を取得(右旋回が正転) */
float Direction_getDirection(){
	return direction;
}

/* 方位を更新 */
void Direction_update(){
	//(360 / (2 * 円周率 * 車体トレッド幅)) * (右進行距離 - 左進行距離)
	direction += (360.0 / (2.0 * PI * TREAD)) * (Distance_getDistance4msLeft() - Distance_getDistance4msRight());
}

Direction.h

#ifndef _DIRECTION_H_
#define _DIRECTION_H_

#include "parameter.h"
#include "Distance.h"

/* 初期化 */
void Direction_init();

/* 方位を取得(右旋回が正転) */
float Direction_getDirection();

 // 方位を更新
void Direction_update();

#endif

##方位計プログラムの実行例（動画）
180度旋回します。

以下が、その実行コード（一部抜粋）になります。

typedef enum {
	TURN,
	END
} RUN_STATE;

void main_task(intptr_t unused) {
	static RUN_STATE state = TURN;

	/* モーター出力ポートの設定 */
	ev3_motor_config(left_motor, LARGE_MOTOR);
	ev3_motor_config(right_motor, LARGE_MOTOR);

	/* 計測器初期化 */
	Distance_init();
	Direction_init();

	while(1) {
		/* 計測器更新 */
		Distance_update();
		Direction_update();

		switch(state) {
		case TURN:
			ev3_motor_set_power(left_motor, 30);
			ev3_motor_set_power(right_motor, -30);
			if( Direction_getDirection() > 180.0) {;
				state = END;
			}
			break;
		case END:
			ev3_motor_stop(left_motor, true);
			ev3_motor_stop(right_motor, true);
			break;
		default:
			break;
		}
	}
}