ナップサック問題の結果の図示

はじめに

「組合せ最適化を使おう」でナップサック問題の解法として、「貪欲法は良い方法である最適ではない」といいました。

実際のところ、どうなんだろうと思ったので確かめてみます。

ランダムな問題をPythonで解く

• アイテムは100個とします。
• アイテムの大きさは、(0.1, 1.0)の一様乱数とします。
• アイテムの価値は、大きさに対数正規乱数を掛けて作成します。
• ナップサックの容量を0.1刻みで変えて、繰り返し解きます。
• 結果をmatplotlibで図示します。

データの準備

python

%matplotlib inline
import math, numpy as np, matplotlib.pyplot as plt
from pulp import *
np.random.seed(1)
n = 100 # アイテム数
siz = np.random.uniform(0.1, 1.0, n)
prf = siz * np.random.lognormal(1, 0.1, n)
eff = prf / siz
siz, prf, eff = np.array([siz, prf, eff]).T[eff.argsort()].T
r1, r2, p1, p2 = [], [], [], []

近似解法(貪欲法)の結果

貪欲法では、効率(価値/大きさ)の良い順に調べていき、容量を超過しないように入れていきます。

python

for sz in range(math.ceil(sum(siz)*10)):
    v, r, rm = 0, [], sz / 10
    for i in range(len(siz)-1, -1, -1):
        r.append(int(rm < siz[i]))
        if r[-1] == 0:
            rm -= siz[i]
            v += prf[i]
    r1.append(list(reversed(r)))
    p1.append(v)
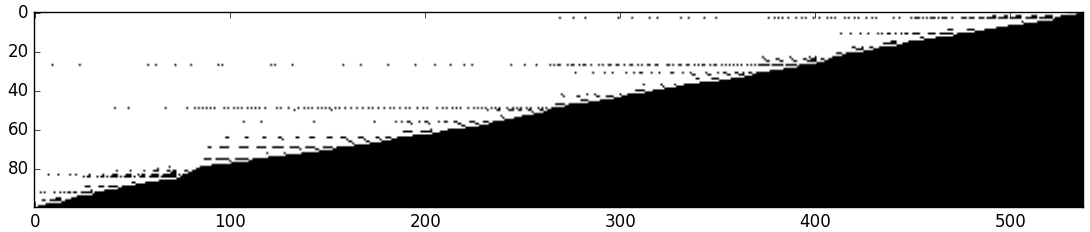
plt.imshow(np.array(r1).T, cmap='gray')

• 538回解いて 数ミリ秒でした。
• 縦は効率の良い順のアイテムに対応します。横は、ナップサックの容量×10に対応します。
• 黒が選択したアイテム、白が選択されなかったアイテムを表します。
• 貪欲法は、効率の良い順に詰めるので、比較的境界がはっきりします。

厳密解法の結果

pulpで混合整数最適化問題として解いてみましょう。

python

m = LpProblem(sense=LpMaximize)
v = [LpVariable('v%d'%i, cat=LpBinary) for i in range(len(siz))]
m += lpDot(prf, v)
e = lpDot(siz, v) <= 1
m += e
r = []
for sz in range(math.ceil(sum(siz)*10)):
    e.changeRHS(sz / 10)
    m.solve()
    r2.append([1 - int(value(x)) for x in v])
    p2.append(value(m.objective))
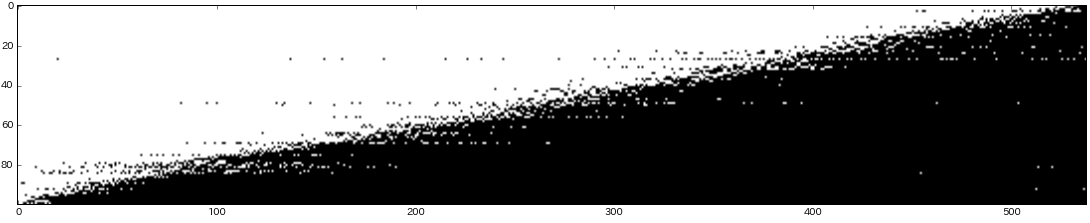
plt.imshow(np.array(r2).T, cmap='gray')

• 538回解いて Gurobi 6.5.1で16秒、デフォルトのCBCでは58秒でした。
• 境界付近で白と黒が混じっているのは、効率的でないものを選んだ方が全体として最適であることをあらわしています。

貪欲法の精度

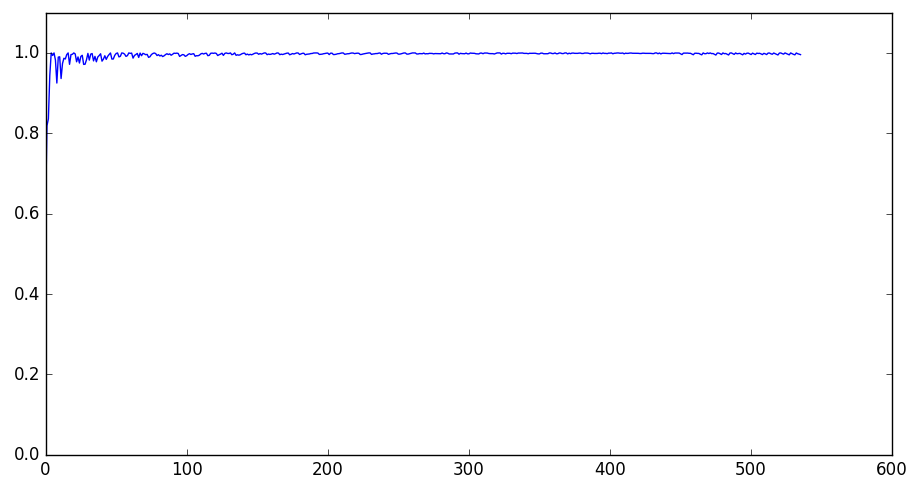
貪欲法の解の値を厳密解の値で割ったものをグラフ化します。縦が比で、横がナップサックの容量×10です。

python

plt.ylim((0, 1.1))
plt.plot(np.array(p1[2:]) / np.array(p2[2:]))

容量が小さくて、入るアイテム数が少ないと、多少、誤差がありますが、ある程度のアイテム数があれば、かなり精度がよいことがわかります。

追記(吝嗇法(stingy method))

H22.Math.Prog.No.9.pdfにあった吝嗇法を試してみました。

python

r3,p3 = [],[]
for sz in range(math.ceil(sum(siz)*10)):
    v, r, ca, rm = 0, [], sz / 10, sum(siz)
    for i in range(len(siz)):
        r.append(int(not(0 < rm-siz[i] <= ca and siz[i] <= ca)))
        rm -= siz[i]
        if r[-1] == 0:
            ca -= siz[i]
            v += prf[i]
    r3.append(r)
    p3.append(v)
plt.imshow(np.array(r3).T, cmap='gray');

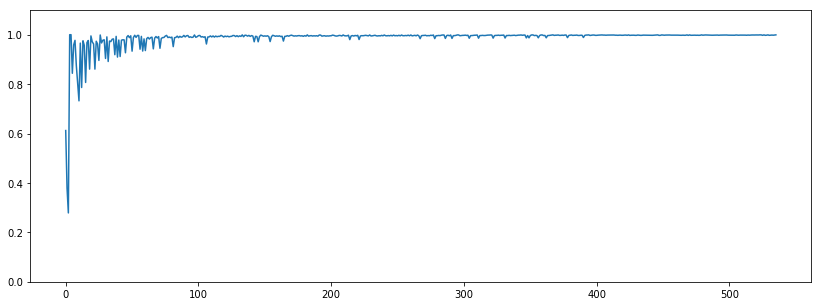
貪欲法は、境界の上にはみ出ていましたが、吝嗇法は境界の下に抜けがあるのがわかります。
性能を見てみると、貪欲法より悪い感じです。

python

plt.ylim((0, 1.1))
plt.plot(np.array(p3[2:]) / np.array(p2[2:]));

以上