やること
- 動的最適化の簡単な確認
- ゴルフの期待値の計算
動的最適化の簡単な確認
動的最適化とは
- 動的最適化(Dynamic Optimization)とは、動的計画法(Dynamic Programming)の最近のよび方です。
- 部分問題を解き、その結果を利用して、問題全体を解きます。そのとき、繰返し あらわれる同じ部分問題に対して、結果のキャッシュを使って効率よく計算します(メモ化)。
ナップサック問題で簡単な確認
Pythonでは、lru_cacheを使うと簡単に結果をキャッシュできます。(引数がハッシュ化可能な場合)
ナップサック問題で効果を見てみましょう。
python
%matplotlib inline
import numpy as np, matplotlib.pyplot as plt
from functools import lru_cache
plt.rcParams['font.family'] = 'IPAexGothic'
plt.rcParams['font.size'] = 16
count = 0
np.random.seed(1)
_size = np.random.randint(100, 200, 100)
_weight = np.random.randint(100, 200, 100)
def make_sample(n):
size = tuple(_size[:n])
weight = tuple(_weight[:n])
capacity = sum(size) // 3 * 2
return size, weight, capacity
def knapsack1(size, weight, capacity):
if len(size) == 0 or capacity < min(size):
return 0
global count
count += 1
r = capacity - size[0]
if r < 0:
return knapsack1(size[1:], weight[1:], capacity)
else:
return max(weight[0] + knapsack1(size[1:], weight[1:], r),
knapsack1(size[1:], weight[1:], capacity))
@lru_cache(None)
def knapsack2(size, weight, capacity):
if len(size) == 0 or capacity < min(size):
return 0
global count
count += 1
r = capacity - size[0]
if r < 0:
return knapsack2(size[1:], weight[1:], capacity)
else:
return max(weight[0] + knapsack2(size[1:], weight[1:], r),
knapsack2(size[1:], weight[1:], capacity))
def count_knapsack1(n):
global count
count = 0
knapsack1(*make_sample(n))
return count
def count_knapsack2(n):
global count
count = 0
knapsack2(*make_sample(n))
return count
ここでは、ナップサック問題を最初のアイテムを選ぶか選ばないかで部分問題に分けて、再帰的に解きます。
- count_knapsack1がキャッシュなしの呼出し回数を計算します。
- count_knapsack2がキャッシュありの呼出し回数を計算します。
違いは、lru_cacheの有無だけです。結果を見てみましょう。
python
rng = [10, 12, 14, 16, 18, 20]
res1 = [count_knapsack1(i) for i in rng]
res2 = [count_knapsack2(i) for i in rng]
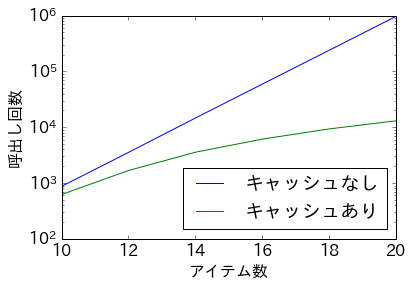
plt.plot(rng, res1, label='キャッシュなし')
plt.plot(rng, res2, label='キャッシュあり')
plt.xlabel('アイテム数')
plt.ylabel('呼出し回数')
plt.yscale('log')
plt.legend(loc='lower right');
縦軸は対数軸なので、キャッシュにより、かなり高速化されているのがわかります。
ゴルフの期待値の計算
次に、簡単なゴルフの問題を考えてみます。
- 自分と相手の2人で18ホールのスコアを競います。勝てば+1点、負ければ―1点、引き分けは0点とします。
- 18ホールですが、全て同じ条件とします。
- 相手は、20%の確率でボギー、60%の確率でパー、20%の確率でバーディーになります。
- 自分は、各ホールごとに、安全策と強硬策のどちらかを必ず選ぶものとします。
- 安全策は、10%の確率でボギー、80%の確率でパー、10%の確率でバーディーになります。
- 強硬策は、30%の確率でボギー、40%の確率でパー、30%の確率でバーディーになります。
策ごとの可能性(%)を表にしてみましょう。
| 安全策 | 強硬策 | |||||||
| 相\自 | +1 | 0 | -1 | 相\自 | +1 | 0 | -1 | |
| +1 | 2 | 16 | 2 | +1 | 6 | 8 | 6 | |
| 0 | 6 | 48 | 6 | +0 | 18 | 24 | 18 | |
| -1 | 2 | 16 | 2 | -1 | 6 | 8 | 6 | |
スコア差でみると[-2, -1, 0, +1, +2]の5通りです。
部分問題は、この10通り(安全策5通り+強硬策5通り)を場合分けして作ります。
python
a0 = np.arange(-2, 3)
a1 = [0.02, 0.22, 0.52, 0.22, 0.02]
a2 = [0.06, 0.26, 0.36, 0.26, 0.06]
@lru_cache(None)
def golf(rem, df):
"""
rem: 残りホール数
df: 現在のスコア差(負が勝ち)
返り値: 安全策を取るかどうか, 得点期待値
"""
if rem == 1: # 最終ホール
s1 = np.inner(a1, (a0+df)<0) - np.inner(a1, (a0+df)>0)
s2 = np.inner(a2, (a0+df)<0) - np.inner(a2, (a0+df)>0)
else:
a = [golf(rem-1, df+i)[1] for i in a0]
s1 = np.inner(a, a1)
s2 = np.inner(a, a2)
return s1 >= s2, max(s1, s2)
rng = range(18,0,-1)
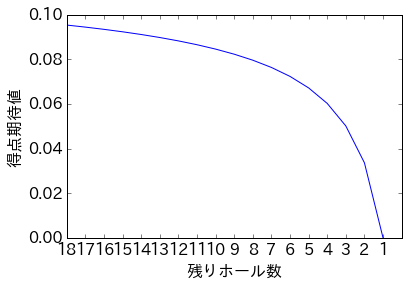
plt.xlabel('残りホール数')
plt.ylabel('得点期待値')
plt.plot(range(18), [golf(i, 0)[1] for i in rng]);
plt.xticks(range(18), rng);
残りホール数が多いほど、自分の得点期待値が高いです。これは、有利な場合は安全策、不利な場合は強硬策を取れるためと考えられます。
以上