重みマッチング問題における解法の比較

これなに

最大重みマッチング問題の2つの解法の計算時間を比較した。

計算

python

import time, numpy as np, networkx as nx
from pulp import *
from ortoolpy import addbinvars
np.random.seed(1)
平均次数 = 3
for N in [10,100,200,500,1000,2000,5000]:
    # グラフ作成
    g = nx.fast_gnp_random_graph(N, 平均次数/(N-1))
    for r,(i,j) in zip(np.random.rand(g.number_of_edges()),g.edges_iter()):
        g.edge[i][j]['weight'] = r

    # 汎用ソルバ(cbc)で計算
    m = LpProblem(sense=LpMaximize)
    x = addbinvars(g.number_of_edges())
    for v,(i,j) in zip(x, g.edges()):
        g[i][j]['Var'] = v
    m += lpDot([g[i][j]['weight'] for i,j in g.edges()], x)
    for nd in g.nodes():
        m += lpSum(d['Var'] for d in g[nd].values()) <= 1
    t1s = time.clock()
    m.solve()
    n1 = len([i for i,v in enumerate(x) if value(v) > 0.5])
    t1e = time.clock()

    # エドモンズ法
    t2s = time.clock()
    n2 = len(nx.max_weight_matching(g))//2
    t2e = time.clock()
    assert n1==n2
    print(N,t1e-t1s,t2e-t2s)
>>>
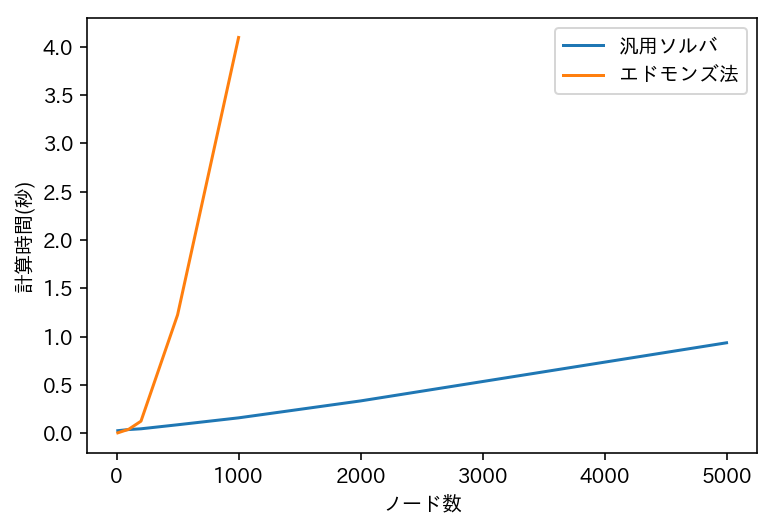
10 0.02683257321768906 0.004652122559491545
100 0.038709433923941106 0.041949099861085415
200 0.046430152317043394 0.1253287561412435
500 0.08796162778162397 1.2250798634777311
1000 0.15964821091620252 4.0942329679674
2000 0.3348240090563195 20.510134776166524
5000 0.9361551560868975 159.31649612302135

可視化

jupyter

%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'IPAexGothic'
plt.xlabel('ノード数')
plt.ylabel('計算時間(秒)')
plt.plot([10,100,200,500,1000,2000,5000],[0.0268,0.0387,0.0464,0.0879,0.1596,0.3348,0.9361], label='汎用ソルバ')
plt.plot([10,100,200,500,1000],[0.0046,0.0419,0.1253,1.2250,4.0942], label='エドモンズ法')
plt.legend();

考察

• 一般的に専用ソルバの方が汎用ソルバより性能がよいと期待される。(ノーフリーランチ定理 - Wikipedia)
• 両者ともに厳密解を求めている。
• 汎用ソルバのデフォルトは無料のcbcである。
• 汎用ソルバは、分枝限定法をベースにした、多項式オーダを保証していない方法であるが、計算時間が線形オーダに近く、5000ノードでも1秒かからない。
• 専用アルゴリズムであるエドモンズ法は、効率のよい方法と言われているが、計算時間が線形オーダになっていないので、5000ノードでは汎用ソルバの 170 倍になっている。

以上