数理モデルにおける変数の和

これなに

最適化の数理モデル作成時の変数の和の書き方

C# や Java において、文字列の連結で StringBuilder を使うべきなのと同様に、数理モデルの変数の加算でも、同様のテクニックがあります。

表にまとめます。

パッケージ	書き方	可否
-	sum	×
Python-MIP	xsum	○
PuLP	lpSum	○
PuLP	lpDot	○
GUROBI	quicksum	○

xsumやquicksumで合計や内積を計算できます。

可否が"○"のものは線形オーダーですが、"×"のものは2乗のオーダーになります。

確認

PuLPで確認してみましょう。

python3

from pulp import LpVariable, value
for i in [1000, 2000, 5000]:
    v = [LpVariable('v%d'%i) for i in range(i)]
    print(i)
    %timeit lpSum(v)
    %timeit sum(v)
>>>
1000
1000 loops, best of 3: 1.44 ms per loop
1 loop, best of 3: 403 ms per loop
2000
100 loops, best of 3: 2.89 ms per loop
1 loop, best of 3: 1.58 s per loop
5000
100 loops, best of 3: 7.11 ms per loop
1 loop, best of 3: 10 s per loop

以上

---

参考

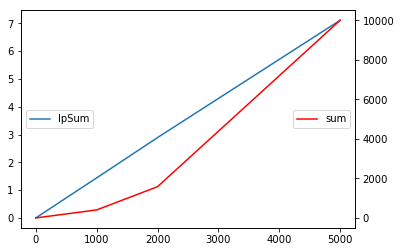
• グラフ描画

python3

import matplotlib.pyplot as plt
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()
ax1.plot([0,1000,2000,5000], [0,1.44,2.89,7.11], label='lpSum')
ax2.plot([0,1000,2000,5000], [0,403,1580,10000], label='sum', color='red')
ax1.legend(loc='center left')
ax2.legend(loc='center right');