組合せ最適化で、ゲームのグループ分け

これなに

あなたは、結婚式の2次会の幹事です。
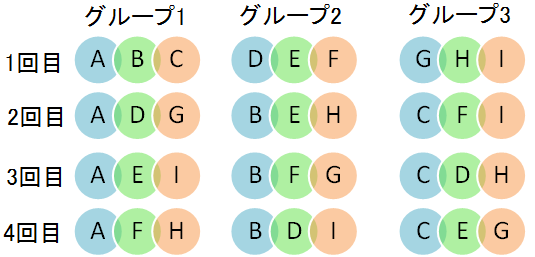
9人の参加者が、3人ずつ3つのグループに分かれてゲームをします。
このゲームは4回行われます。
どの2人も、同じグループになるのが1回までになるようグループ分けを考えましょう。

※ LocalSolver例題集のSocial golferをヒントにしています。

定式化 ＆ Python

組合せ最適化を使って解きましょう。例によって、PuLPとpandasを使います。
「誰が、いつ、どのグループか」が成立するかを 0-1 変数 Varで表します。

python3

import pandas as pd
from pulp import *
from ortoolpy import addvars, addbinvars
from itertools import permutations
uss = [chr(65+i) for i in range(9)] # Users
a = pd.DataFrame([(us,wk,gr) for us in uss for wk in range(4)
        for gr in range(3)], columns=['User','Time','Group'])
a['Var'] = addbinvars(len(a)) # 変数
a[:3] # 先頭の3行表示

	User	Time	Group	Var
0	A	0	0	v0001
1	A	0	1	v0002
2	A	0	2	v0003

定式化

目的関数	なし
制約	各人各回で1つのグループに所属
1グループは3人
どの2人も、同一グループになる回数は1回まで (同一のグループのとき1になる変数を使う)

python3

m = LpProblem() # 数理モデル
for _,v in a.groupby(['User','Time']):
    m += lpSum(v.Var) == 1 # 各人各回で1つのグループに所属
for _,v in a.groupby(['Time','Group']):
    m += lpSum(v.Var) == 3 # 1グループは3人
for uu in permutations(uss,2):
    y = addvars(4*3) # 同一のグループのとき1になる変数
    m += lpSum(y) <= 1 # どの2人も、同一グループになる回数は1回まで
    for w,(_,v) in zip(y, a[a.User.isin(uu)].groupby(['Time','Group'])):
        m += lpSum(v.Var) <= 1+w # yとVarの関係
m.solve()
a['Val'] = a.Var.apply(value)
a[a.Val>0].groupby(['Time','Group']).User.sum() # 結果表示

結果

Time  Group
0     0        AFI
      1        EGH
      2        BCD
1     0        ABH
      1        CEF
      2        DGI
2     0        ACG
      1        BEI
      2        DFH
3     0        BFG
      1        ADE
      2        CHI

補足 - その1

素直に定式化すると、目的関数が2次の非線形最適化になります。そのままでは、MIPソルバでは解けないので、ペアごとに新たな変数(y)を追加することで（変数は多くなりますが）線形最適化になります。
とはいえ、規模が大きい場合は、局所探索法などの近似解法の方が有効かもしれません。

補足 - その2

• PuLP の LpProblem は、問題ではなく、モデルです！

  • 問題：解決したいと思っていること
  • モデル：コンピュータで扱えるように表現されたもの

• 結果を見直すときに変えるのは、問題ではなくモデル！

以上